Навигация
МНОЖЕННЯ ЧИСЕЛ, ЩО ПРЕДСТАВЛЕНІ В ФОРМІ З ФІКСОВАНОЮ КОМОЮ
3.2. МНОЖЕННЯ ЧИСЕЛ, ЩО ПРЕДСТАВЛЕНІ В ФОРМІ З ФІКСОВАНОЮ КОМОЮ
3.2.1. Прості методи множення
Нехай ![]() - модуль множеного,
- модуль множеного, ![]() - модуль множника. Тоді, у разі представлення чисел у формi з фіксованою комою, модуль добутку
- модуль множника. Тоді, у разі представлення чисел у формi з фіксованою комою, модуль добутку ![]() визначається за формулою:
визначається за формулою:
 . (3.1)
. (3.1)
Звідси випливає, що процес множення полягає у нагромадженні часткових добутків ![]() , яким керують цифри множника
, яким керують цифри множника ![]() . Керування процесом множення може починатись як з молодших розрядів множнику, так і зі старших.
. Керування процесом множення може починатись як з молодших розрядів множнику, так і зі старших.
З урахуванням цього розглянемо прості методи множення.
Метод 1. Перетворимо формулу (3.1) до такого вигляду:
![]() .
.
Звідси випливає, що множення зводиться до п-кратного виконання циклу:
![]() ,
,
де ![]() ,
,
для початкових значень
![]() .
.
Це означає, що множення починається з молодших розрядiв множника ![]() i множене зсувається вліво на один розряд
i множене зсувається вліво на один розряд ![]() в кожному циклi. При цьому до суми часткових добутків
в кожному циклi. При цьому до суми часткових добутків ![]() додається або зсунене множене, якщо
додається або зсунене множене, якщо ![]() =1, або нуль, коли
=1, або нуль, коли ![]() =0. Після завершення п-го циклу утворюється остаточний результат множення. Тобто
=0. Після завершення п-го циклу утворюється остаточний результат множення. Тобто
![]() .
.
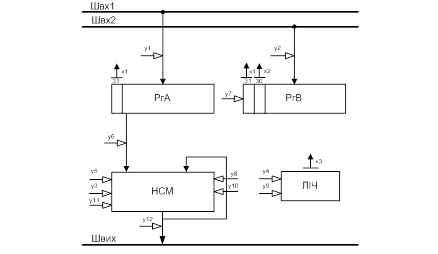
Реалізація даного методу вимагає (рис. 3.1) 2п-розрядного зсувового регістру множеного РгА, п-розрядного зсувового регістру множнику РгВ, 2п схем І, що пропускають код із виходу регістра РгА на вхід 2п-розрядного нагромаджувального суматора НСМ коли ![]() =1 і забороняють його надходження коли
=1 і забороняють його надходження коли ![]() =0. Тут чергова цифра множника, що керує додаванням часткових добутків, береться з молодшого розряду регістра множника.
=0. Тут чергова цифра множника, що керує додаванням часткових добутків, береться з молодшого розряду регістра множника.
Оскільки зсув кодів у регістрах РгА і РгВ може виконуватись одночасно з додаванням у нагромаджувальному суматорі НСМ, то час множення п-розрядних кодів за даним методом дорівнює:
![]() . (3.2)
. (3.2)
Тут ураховано те, що в машинах завжди час додавання ![]() більше, ніж час зсуву коду
більше, ніж час зсуву коду ![]() .
.
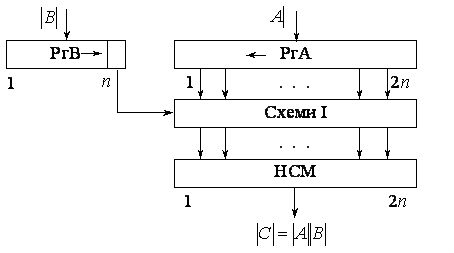
Рис. 3.1. Структурна схема пристрою, що реалізує множення за методом 1
Приклад 3.2. Помножити числа А = - 0, 10100 і В = 0, 10011, використовуючи метод 1.
Розв'язання. Для даних чисел маємо: ![]() =1;
=1; ![]() = 0, 10100;
= 0, 10100; ![]() =0;
=0; ![]() = 0, 10011. Визначаємо знак добутку:
= 0, 10011. Визначаємо знак добутку: ![]() =1
=1![]() 0=1.
0=1.
Усі дії, що виконуються в кожному циклі множення, зручно подати у вигляді таблиці (табл. 3.2).
Відповідь: С= - 0, 0101111100.
Метод 2. Представимо (3.1) у вигляді:
![]() .
.
Обчислення добутку за цією формулою зводиться до п-кратного виконання циклу:
![]() ;
;
![]()
для початкових значень
![]() .
.
Звідси випливає, що множення починається зі старших розрядiв множника ![]() i множене зсувається вправо на один розряд
i множене зсувається вправо на один розряд ![]() в кожному циклi. При цьому до суми часткових добутків
в кожному циклi. При цьому до суми часткових добутків ![]() додається або зсунене множене, якщо
додається або зсунене множене, якщо ![]() =1, або нуль, коли
=1, або нуль, коли ![]() =0. Після завершення п-го циклу утворюється остаточний результат множення
=0. Після завершення п-го циклу утворюється остаточний результат множення ![]() .
.
Таблиця 3.2 - Приклад множення за методом 1

Для реалізації даного методу множення потрібні (рис.3.2) 2п-розрядний регістр множеного РгА з колами для зсуву вправо, п-розрядний регістр множника РгВ з колами для зсуву вліво, 2п схем І і 2п-розрядний нагромаджувальний суматор НСМ. Тут чергова цифра множника, що керує додаванням часткових добутків, береться зі старшого розряду регістра множника.
Час множення за даним методом дорівнює:
![]() . (3.3)
. (3.3)
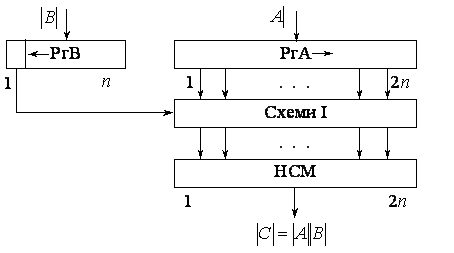
Рис. 3.2. Структурна схема пристрою, що реалізує множення за методом 2
Приклад 3.3. Помножити числа А = - 0, 10100 і В = - 0, 10011, використовуючи метод 2.
Розв'язання. Для даних чисел маємо: ![]() =1;
=1; ![]() = 0, 10100;
= 0, 10100; ![]() =1;
=1; ![]() = 0, 10011. Визначаємо знак добутку:
= 0, 10011. Визначаємо знак добутку: ![]() =1
=1![]() 1=0. Усі дії, що виконуються під час множення, наведені у табл. 3.3.
1=0. Усі дії, що виконуються під час множення, наведені у табл. 3.3.
Відповідь: С= 0, 0101111100.
Метод 3. Перетворимо (3.1) за схемою Горнера для обчислення поліномів:
![]() =
=
=![]() .
.
Звідси випливає, що множення зводиться до п-кратного виконання циклу:
![]() для початкових значень
для початкових значень ![]() .
.
Таблиця 3.3 - Приклад множення за методом 2

У кожному циклі до суми часткових добутків ![]() додається або множене, якщо
додається або множене, якщо ![]() =1, або нуль, коли
=1, або нуль, коли ![]() =0, після чого сума часткових добутків помножується на
=0, після чого сума часткових добутків помножується на ![]() , тобто зсувається на один розряд управо. Після завершення п-го циклу утворюється остаточний результат множення
, тобто зсувається на один розряд управо. Після завершення п-го циклу утворюється остаточний результат множення ![]() . Звідси випливає, що множення починається з молодших розрядiв множника
. Звідси випливає, що множення починається з молодших розрядiв множника ![]() i зсувається сума часткових добутків управо на один розряд в кожному циклi.
i зсувається сума часткових добутків управо на один розряд в кожному циклi.
Для реалізації даного методу множення потрібні (рис.3.3) п-розрядний регістр множеного РгА, п-розрядний регістр множника РгВ з колами для зсуву вліво, п схем І і (2п+1)-розрядний нагромаджувальний суматор НСМ з колами для зсуву вправо. Тут множене завжди додається до п старших розрядів суми часткових добутків. Один додатковий розряд ліворуч у НСМ необхідний для запам'ятовування цифри переповнення, що може виникнути в процесі додавання; під час наступного зсуву ця цифра піде в старший з основних розрядів нагромаджувального суматора, так що в остаточному результаті переповнення не буде.
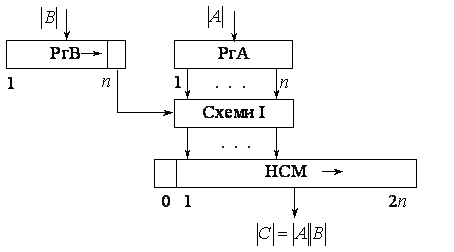
Рис. 3.3. Структурна схема пристрою, що реалізує множення за методом 3
Оскільки в кожному циклі в нагромаджувальному суматорі НСМ спочатку виконується додавання, а потім зсув коду, то час множення п-розрядних кодів за даним методом дорівнює:
![]() . (3.4)
. (3.4)
Приклад 3.4. Помножити числа А = 0, 11100 і В = 0, 10011, використовуючи метод 3.
Розв'язання. Для даних чисел маємо: ![]() =0;
=0; ![]() = 0, 11100;
= 0, 11100; ![]() =0;
=0; ![]() = 0, 10011. Визначаємо знак добутку:
= 0, 10011. Визначаємо знак добутку: ![]() =0
=0![]() 0=0. Послідовність дій, що виконуються для одержання модулю добутку, показано в табл. 3.4.
0=0. Послідовність дій, що виконуються для одержання модулю добутку, показано в табл. 3.4.
Таблиця 3.4 - Приклад множення за методом 3
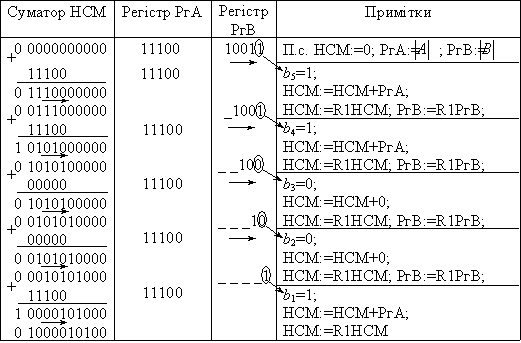
Відповідь: С= 0,1000010100.
Особливість даного методу множення полягає в тому, що в кожному циклі визначається одна вірогідна цифра добутку (починаючи з наймолодшого розряду), яка не змінюється в інших циклах множення. Врахування цього дозволяє зменшити кількість розрядів нагромаджувального суматора вдвічі, обчислюючи 2п-розрядний добуток. При цьому для зберігання вірогідних цифр використовуються розряди регістра множника, що звільняються в процесі множення. Структурна схема такого пристрою для множення наведена на рис. 3.4. Тут вихід молодшого розряду нагромаджувального суматора НСМ з'єднаний з входом старшого розряду регістра множника РгВ. Цим самим утворюється спільний зсувовий регістр. Старші розряди добутку формуються в НСМ, а молодші в РгВ.
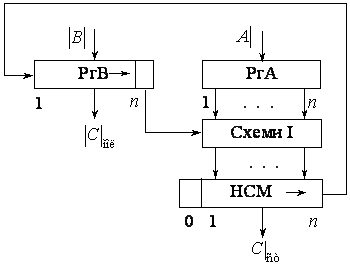
Рис. 3.4. Структурна схема модифікованого пристрою, що реалізує множення за методом 3
Приклад 3.5. Описати множення чисел А = 0, 11100 і В = 0, 10011, що реалізується модифікованим пристроєм.
Розв'язання. Для даних чисел маємо: ![]() =0;
=0; ![]() = 0, 11100;
= 0, 11100; ![]() =0;
=0; ![]() = 0, 10011. Визначаємо знак добутку:
= 0, 10011. Визначаємо знак добутку: ![]() =0
=0![]() 0=0. Послідовність дій, виконуваних у процесі множення, наведено в табл. 3.5.
0=0. Послідовність дій, виконуваних у процесі множення, наведено в табл. 3.5.
Відповідь: С= 0,1000010100.
Метод 4. Якщо перетворити (3.1) за схемою Горнера до вигляду:
![]() ,
,
то множення зведеться до п-кратного виконання циклу:
![]()
для початкових значень ![]() .
.
У кожному циклі до суми часткових добутків ![]() додається або множене, якщо
додається або множене, якщо ![]() =1, або нуль, коли
=1, або нуль, коли ![]() =0, після чого сума часткових добутків зсувається на один розряд вліво. Тобто множення починається зі старших розрядiв множника
=0, після чого сума часткових добутків зсувається на один розряд вліво. Тобто множення починається зі старших розрядiв множника ![]() i зсувається сума часткових добутків вліво на один розряд в кожному циклi.
i зсувається сума часткових добутків вліво на один розряд в кожному циклi.
Таблиця 3.5 - Приклад множення з використанням модифікованого пристрою

Для реалізації даного методу множення потрібні (рис.3.5) п-розрядний регістр множеного РгА, п-розрядний регістр множника РгВ з колами для зсуву вліво, п схем І і 2п-розрядний нагромаджувальний суматор НСМ з колами для зсуву вліво. Тут множене завжди додається до п молодших розрядів суми часткових добутків.
Враховуючи те, що в кожному циклі в нагромаджувальному суматорі НСМ спочатку виконується додавання, а потім зсув коду, маємо такий час множення п-розрядних кодів за даним методом:
![]() . (3.5)
. (3.5)
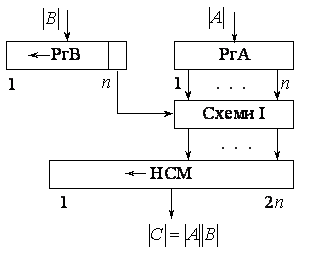
Рис. 3.5. Структурна схема пристрою, що реалізує множення за методом 4
Приклад 3.6. Помножити числа А = 0, 10100 і В = 0, 10011, використовуючи метод 4.
Розв'язання. Для даних чисел маємо: ![]() =0;
=0; ![]() = 0, 10100;
= 0, 10100; ![]() =0;
=0; ![]() = 0, 10011. Визначаємо знак добутку:
= 0, 10011. Визначаємо знак добутку: ![]() =0
=0![]() 0=0. Послідовність дій, виконуваних у процесі множення, наведено у табл. 3.6.
0=0. Послідовність дій, виконуваних у процесі множення, наведено у табл. 3.6.
Відповідь: С= 0, 0101111100.
Аналіз описаних методів множення і пристроїв, що їх реалізують показує таке.
Тривалість процесу множення за першим і другим методами менше, ніж за третім і четвертим, за рахунок суміщення у часі операцій додавання часткових добутків і зсувів множеного.
За кількістю апаратури перевагу варто віддати модифікованому пристрою, що реалізує третій метод множення.
Пристрій, що реалізує перший метод множення виявляється дуже не ощадливим за кількістю необхідної апаратури. Крім того, розряди суматора НСМ використовуються неефективно: у початкових циклах множення старші розряди зайняті увесь час "додаванням" нулів, наприкінці множення на молодші розряди надходять з регістра РгА нулі, тобто ніяких корисних операцій вони фактично не роблять.
Таблиця 3.6 - Приклад множення за методом 4

У той же час цей пристрій є вигідним з такої точки зору. До початку множення можна записати в суматор НСМ замість нуля яке-небудь інше число ![]() (скажемо, результат попереднього множення). Тоді в результаті множення можна одержати у суматорі НСМ замість добутку
(скажемо, результат попереднього множення). Тоді в результаті множення можна одержати у суматорі НСМ замість добутку ![]() значення суми
значення суми ![]() +
+![]() . Це дозволяє легко організувати нагромадження суми парних добутків чисел
. Це дозволяє легко організувати нагромадження суми парних добутків чисел ![]() . У модифікованому пристрої, що реалізує третій метод, цього зробити не можна, тому що в процесі множення початковий вміст суматора НСМ зсувається п раз управо.
. У модифікованому пристрої, що реалізує третій метод, цього зробити не можна, тому що в процесі множення початковий вміст суматора НСМ зсувається п раз управо.
На підставі вищевикладеного можна вважати найбільш зручними для застосування в ЦОМ пристрої, які реалізують перший і третій методи множення, що і підтверджується практикою розробки обчислювальних пристроїв.
Похожие работы
... автомата повинна містити певну кількість логічний елементів, що утворюють функціонально повну систему для синтезу необхідної комбінаційної схеми. 1.5 Контроль виконання арифметичних операцій Арифметичні операції виконуються на суматорах прямого, оберненого і доповняльного коду. Припустимо, що зображення чисел зберігаються в машині в деякому коді, тобто операція перетворення в заданий код або ...
... в іншу (найчастіше для переведення із двійкової, вісімкової та шістнадцяткової систем числення у десяткову, і навпаки). 6. Програмна реалізація Програма розроблена для перетворення чисел з однієї системи числення в іншу.Реалізована в середовищі програмування Borland C++Builder. Лістінг програми: #include <vcl.h> #pragma hdrstop #include "Unit1.h" #include <math.h> #include < ...
... льш прості операції які називаються мікроопераціями тобто кожна операція – це визначена послідовність мікрооперацій. Існують два основні типи керуючих автоматів 1. Керуючий автомат з жорсткою чи схемною логікою. Для кожної операції будується набір комбінаційних схем які в потрібних тактах збуджують відповідні керуючі сигнали. Іншими словами ...
... тову складність операцій у полі, то можна оцінити результуючу бітову складність операцій з многочленами. Щоб відрізняти арифметичну складність від бітової в оцінках ми використовуватимемо символи і . Обчислення значень многочленів. Нехай – довільне кільце. Розглянемо добре відомий алгоритм Руфіні - Горнера для обчислення значень многочлена над кільцем у точці. Останнє число ,і буде шуканим ...



0 комментариев