Навигация
2. Признак Коши
Теорема 2 (признак Коши). Пусть дан ряд
![]() ,
, ![]() . (1)
. (1)
Если существует конечный предел
![]() ,
,
то 1) при ![]() ряд сходится;2) при
ряд сходится;2) при ![]() ряд расходится.
ряд расходится.
◄ 1) Пусть ![]() . Возьмем число q такое, что
. Возьмем число q такое, что ![]() . Так как существует предел
. Так как существует предел
![]() ,
,![]()
где ![]() , то, начиная с некоторого номера N , будет выполняться неравенство
, то, начиная с некоторого номера N , будет выполняться неравенство ![]() .
.
В самом деле, из определенного равенства вытекает, что для любого ε ,в том числе и для
ε = ![]() , найдется такой номер N , начиная с которого будет выполняться неравенство
, найдется такой номер N , начиная с которого будет выполняться неравенство
![]() ,
,
откуда ![]()
![]()
![]() или что тоже,
или что тоже,
![]() .
.
Отсюда получаем
![]() для
для ![]() .
.
Таким образом, все члены ряда, начиная с ![]() , меньше соответствующих членов сходящегося ряда
, меньше соответствующих членов сходящегося ряда ![]() . По признаку сравнения ряд
. По признаку сравнения ряд
![]()
![]()
сходится, а значит сходится и ряд(1).
2)Пусть ![]() . Тогда, начиная с некоторого номера N для всех n > N , будет выполняться неравенство
. Тогда, начиная с некоторого номера N для всех n > N , будет выполняться неравенство ![]() , или
, или
![]() .
.
Следовательно,
![]()
И ряд (1) расходится. ►
Замечание. Если ![]() , то ряд (1) может как сходиться, так и расходиться.
, то ряд (1) может как сходиться, так и расходиться.
Примеры. Исследовать на сходимость следующие ряды:
1.
![]() .
.
◄ Имеем
![]() ,
, ![]() ;
;
![]()
![]() .
.
Ряд сходится. ►
2. 
◄ Здесь
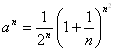 ,
, ![]() ;
;
![]()

Ряд сходится. ►
3. Интегральный признак сходимости ряда
Теорема 3 (интегральный признак сходимости). Пусть функция f(x) определена, непрерывна, положительна и не возрастает на луче ![]() . Тогда:
. Тогда:
1) числовой ряд ![]() сходится, если сходится несобственный интеграл
сходится, если сходится несобственный интеграл
![]() ;
(1)
;
(1)
2) ряд ![]() расходится, если расходится несобственный интеграл (1)
расходится, если расходится несобственный интеграл (1)
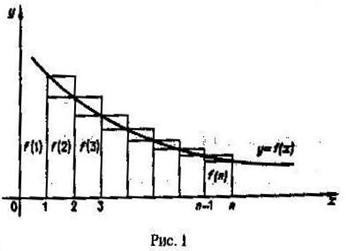
◄ Возьмем на графике функции f(x) точки с абсциссами
x1=1, x2=2, x3=3, … , xn = n
и построим две ступенчатые фигуры, состоящие из выступающих и входящих прямоугольников так, как показано рис. 1. Площадь Q криволинейной трапеции, ограниченной прямыми x = 1, x = n, y=0 и кривой y = f(x) равна
![]() .
.
Возьмем n-ю частичную сумму ряда ![]() :
:
S n = f(1) + f(2) + f(3) + … + f(n) ,
Тогда площадь Q+ выступающей фигуры будет равна
Q+= f(1) + f(2) + f(3) + … + f(n-1) = S n-1
А площадь Q- входящей фигуры равна
Q- = + f(2) + f(3) + … + f(n) = S n - f(1).
Из построения и свойств функции f(x) следует, что
Q- < Q < Q+ , т.е.
S n - f(1) < ![]() < S n-1.
< S n-1.
Так как S n-1 < S n
(в силу условия ![]() ), то
), то
S n - f(1) < ![]() <
S n, n =1,2, … . (2)
<
S n, n =1,2, … . (2)
1) Пусть интеграл (1) сходится. Тогда существует предел
![]() ,
,
так как
![]()
![]()
(в силу условия f(x) > 0 для ![]() , то из неравенства (2) следует, что
, то из неравенства (2) следует, что
S n < f(1) + ![]() ≤ f(1) + A = M = const,
≤ f(1) + A = M = const,
т.е. 0 < S n < M для n = 1, 2, … .Тем самым, последовательность {S n} ограничена, и при возрастании n сумма S n возрастает, так как f(n ) > 0 для n = 1, 2, … . Поэтому она имеет предел
![]() ,
,
Что означает сходимость ряда ![]() .
.
2) Пусть интеграл (1) расходится. Так как по условию
f(x) > 0 для ![]() , то
, то
![]() =
= ![]() .
.
Из неравенства
S n ≥ ![]() , n = 1, 2, … ,
, n = 1, 2, … ,
Следует, что
![]() ,
,
т.е. ряд ![]() расходится. ►
расходится. ►
Пример 1. Исследовать на сходимость ряд
![]() .
.
◄ Здесь ![]() . Известно, что несобственный интеграл
. Известно, что несобственный интеграл
![]()
сходится при p > 1 и расходится при p ≤ 1. Следовательно, данный ряд сходится при p > 1 и расходится
при p ≤ 1. В частности, при p = 1 получим гармонический ряд
![]() ►
►
Пример 2. Исследовать на сходимость ряд
![]() .
.
◄ В данном случае функция ![]() и
и
![]() =
=![]() =
=![]()
![]() =
=
=![]() (arctg b-arctg 1)=
(arctg b-arctg 1)= ![]() ,
,
т.е. интеграл
![]()
сходится, а значит, сходится и ряд. ►
Пример 3. Исследовать на сходимость ряд
![]()
◄ Так как общий член данного ряда имеет вид ![]() , то выбираем функцию
, то выбираем функцию ![]() .
.
Несобственный интеграл
![]() =
=![]() =
=![]() =
=
=![]() = +
= +![]()
расходится, следовательно, ряд тоже расходится. ►
Замечание. Нижний предел интегрирования в несобственном интеграле
![]()
можно взять произвольным, например, равным а, где а ≥ 1 – любое число.
Пример 4. Исследовать сходимость ряда
![]() ,
,
◄ Так как общий член ряда
![]()
то в качестве функции ![]() возьмем
возьмем
![]() , где x ≥ 4.
, где x ≥ 4.
Тогда
![]() =
=![]() =
=
=![]() =
=![]()
=![]()
![]() .
.
Так как несобственный интеграл
![]()
сходится, то сходится и исходный ряд. ►
В случае сходимости ряда ![]() метод, примененный при доказательстве интегрального признака сходимости, позволяет получить оценку погрешности, возникающей при замене суммы ряда частичной суммой.
метод, примененный при доказательстве интегрального признака сходимости, позволяет получить оценку погрешности, возникающей при замене суммы ряда частичной суммой.
Пусть функция f(x) удовлетворяет условиям теоремы 9, ряд
![]()
сходится и его сумма равна S. Можно показать, что в этом случае будет сходиться и несобственный интеграл
![]() .
.
Пользуясь неравенством
 ,
,
оценим остаток Rn заданного ряда, Имеем
 .
.
Итак,

Таким образом, погрешность, получаемая при замене суммы S сходящегося ряда ![]()
его n-й частичной суммой Sn , не превосходит интеграла 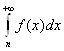 .
.
Пример 5. Установить сходимость ряда
![]()
и оценить погрешность при замене его суммы S5.
◄ Здесь
![]() =
=![]() =
=![]() = =
= =![]() =
=![]()
В силу интегрального признака ряд сходится. Обозначим сумму этого ряда через S и будем считать, что
S ≈ S5. Тогда
S ≈ S5 ==![]()
![]()
Оценим погрешность R5. Имеем
![]()
![]() ►
►
Замечание. Обозначение
![]()
понимается так
![]() =
=![]() =
=![]()
![]() =
=
=![]() .
.
Пример 6. Оценить n-й остаток сходящегося ряда
![]()
где p>1.
◄ Имеем
 =
=  =
= ![]() =
= ![]() . ►
. ►
Похожие работы
... получаться также абсолютно сходящиеся ряды, при этом сумма ряда не изменяется. Как указывалось в разделе 2, условно сходящиеся ряды таким свойством не обладают. Вопросы для самопроверки 1. Как определяется сумма числового ряда? 2. Какой ряд называется сходящимся (расходящимся)? 3. Может ли предел общего члена сходящегося числового ряда равняться 3? 4. Что можно сказать о сходимости чи
... , то отрицательны. Т.Лейбница: Если члены знакочередующегося ряда убывают по абсолютной величине U1>U2>U3… и предел его общего члена при n®¥ равен 0 (Lim n®¥ Un=0), то ряд сходится, а его сумма не превосходит первого члена: U1³S. Д: Рассмотрим последовательность частичных сумм четного числа членов при n=2m: S2m=(U1-U2)+(U3-U4)+…+(U2m-1-U2m). Эта последовательность ...
... такой же ряд, но члены имеют обратные знаки. . 9.3.7. а) Проверяем концы интервалов 1) Признак Лейбница выполняется, ряд сходится. При получится такой же ряд (т.к. x в четной степени). б) 9.3.8. а) Условие сходимости . Найдем дискриминант знаменателя: D=64-72<0. Условие принимает вид Интервал сходимости . На концах интервала Получаем один и ...
повторный по формуле: Сначала вычисляется внутренний интеграл, затем внешний. При вычислении внутреннего интеграла ‘х’ считается переменной, а ‘у’-постоянной. 3. Если область интегрирования не относится ни к 1 ни ко второму случаю, то разбиваем ее на части таким образом, чтобы каждая из частей относилась к одному из этих двух видов. Вычисление объемов тел с помощью двойного ...


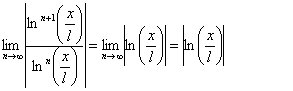

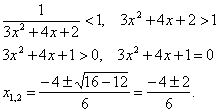
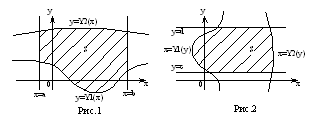
0 комментариев