Навигация
ВЫСШАЯ МАТЕМАТИКА
Числовые ряды
Содержание
Лекция. Числовые ряды
1. Определение числового ряда. Сходимость
2. Основные свойства числовых рядов
3. Ряды с положительными членами. Признаки сходимости
4. Знакочередующиеся ряды. Признак сходимости Лейбница
5. Знакопеременные ряды
Вопросы для самопроверки
Литература
Лекция. ЧИСЛОВЫЕ РЯДЫ
1. Определение числового ряда. Сходимость.
2. Основные свойства числовых рядов.
3. Ряды с положительными членами. Признаки сходимости.
4. Знакочередующиеся ряды. Признак сходимости Лейбница.
5. Знакопеременные ряды.
1. Определение числового ряда. Сходимость
В математических приложениях, а также при решении некоторых задач в экономике, статистике и других областях рассматриваются суммы с бесконечным числом слагаемых. Здесь мы дадим определение того, что понимается под такими суммами.
Пусть задана бесконечная числовая последовательность
![]() ,
, ![]() , …,
, …, ![]() , …
, …
Определение 1.1. Числовым рядом или просто рядом называется выражение (сумма) вида
![]() . (1.1)
. (1.1)
Числа ![]() называются членами ряда,
называются членами ряда, ![]() – общим или n–м членом ряда.
– общим или n–м членом ряда.
Чтобы задать ряд (1.1) достаточно задать функцию натурального аргумента ![]() вычисления
вычисления ![]() -го члена ряда по его номеру
-го члена ряда по его номеру ![]()
Пример 1.1. Пусть ![]() . Ряд
. Ряд
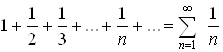 (1.2)
(1.2)
называется гармоническим рядом.
Пример 1.2. Пусть ![]() ,
, ![]() Ряд
Ряд
![]() (1.3)
(1.3)
называется обобщенным гармоническим рядом. В частном случае при ![]() получается гармонический ряд.
получается гармонический ряд.
Пример 1.3. Пусть ![]() =
=![]() . Ряд
. Ряд
![]() (1.4)
(1.4)
называется рядом геометрической прогрессии.
Из членов ряда (1.1) образуем числовую последовательность частичных сумм ![]() где
где ![]() – сумма
– сумма ![]() первых членов ряда, которая называется n-й частичной суммой, т. е.
первых членов ряда, которая называется n-й частичной суммой, т. е.
![]() ,
,
![]() ,
,
![]() ,
,
…………………………….
![]() , (1.5)
, (1.5)
…………………………….
Числовая последовательность ![]() при неограниченном возрастании номера
при неограниченном возрастании номера ![]() может:
может:
1) иметь конечный предел;
2) не иметь конечного предела (предел не существует или равен бесконечности).
Определение 1.2. Ряд (1.1) называется сходящимся, если последовательность его частичных сумм (1.5) имеет конечный предел, т. е. ![]()
В этом случае число ![]() называется суммой ряда (1.1) и пишется
называется суммой ряда (1.1) и пишется
![]() .
.
Определение 1.3. Ряд (1.1) называется расходящимся, если последовательность его частичных сумм не имеет конечного предела.
Расходящемуся ряду не приписывают никакой суммы.
Таким образом, задача нахождения суммы сходящегося ряда (1.1) равносильна вычислению предела последовательности его частичных сумм.
Рассмотрим несколько примеров.
Пример 1.4. Доказать, что ряд

сходится, и найти его сумму.
Найдем n-ю частичную сумму данного ряда ![]() .
.
Общий член 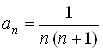 ряда представим в виде
ряда представим в виде 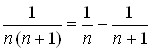 .
.
Тогда 
Отсюда имеем: ![]() . Следовательно, данный ряд сходится и его сумма равна 1:
. Следовательно, данный ряд сходится и его сумма равна 1:
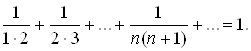
Пример 1.5. Исследовать на сходимость ряд
![]() (1.6)
(1.6)
Для этого ряда ![]()
![]() . Следовательно, данный ряд расходится.
. Следовательно, данный ряд расходится.
Замечание. При ![]() ряд (1.6) представляет собой сумму бесконечного числа нулей и является, очевидно, сходящимся.
ряд (1.6) представляет собой сумму бесконечного числа нулей и является, очевидно, сходящимся.
Пример 1.6. Исследовать на сходимость ряд
![]() (1.7)
(1.7)
Для этого ряда 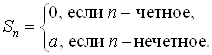
В этом случае предел последовательности частичных сумм ![]() не существует, и ряд расходится.
не существует, и ряд расходится.
Пример 1.7. Исследовать на сходимость ряд геометрической прогрессии (1.4):
![]()
Нетрудно показать, что n-я частичная сумма ряда геометрической прогрессии при ![]() задается формулой
задается формулой
 .
.
Рассмотрим случаи:
1) ![]() Тогда
Тогда ![]() и
и 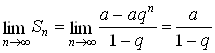 .
.
Следовательно, ряд сходится и его сумма равна ![]()
2) ![]() .
.![]()
Тогда ![]() и
и 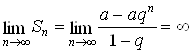 .
.
Следовательно, ряд расходится.
3) ![]() или
или ![]() Тогда исходный ряд имеет вид (1.6) или (1.7) соответственно, которые расходятся. Окончательно имеем
Тогда исходный ряд имеет вид (1.6) или (1.7) соответственно, которые расходятся. Окончательно имеем
 (1.8)
(1.8)
Пример 1.8. Найти сумму ряда
![]()
Очевидно, что данный ряд является рядом геометрической прогрессии. В нашем случае ![]() . Тогда из формулы (1.8) следует
. Тогда из формулы (1.8) следует
![]() .
.
Исследование на сходимость гармонического ряда (1.2) и обобщенного гармонического ряда (1.3) будет проведено в следующем разделе.
Похожие работы
... Неопределенный интеграл от функции для всех может быть получен почленным интегрированием ряда (1.2), т. е. для всех . Следует отметить, что при почленном дифференцировании и интегрировании степенного ряда его радиус сходимости R не меняется, однако его сходимость на концах интервала может измениться. Приведенные свойства справедливы также и для степенных рядов (1.1). Пример 2.1. ...
... до бесконечности вместе с n. 1.2 Истоки проблемы Различные факты из области математического анализа, как, например, расходимость, произведения двух сходящихся рядов, естественно выдвинули вышеупомянутый вопрос: “О возможности суммирования расходящихся рядов, в некоем новом смысле”. Нужно сказать, что до создания Коши строгой теории пределов (и связанной с нею теории рядов) расходящиеся ...
... . Упражнение. Доказать, что, если на всей оси функция y(х) дифференцируема, а j(х) – дважды дифференцируема, то функция (13.11) действительно удовлетворяет уравнению (13.9) и начальным условиям (13.10). Глава 3. Операционное исчисление § 14. Преобразование Лапласа Понятие оригинала. Кусочно-непрерывная функция называется оригиналом, если выполняются следующие условия: 1) для всех ...
... действительные числа любого знака, называется знакопеременным. Знакопеременными будут, например, ряды , (плюс, два минуса, плюс, два минуса и т.д.). Наряду со знакопеременным рядом рассмотрим ряд, составленный из абсолютных величин его членов, т.е. , и докажем следующую теорему. Теорема 5. Если сходится ряд , то сходится и ряд ◄ Из двойного неравенства ...



0 комментариев