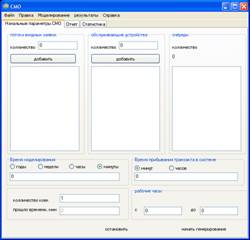
Навигация
Собственно, обслуживание
1. собственно, обслуживание
2. ожидание обслуживания заявки
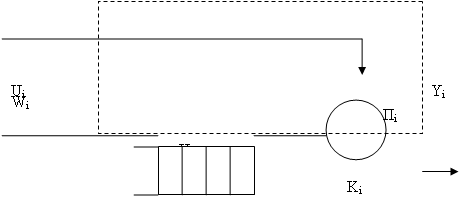
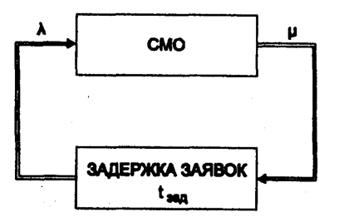
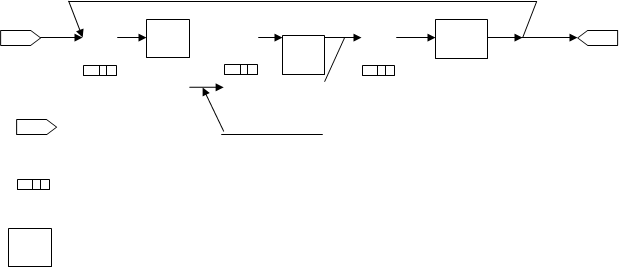
K – канал, Н – накопитель, П – прибор обслуживания
В i-ом приборе обслуживания имеем:
· wi – поток заявок т.е. интервалы времени между моментами появления заявок (вызывающие моменты) на входе канала Ki.
· ui – поток обслуживания – интервалы времени между началом и окончанием обслуживания заявок.
Заявки, обслуженные каналом, и заявки, покинувшие i-ый прибор не обслуженными, образуют выходной поток Yi, т.е. интервалы времени между моментами выхода заявок.
Процесс функционирования прибора Пi можно представить как процесс изменения состояний его элементов во времени. Переход в новое состояние для прибора означает изменение количества заявок, которые в нем находятся.
![]()
![]()

где Z – заявка, L – емкость накопителя
В практике моделирование элементарные Q-схемы обычно объединяются. При этом, если каналы различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание, а если последовательно – то многофазное. Следовательно, для задания Q-схемы необходимо использовать некоторый оператор - R-оператор сопряжения, отражающий взаимосвязь элементов структуры между собой.
Различают разомкнутые и замкнутые Q-схемы. В разомкнутых схемах выходной поток не может попасть на вход, а в замкнутых схемах количество заявок постоянно.
Собственными внутренними параметрами Q-схемы будут являться:
· Количество фаз
· Количество каналов в каждой фазе
· Количество накопителей в каждой фазе
· Емкость i-ого накопителя
В зависимости от емкости накопителя в теории массового обслуживания принято:
· Емкость 0 – система с потерями.
· Емкость ® ¥ - система с ожиданием
· Емкость конечна – система смешанного типа
Для задания функционирования Q-схемы также необходимо описать алгоритм её функционирования, который определяет набор правил поведения заявок в различных ситуациях.
Неоднородность заявок, отражающая реальный процесс учитывается введением классов приоритетов. Следовательно, Q-схема, описывающая процесс функционирования системы массового обслуживания любой сложности, однозначно задается:
Q = (W, U, R, H, Z, A)
1. W - подмножеством входных потоков
2. U - подмножеством потоков обслуживания
3. H - подмножеством собственных параметров
4. R - оператором сопряжения элементов структуры
5. Z - множеством состояний элементов системы
6. A - оператором алгоритмов обслуживания заявок
Для получения соотношений, связывающих характеристики описания функционирования Q-схемы вводятся некоторые допущения относительно входных потоков, функций распределения параметров, длительности обслуживания запросов, дисциплин обслуживания.
Для математического описания функционирования устройств, развивающегося в форме случайного процесса, может быть использован математический аппарат, который носит название Марковского случайного процесса.
Случайный процесс, протекающий в некоторой системе называется Марковским случайным процессом, если он обладает следующим свойством: для каждого момента времени t0 вероятность любого состояния системы в будущем (при t > t0) зависит только от состояния системы в настоящем и не зависит от того, когда и каким образом система пришла в это состояние.
В марковском случайном процессе будущее развитие зависит только от настоящего состояния и не зависит от предыстории. Для марковских случайных процессов определяется вероятности нахождения системы в том или ином состоянии используя уравнения Колмогорова:
![]() ,
,
где p(t) – вероятность попадания в какое-либо состояние
l - множество определенных коэффициентов
Для стационарного потока:
![]()
![]() - базисная модель
- базисная модель
![]() - интерфейсная модель
- интерфейсная модель
Математическая модель некоторой сложной системы строится как совокупность базисной модели и интерфейсной модели, что позволяет использовать одни и те же базисные модели для разных задач проектирования, осуществляя настройку на соответствующую конкретную задачу, посредством изменения только параметров интерфейсной модели.
Математическая модель сложной Q-схемы должна обеспечивать вычисление времени реакции на запрос и производительность системы.
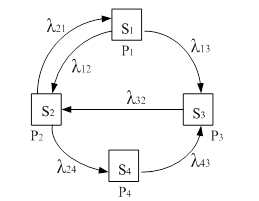
Методика вывода уравнений Колмогорова
![]()
![]() -интенсивность перехода
-интенсивность перехода
![]()
1. Найдем вероятность того, что в момент времени t система
находится в состоянии S1. Придадим t малое приращение Dt и
определим, что система в момент времени t+Dt находится в состоянии S1.
![]()
![]()
![]()
2. Найдем вероятность того, что система находится в состоянии S2:
![]()
![]()
![]()
3. Найдем вероятность того, что система находится в состоянии S3:
![]()
4. Найдем вероятность того, что система находится в состоянии S4:
![]()
В результате получаем систему уравнений Колмогорова:
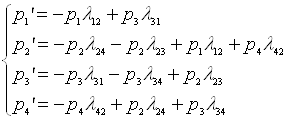
Интегрирование данной системы даст искомые вероятности состояний, как функций времени. Начальные условия берутся в зависимости от того, какого было начальное состояние системы. Если при t=0 система находится в состоянии S1, то начальные условия будут p1=1, p2= p3= p4=0. Кроме этого, к системе добавляются условия нормировки:
![]()
Все уравнения строятся по определенному правилу:
1. В левой части каждого уравнения стоит производная вероятности состояния, а в правой части содержится столько членов, сколько стрелок связано с этим состоянием.
2. Если стрелка направлена «из» состояния, соответствующий член имеет знак “-“, если «в» состояние, то знак “+”.
3. Каждый член равен произведению плотности вероятности перехода (интенсивность), соответствующий данной стрелке, и вероятности того состояния, из которого выходит стрелка.
Пример.
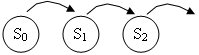
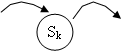
Рассмотрим многоканальную СМО с отказами. Состояние системы характеризуется по числу занятых каналов, т.е. по числу заявок.
S0 – все каналы свободны
S1 – занят один канал, остальные свободны
Sk – занято k каналов, остальные свободны
Sn – заняты все n каналов.
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||
 |  | ||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||
Разметим граф, т.е. проставим у стрелок интенсивности соответствующих потоков событий. Пусть система находится в состоянии S1. Как только закончится обслуживание заявки, занимающей этот канал, система переходит в состояние S0, интенсивность перехода m. Если занято 2 канала, а не один, то интенсивность перехода составит 2m.

Предельные вероятности состояний p0и pn характеризую установившийся режим работы системы массового обслуживания при t® ¥.
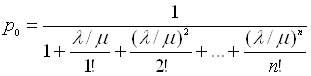

![]() - среднее число заявок, приходящих в систему за среднее время обслуживания одной заявки.
- среднее число заявок, приходящих в систему за среднее время обслуживания одной заявки.

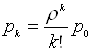
Зная все вероятности состояний p0, … , pn , можно найти характеристики СМО:
· вероятность отказа – вероятность того, что все n каналов заняты
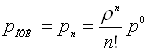
· относительная пропускная способность – вероятность того, что заявка будет принята к обслуживанию
![]()
· среднее число заявок, обслуженных в единицу времени
![]()
Полученные соотношения могут рассматриваться как базисная модель оценки характеристик производительности системы. Входящий в эту модель параметр l = 1 / tОБРАБОТКИ, является усредненной характеристикой пользователя. Параметр m является функцией технических характеристик компьютера и решаемых задач.
Эта связь может быть установлена с помощью соотношений, называемых интерфейсной моделью. Если время ввода/вывода информации по каждой задачи мало по сравнению со временем решения задачи, то логично принять, что время решения равно 1 / m и равно отношению среднего числа операций, выполненных процессором при решении одной задачи к среднему быстродействию процессора.
На практике далеко не все случайные процессы являются Марковскими или близкими к ним. В СМО поток заявок не всегда Пуассоновский, ещё реже наблюдается показательное или близкое к нему распределение времени обслуживания.
Для произвольных потоков сообщений, переводящих систему из одного состояния в другое, аналитическое решение получено только для отдельных частных случаев. Когда построение аналитической модели по той или иной причине трудно осуществимо, применяется другой метод моделирования – метод статистических испытаний (Монте-Карло). Широкое распространение метода связано с возможностью его реализации на компьютере.
Идея метода: вместо того, чтобы описывать случайное явление с помощью аналитической зависимости производится «розыгрыш», т.е. происходит моделирование случайного явления с помощью некоторой процедуры, дающей случайный результат. Произведя такой розыгрыш n раз, получаем статистический материал, т.е. множество реализаций случайного явления, которое потом можно обработать обычными методами математической статистики. Метод Монте-Карло предложил Фон-Нейман в 1948 году, как метод численного решения некоторых математических задач.
Суть метода:
1. Вводим в некотором единичном квадрате любую поверхность S.
2. Любым получаем 2 числа xi, yi, подчиняющиеся равномерному закону распределения случайной величины на интервале [0, 1].
3. Полагаем, что одно число определяет координату x, второе – координату y
4. Анализируем принадлежность точки (x, y) фигуре. Если принадлежит, то увеличиваем значение счетчика на 1.
5. Повторяем n раз процедуру генерации 2х случайных чисел с заданным законом распределения и проверку принадлежности точки поверхности S.
6. Определяем площадь фигуры как количество попавших точек, к количеству сгенерированных.
Фон-Нейман доказал, что погрешность  .
.
Преимущества метода статистических испытаний в его универсальности, обуславливающей возможность всестороннего статистического исследования объекта, однако, для реализации этой возможности нужны довольно полные статистические сведения о параметрах элементов.
К недостаткам относится большой объем требуемых вычислений, равный количеству обращений к модели. Поэтому вопрос выбора величины n имеет важнейшее значение. Уменьшая n – повышаем экономичность расчетов, но одновременно ухудшаем их точность.
Способы получения последовательностей случайных чисел
На практике используются 3 основных способа генерации случайных чисел:
1. аппаратный (физический)
2. табличный (файловый)
3. алгоритмический (программный)
Аппаратный способ.
Случайные числа вырабатываются специальной электронной приставкой (генератором случайных чисел). Реализация этого способа не требует дополнительных вычислительных операций по выбору случайных чисел. Необходимо только оперативное обращение к ВУ.
В качестве физического эффекта, лежащего в основе генератора, чаще всего используют шуму в электронных приборах.
Простейшие алгоритмы генерации последовательности псевдослучайных чисел
Одним из первых способов получения является выделение значения дробной части у многочлена первой степени:
![]()
Если n пробегает значения натурального ряда числе, то поведение yn выглядит весьма хаотично.
К. Якоби доказал, что при рациональном коэффициенте a множество y конечно, а при иррациональном – бесконечно и всюду плотно в интервале [0, 1].
Критерий равномерности распределения любой функции: свойство эргамичности – среднее по реализациям псевдослучайное число равно среднему по всему их множеству с вероятностью 1.
1. 1946 год, Фон Нейман.
Каждое последующее случайное число образуется возведением в квадрат предыдущего и отбрасывание цифр с обоих концов. Способ оказался ненадежным.
2. Лемер.
![]() . Для подборов коэффициентов k, c, m были потрачены десятки лет. Подбор почти иррациональных чисел ничего не дает.
. Для подборов коэффициентов k, c, m были потрачены десятки лет. Подбор почти иррациональных чисел ничего не дает.
3. Разумнее ввести вычисления с целыми числами.
при c = 0 и m = 2n наибольший период достигается при k=3+8i или k=5+8i и при нечетном начальном числе.
Для имитации равномерного распределения на [a, b] используется обратное преобразование функции плотности вероятности.

где R – равномерно распределенное псевдослучайное число на [0, 1].
В основе построения программы генерации случайной числа с законом распределения, отличным от равномерного, лежит метод преобразования последовательности случайных чисел с равномерным законом распределения в последовательность случайных чисел с заданным законом распределения.
Метод основан на том, что случайная величина x принимает значения, равные корню уравнения
![]()
, имеет плотность распределения f(x). R – случайная величина, равномерно распределенная на [0, 1].
Значение случайной величины, распределенной по показательному закону может быть вычислено из данного уравнения следующим образом:
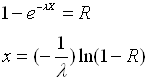
Распределение Пуассона относится к числу дискретных (переменная может принимать лишь целочисленные значения, включая 0, с математическим ожиданием и дисперсией l > 0). Для генерации Пуассоновских переменных можно использовать метод точек, в основе которого лежит генерируемое случайное значение Ri , равномерно распределенное на [0, 1], до тех пор, пока не станет справедливым
![]()
При получении случайной величины, функция распределения которой не позволяет найти решение уравнения
![]()
в явной форме, можно произвести кусочно-линейную аппроксимацию, а затем вычислить приближенное значение корня. Кроме того, при получении случайной величины часто используют те или иные свойства распределений.
Воспользуемся этим методом, чтобы сгенерировать случайную величину с законом распределения Эрланга. Распределение Эрланга характеризуется параметрами l и k.
При вычислении случайно величины воспользуемся тем, что поток Эрланга может быть получен путем прорешивания потока Пуассона k раз. Поэтому, достаточно получить k значений случайной величины распределенной по показательному закону и усреднить их.
![]()
Нормальное распределение случайной величины может быть получено как сумма большого числа случайных величин, распределенных по одному и тому же закону распределения с одними и теми же параметрами.
Случайная величина X имеющая нормальное распределение с математическим ожиданием MX и среднеквадратичным отклонением sX может быть получена по следующей формуле:

Для сокращения вычислений на практике принимаю N=12, что дает вполне относительно хорошее приближение к нормальному распределению.
Немарковские случайные процессы, сводящиеся к марковским
Реальные процессы часто обладают последствием и поэтому не являются марковскими. Иногда при исследовании таких процессов удается воспользоваться методами, разработанными для марковских процессов. Наиболее распространены два способа:
Похожие работы
... как точки на временной оси. Для достижения основной цели моделирования достаточно наблюдать систему в моменты реализации основных событий. Рассмотрим пример одноканальной системы массового обслуживания. Целью имитационного моделирования подобной системы является определение оценок ее основных характеристик, таких, как среднее время пребывания заявки в очереди, средняя длина очереди и доля ...
... каналов обслуживан6ия, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами. Задача теории массового обслуживания - установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных ...
... 6. Петухов О.А. , Морозов А.В. , Петухова Е.О. Моделирование системное, имитационное, аналитическое. Учебное пособие – Санкт-Петербург 2008 7. Норенков И.П., Федорук Е.В.Имитационное моделирование систем массового обслуживания. Методические указания – Москва 1999 8. Кутузов О.И., Татарникова Т.М., Петров К.О. Распределенные информационные системы управления. Учебное пособие – Санкт-Петербург ...
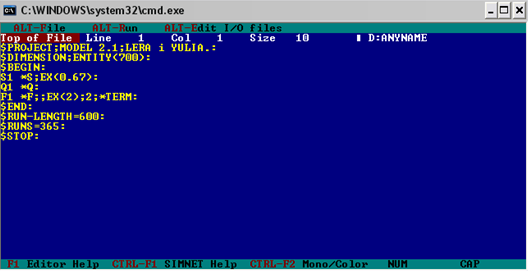
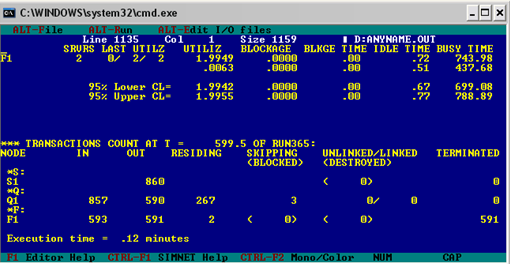
... *0,1*25 – 1*,09 = 2148,2 ден.ед. Таким образом, максимальная прибыль достигается при установлении трех телефонных линий. Программа имитационного моделирования для оптимального режима работы примет вид: имитационный моделирование массовый обслуживание Результаты расчетов функциональных характеристик СМО: Характеристика Значение l 1/0,67 = 1,5 зв./мин. m 60/2=30 зв./мин. ...
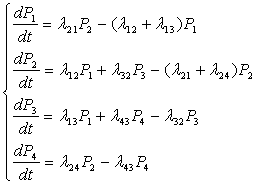

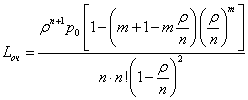
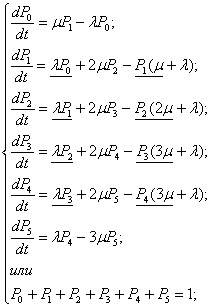





0 комментариев