Навигация
В качестве c следует выбирать нечетное число, такое, что
3. В качестве c следует выбирать нечетное число, такое, что
![]() .
.
Более подробные рекомендации по выбору параметров можно найти у Д. Кнута [5].
При использовании конгруэнтного ГСЧ следует помнить, что наименее значимые двоичные цифры xk будут «не очень случайными». Поэтому, если, например, вы хотите использовать число xk для случайного выбора одной из 16 возможных ветвей, берите наиболее значимые разряды xk, а не наименее значимые. Наконец, для большей надежности полезно предварительно испытать случайные числа на какой-либо задаче с известным ответом, схожей с реальным приложением.
5. Генерирование чисел с произвольным распределением
Достаточно часто возникает необходимость сгенерировать последовательность случайных чисел yi, равномерно распределенных на данном конечном интервале [a, b], с помощью ГСЧ, выдающего числа xi на интервале [0, m]. Приведение диапазона ГСЧ к нужному интервалу в этом случае осуществляется простым линейным преобразованием:
![]() .
.
Распределение чисел после такого преобразования остается равномерным.
Более сложным случаем является генерирование случайных точек из некоторого множества в n‑мерном пространстве Rn, например, точек из некоторой области на плоскости. Рассмотрим формирование случайных точек для нескольких простых областей: прямоугольника, окружности и круга.

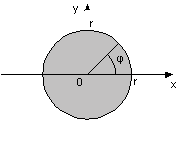
а) б) в)
Рис. 2. Области, из которых выбираются точки
Для получения равномерно распределенных случайных чисел из прямоугольника, стороны которого параллельны осям координат (см. рис.2, а), достаточно извлекать из ГСЧ последовательно пары чисел, приводить их к нужным интервалам и использовать как координаты точки:
![]()
![]() ,
,
где uj – равномерно распределенное случайное число из отрезка [0, m].
Окружность можно представить одномерным множеством точек с угловой координатой φ, принимающей значения на интервале (0, 2π). Таким образом, декартовы координаты очередной точки можно вычислить следующим образом:
![]()
![]()
![]() .
.
где uj – равномерно распределенное случайное число из интервала (0, m); r – радиус окружности.
В случае круга первое, что приходит в голову – воспользоваться полярной системой координат (ρ, φ), в которой данное множество фактически представляет собой прямоугольник (а для него способ генерации чисел известен). Однако при переходе от полярных координат к декартовым нарушается распределение случайных чисел: оно становится неравномерным; плотность распределения в центре круга выше, чем по краям.
Существует несколько способов получения равномерного распределения по кругу. Рассмотрим один из них. Будем генерировать случайные пары (x, y) и для каждой из них ставить внутри круга соответствующую точку, заполняя таким образом эту область. Исходя из представлений о равномерном распределении можно предположить, что при достаточно большой длине сгенерированной последовательности на единицу площади круга будет приходиться примерно одно и то же количество точек вне зависимости от их расположения (другими словами, при равномерном распределении плотность точек по кругу будет одинакова).
Воспользуемся полярной системой координат для генерирования точек. При этом будем выбирать угол φ равномерно распределенным на интервале (0; 2π), а распределение ρ построим следующим образом:
![]() ,
,
где x – равномерно распределенная на отрезке [0; 1] случайная величина. Можно показать, что при таком способе формирования координат случайные точки будут равномерно распределены по всей площади круга.
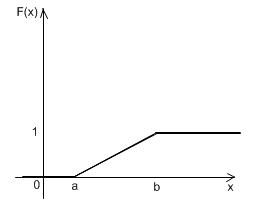
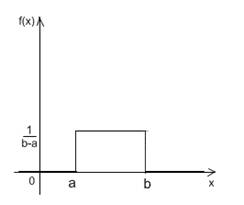
Помимо выбора из произвольного множества, часто требуется формировать числа с распределением, отличным от равномерного. Распределение обычно задается функцией плотности распределения f(x) либо функцией распределения F(x). Функция распределения в произвольной точке x показывает вероятность того, что случайная величина X окажется меньше данного значения x:
F(x)=P (X<x).
Функция плотности распределения представляет собой производную F(x):
![]() .
.
Функция F(x) для любой случайной величины является неубывающей на всем интервале (–∞; +∞), стремится к 0 при x→ –∞ и к 1 при x→ +∞. Для получения случайных чисел с заданным распределением F(x) необходимо найти функцию, обратную к F(x), т.е. такую функцию G, что для всех y=F(x) выполняется G(y)=x. Это можно пояснить следующим образом. Предположим, что мы многократно выбираем число y, равномерно распределенное на интервале [0; 1]; каждому y мы ставим в соответствие некоторое x=G(y). Выбору 50000 игреков соответствует выбор 50000 иксов. Таким образом, доля выбранных y, лежащих между двумя фиксированными значениями, скажем y1 и y2, в точности равна доле x, лежащих в интервале [x1; x2]. Но вероятность первого из названных событий равна | y2 – y1 |, если y распределено равномерно; следовательно, верна цепочка равенств:
доля чисел в интервале [x1; x2] = доля чисел в интервале [y1; y2] = y2 – y1 = F(x2) – F(x1) = 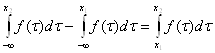 ,
,
которая и показывает, что в случае равномерного распределения игреков x имеет распределение с плотностью f(τ). Сложной проблемой в этом подходе является достаточно быстрое и точное формирование обратной функции распределения G(y).
Рассмотрим в качестве примера получение случайного числа с экспоненциальным распределением. Это распределение характеризуется одним параметром λ>0 и имеет следующие функции распределения и плотности распределения:
![]() , x≥0;
, x≥0;
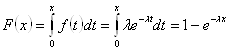 .
.
Для этого распределения легко получить F–1 (y), т.е. разрешить уравнение F(x)=y. Решение имеет вид
![]() .
.
Для получения x с искомым распределением нужно сгенерировать y, равномерно распределенное на (0,1), и применить эту формулу. Если говорить о практической стороне дела, то существуют более эффективные способы, в которых не используется медленная операция вычисления логарифма для каждого случайного числа. Данный способ продемонстрирован лишь как пример более общего подхода с использованием обратной функции распределения.
Похожие работы
... на выходах генератора формируются два числа (на выходе счётчика 2 и выходе сумматора 10). Первое из них соответствует нечёткому значению интервала времени, необходимого для достижения поставленной цели, а второе - нечёткому значению результата настройки. В отличие от известных предложенный метод (алгоритм) позволил создать простой по своей структуре генератор случайных чисел, у которого наработка
... η с функцией распределения F(y) из случайной величины ζ, равномерно-распределенной в интервале [0,1], используются различные методы. К основным методам моделирования случайных чисел с заданным законом распределения относятся: - метод обратной функции - метод отбора или исключения - метод композиции. 2. Метод обратной функции Если ζ- равномерно-распределенная на интервале ...
... величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.2.2. Начало алгоритмизации. Для получения двух последовательностей из 50 случайных чисел с показательным и нормальным законами распределения необходимо организовать цикл, который будет выполнятся 50 раз. Внутри цикла будем пользоваться функцией из Турбо Паскаля ...
... нельзя в полной мере назвать случайными, поскольку между ними имеется зависимость, а также наличие периодов в последовательности псевдослучайных чисел. К алгоритмическим методам получения ГСЧ относиться метод серединных квадратов, предложенный в 1946 г. Дж. фон Нейманом. Метод серединных квадратов Имеется некоторое четырехзначное число R0. Это число возводится в квадрат и заносится в R1. Далее ...
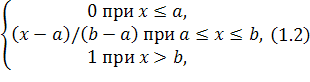
0 комментариев