Навигация
Методы решения задач в частных производных
1.2 Методы решения задач в частных производных
Среди дифференциальных уравнений в частных производных можно выделить уравнения, описывающие стационарные распределения в заданной области некоторой физической величины, и уравнения, описывающие изменение во времени распределенной в заданной области физической величины. Признаком, разделяющим уравнения на эти два подмножества, является присутствие в уравнении частной производной по времени. Принципиальное различие пространственной и временной независимых переменных состоит в том, что в отличие от однонаправленного изменения реального времени ортогональные пространственные переменные могут изменяться независимо друг от друга в обоих направлениях.
Ядром наиболее часто встречающихся дифференциальных уравнений в частных производных служит уравнение Лапласа
![]() ,
,
где ![]() (набла в квадрате) - оператор Лапласа, который в двумерной декартовой системе координат имеет вид
(набла в квадрате) - оператор Лапласа, который в двумерной декартовой системе координат имеет вид
 .
.
Это уравнение описывает стационарное поле некоторой физической величины и относится к уравнениям эллиптического, гиперболического или параболического типа в зависимости от значения определителя дифференциальной формы второй степени
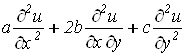 , для которой соответственно
, для которой соответственно 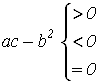 ,
,
где ![]() - в общем случае функции координат и потенциала u.
- в общем случае функции координат и потенциала u.
К нестационарным уравнениям параболического и гиперболического типов относятся соответственно уравнение теплопроводности с параметрами-функциями s и S
![]()
и уравнения волновое и бигармоническое с параметром С
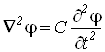 и
и 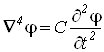
Названные уравнения представлены в канонической форме, которая включает безразмерные относительные переменные, обычно приводимые к диапазонам изменения [0,1] и [-1,1]. Размерности слагаемых согласуются посредством параметров уравнения.
Основным методом решения дифференциальных уравнений в частных производных является аппроксимация уравнения системой алгебраических уравнений или системой дифференциальных уравнений. Эти два вида аппроксимаций в литературе получили название метод сеток и метод прямых.
Метод сеток реализуется в том случае, когда частные производные, входящие в уравнение, заменяются в каждой точке заданной области конечно-разностными выражениями, полученными из значений искомого решения в окружающих точках. Количество уравнений в системе связано с шагом дискретизации временной и пространственных переменных и формой границы области решения. Число точек, попавших внутрь области решения, определяет число неизвестных и уравнений.
Метод прямых относится к случаю, когда одна из независимых переменных является временем (случай нестационарных задач) или когда одну из пространственных переменных (случай стационарных задач) пропорционально связывают со временем. Частные производные от независимых переменных, не связанных с временем, аппроксимируют конечными разностями. В результате, оставшиеся дискретными независимые переменные сочетанием своих значений определяют общее число дифференциальных уравнений, которые в общем случае являются краевыми.
Аппроксимирующие дифференциальные уравнения с краевыми условиями невозможно интегрировать как систему уравнений Коши. Линейная система краевых задач многократно решается с частными начальными условиями и по результатам решений краевые условия пересчитываются в начальные. Нелинейной системе для приближенного вычисления начальных условий потребуются итерационные процедуры, рассмотренные выше.
Математические модели, сформированные по методам сеток и прямых, могут быть решены методом математического моделирования с применением аналоговых или псевдо аналоговых операционных блоков, а также методом аналогий.
Метод аналогий (аналоговое моделирование) заключается в том, что для каждого уравнения математической модели подбирается физический объект, переменные состояния которого связаны таким же уравнением. В подавляющем большинстве случаев в качестве аналоговых объектов используются схемы с электрическими и электронными компонентами. Особенно простыми аналогами уравнений математических моделей являются уравнения электрических схем, полученные на основании законов Ома и Кирхгофа.
Итак, все рассмотренные методы используют конечно-разностную аппроксимацию, к рассмотрению которой мы переходим.
Похожие работы
... равенства и неравенства. При полном равенстве в распределении доходов "кривая Лоренца" представляла бы собой прямую и, наоборот, кривизна усиливается по мере роста неравенства. В соответствии с современной экономической теорией нежелательно как абсолютное равенство в распределении доходов, так и резкий разрыв в уровне жизни различных групп населения. Абсолютное равенство в доходах не стимулирует ...
... . Сложность совместной работы и обмена имеющейся информацией обусловлена ее высокой стоимостью, секретностью, проблемами достоверности и совместимости данных. 2.3 Информационные технологии управления муниципальной недвижимостью Эффективное управление объектами недвижимости должно обеспечить: - полный учет объектов муниципальной собственности; - эффективный контроль за использованием ...
... интервал времени. В этом случае поведение АСОД может быть представлено только в дискретных точках (группа динамических моделей с дискретным временем). 6 Описание программы автоматизации учета исполнения бюджета Краснодарского края 6.1 Средства разработки 6.1.1 Компилятор BORLAND PASCAL 7.0 Программа написана на языке Turbo Pascal версии 7.0. Турбо Паскаль появился на рынке программных ...
0 комментариев