Сортування включенням із зменшуваними відстанями – алгоритм Шелла (1959)

2.1 Сортування включенням із зменшуваними відстанями – алгоритм Шелла (1959)

Шелл вдосконалив пряме включення. Він запропонував проводити послідовне впорядкування підмасивів з елементів, які знаходяться на великих відстанях. При цьому на кожному наступному етапі відстані між елементами в групах мають зменшуватися.

Для ілюстрації алгоритму розглянемо його покрокове описання. Не обмежуючи загальності, в якості прикладу спочатку зупинимося на масиві з кількістю елементів, що є степенем двійки, тобто :

1) на першому етапі окремо групуються і сортуються елементи, розміщені на відстані N/2 . Це є впорядкування N/2 підмасиві по 2 елементи, яке називатимемо N/2-сортування .

2) на другому етапі виконується впорядку вання N/4 підмасивів по 4 елементи на відстані N/4 - N/4-сортування і т.д.

На останньому етапі виконується одинарне сортування (впорядкування на відстані 1). Наприклад :

44 55 12 42 94 18 06 67

етап I-сортування

44 18 06 42 94 55 12 67

етап II-сортування

06 18 12 42 44 55 94 67

етап III-сортування

06 12 18 42 44 55 67 94

Виникає питання, чи використання багатьох процесів сортування із залученням всіх елементів не збільшить кількість операцій, тобто складність алгоритму? Але на кожному проході або впорядковується відносно мало елементів (початкові етапи), або елементи вже досить добре впорядковані і вимагається відносно мало перестановок (кінцеві етапи). Кожне i-те сортування об’єднує дві групи, вже впорядковані 2i-тим сортуванням. Очевидно, що відстань між елементами груп можна зменшувати по-різному, головне, щоб остання була одиничною. Останній прохід в найгіршому випадку і виконує основну роботу. Варто зауважити, що такий довільний підхід при зменшенні відстаней не погіршує результату і у випадку кількості елементів N, що не є степенем двійки.

Нехай виконується t етапів. Відстані між елементами в окремих групах на кожному етапі позначимо : h₁ , h₂ , ..., h _t , де h _t=1, h _i+1<h _i , i=1, 2, ..., t-1. Таким чином розглядаються h-ті сортування. Кожне h-те сортування можна реалізувати будь-яким із прямих методів. Зокрема, вибір включення оправданий кращою в порівнянні з іншими алгоритмами ефективністю по перестановках ключів. Однак, чи варто для спрощення умови припинення пошуку місця включення чергового елемента користуватися методом бар’єрів? Оскільки кожне h-те сортування потребує свого власного бар’єра, то прийдеться розширити масив не на одну компоненту a₀ , а на h₁ компонент. На першому етапі - це практично половина всіх елементів. У випадку "довгих" масивів прийдеться порушити правило сортування "на своєму місці". Тому не варто заради економії однієї логічної операції на кожному етапі впорядкування жертвувати такими об’ємами пам’яті.

Кількість етапів сортування t як і відстані на кожному з них можна вибирати довільно. Зокрема, це може бути кількість цілочисельних поділів числа N на 2, тобто t=[log(N)]. В якості прикладу пропонується процедура сортування методом Шелла для масиву із 16 елементів :

 

Procedure Shell_Sort;

Const t=4;

Var

m, i, j, k : integer;

h : array [1..t] of integer;

x : basetype;

Begin

h[1]:=8; h[2]:=4; h[3]:=2; h[4]:=1;

for m:=1 to t do

begin

k:=h[m];

for i:=k+1 to N do

begin

x:=a[i]; j:=i-k;

while (x<a[j]) and (j>0) do

begin

a[j+k]:=a[j]; j:=j-k

end;

a[j+k]:=x

end

end

End;

 

Аналіз алгоритму Шелла. Поки що не має чітко обгрунтованих виборів відстаней, які давали б найкращу ефективність. Самим цікавим є те, що ці відстані не повинні бути множниками один одного, а тим більше степенями деяких чисел. Це дозволяє уникнути явища, коли на певному етапі взаємодіють дві групи, які до цього ніде ще не перетиналися. Взагалі, бажано, щоб взаємодія окремих ланцюгів відбувалася якомога частіше. Вірною є наступна теорема :

Теорема. Якщо k-відсортовану послідовність i-відсортувати, то вона при цьому залишиться k-відсортованою.

Кнут рекомендує використовувати такі послідовності відстаней, записані в зворотньому порядку :

1, 4, 13, 40, 121, ... , де h_i-1=3h_i+1 , h_t=1 , t=[log ₃ N]-1 , або

1, 3, 7, 15, 31, ... , де h_i-1=2h_i+1 , h_t=1 , t=[log ₂ N]-1.

З обчислювальної практики відомо, що загалом метод Шелла має ефективність порядку O(N^1,2).

2.2 Сортування обміном на великих відстанях – алгоритм Quick Sort

Основна причина повільної роботи алгоритму прямого обміну полягає в тому, що всі порівняння і перестановки елементів в послідовності a ₁ , a ₂ , ..., a _N відбуваються для пар із сусідніх елементів. При такому способі потрібно відносно більше часу, щоб поставити деякий ключ, який знаходиться не на своєму місці, в потрібну позицію у сортованій послідовності. Природньо попробувати пришвидшити цей процес, порівнюючи пари елементів, що знаходяться далеко один від одного в масиві. К. Хоор розробив алгоритм Quick Sort із середнім часом роботи порядку O(N*lnN).

Припустимо, що перший елемент масиву, що сортується, є хорошим наближенням елемента, який вкінці опиниться на своєму місці у відсортованій послідовності. Приймемо його значення в якості ведучого елемента, відносно якого ключі будуть мінятися місцями. Для зручності реалізації алгоритму використаємо два вказівники I, J, перший з яких вестиме відлік вздовж розглядуваної частини масиву зліва, а другий - справа. Початково їх значення будуть відповідно I=1, J=N. Таким чином ведучим елементом буде значення a[I]. Перестановки ключів проводяться за такими принципами :

1) порівнюються елементи a[I] та a[J]; якщо a[I]£a[J], то здійснюється крок вліво J:=J-1 і порівняння повторюється; зменшення J продовжується доти, поки не виконається умова a[I]> a[J];

2) якщо при порівнянні елементів досягнута умова a[I]> a[J], то проводиться обмін місцями кючів a[I] та a[J] і здійснюється крок вправо I:=I+1; таким чином ведучий елемент перейшов в позицію J; порівняння ключів із збільшенням I продовжується доти, поки знову не виконається умова a[I]> a[J];

3) у випадку виконання умови a[I]> a[J] проводиться обмін місцями кючів a[I] та a[J] і здійснюється крок вліво J:=J-1; при цьому ведучий елемент знову повертається в позицію I.

Цей процес із почерговим зменшенням J та збільшенням I повторюється з обох кінців послідовності до "середини"до тих пір, поки не досягнеться I=J.

Тепер мають місце два факти. По-перше, ключ, що був першим у вихідній послідовності, в результаті такого впорядкування опиняється на "своєму" місці. По-друге, всі елементи зліва будуть меншими за нього, а всі ключі справа - більшими.

Ту ж саму процедуру можна використати для впорядкування лівої і правої підпослідовностей і т. д. до повного сортування всьго масиву. Таким чином розглянутий алгоритм має чітко виражений рекурсивний характер. Виходячи з цього, значення індексів крайніх елементів меншої з двох невідсортованих підпослідовностей варто помістити в стекову структуру даних, і приступити до впорядкування більшої підпослідовності.

Оскільки короткі послідовності скоріше сортуються при допомозі прямих методів, то алгоритм Quick Sort матиме вхідний параметр - деяке число S, що визначає нижню межу його використання. Провівши нескладний математичний аналіз нерівності, яка пов’язує ефективності алгоритму Quick Sort та прямих алгоритмів сортування

,

можна встановити значення числа S, яке буде нижньою межею використання швидкого сортування. Остання нерівність дає результат .

Однак, якщо крім основних операцій порівняння ключів ще враховувати порівняння індексів та перестановки елементів, то це значення можна збільшити в 2-3 рази.

В якості прикладу наводиться програмна реалізація цього алгоритму у вигляд процедури Quick_Sort. В ній використовується два масиви left і right, де зберігатимуться індексні номери відповідно лівої і правої границь підпослідовностей, які ще будуть впорядковуватися на наступних етапах.

 

Procedure Quick_Sort;

Const S=20;

Var

k, L, R, i, j : integer;

x : basetype;

left, right : array [1..N] of integer;

Begin

k:=1; left[k]:=1; right[k]:=N;

while k>0 do

begin

L:=left[k]; R:=right[k]; k:=k-1;

while R-L>S do

begin

i:=L; j:=R; x:=a[i];

while j>i do

begin

while x<a[j] do j:=j-1;

if j>i then begin

a[i]:=a[j]; a[j]:=x; i:=i+1

end;

while a[i]<x do i:=i+1;

if j>i then begin

a[j]:=a[i]; a[i]:=x; j:=j-1

end

end;

k:=k+1;

if R-i<=i-L then

begin

left[k]:=i+1; right[k]:=R; R:=i-1

end

else

begin

left[k]:=L; right[k]:=i-1; L:=i+1

end

end;

for i:=L+1 to R do

begin

x:=a[i]; j:=i-1;

while (x<a[j]) and (j>=L) do

begin

a[j+1]:=a[j]; j:=j-1

end;

a[j+1]:=x

end

end

End;

 

Аналіз алгоритму Quick Sort. Щоб оцінити ефективність алгоритму, позначимо через Q(N) середню кількість кроків, необхідних для впорядкування N елементів. Припустимо також, S=1, тобто не використовується сортування прямими методами на коротких послідовностях.

При першому проходженні Quick Sort порівнює всі елементи з ведучим і виконується не більше ніж за C*N кроків, де C - деяка константа. Потім потрібно відсортувати дві підпослідовності довжинами I-1 та N-I. Тому середня кількість кроків, потрібних для впорядкування N елементів, залежить від середньої кількості кроків, потрібних для впорядкування I-1 та N-I елементів відповідно. Оскільки всі можливі значення  є рівноймовірними, то спрведлива наступна оцінка :

.

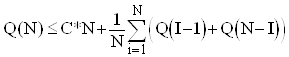Врахувавши, що

,

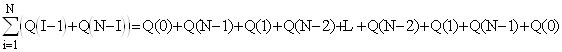отримаємо

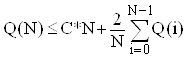.(1)

Покажемо за індукцією по N, що  для , де K=2C+2B, B=Q(0)=Q(1). Останнє співвіднощення означає, що Quick Sort вимагає постійної однакової кількості кроків для впорядкування 0 або 1 елемента.

1) N=2 :  ;

2) припустимо, що  для I=2, 3, ..., N-1 ;

3) перевіримо справедливість для I=N. Співвідношення (1) з врахуванням попереднього припущення можна переписати у вигляді

 або

.(2)

Оскільки функція I*ln(I) є опуклою вниз, то для цілих значень аргументу справедлива оцінка

 

Врахувавши останню нерівність, із співвідношення (2) одержимо

.

Оскільки , то

.

Остаточно отримаємо

.(3)

Таким чином ефективність алгоритму Quick Sort є величина порядку O(N*ln(N)).

Всі наведені викладки справедливі для аналізу по операціях порівняння. Кількість же перестановок залежить від початкового розміщення елементів у послідовності. Характерно, що для цього методу у випадку зворотньо впорядкованого масиву об’єм переміщень ключів не буде максимальним. Адже на кожному етапі ведучий елемент буде найбільшим і опиниться на своєму місці після першого ж порівняння і перестановки, тобто M=N-1. Максимальна кількість переприсвоєнь ключів співпадатиме з кількістю порівнянь, мінімальна - рівна нулю.

Алгоритм Quick Sort, як і розглянуті прямі методи, описує процес стійкого сортування.