Разность матриц

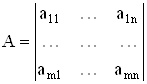
2.2 Разность матриц

Так же, как и сумма, определяется разность двух матриц

Операция нахождения разности двух матриц называется вычитанием матриц. Проверкой можно убедиться, что операция сложения матриц удовлетворяет следующим свойствам:

А + В = В + А; (коммутативность)

А + (В + С) = (А + В) + С; (ассоциативность)

А + О = А.

Здесь А, В, С – произвольные матрицы одинаковых размеров; О – нулевая матрица того же размера.

2.3 Умножение матрицы на число λ

Произведением матрицы А = [аij] на число λ называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением их на число λ. Произведение обозначим λА. Таким образом от умножения матрицы (1) на число, получим:

, то

Проверкой можно убедиться, что операция умножения матрицы на число удовлетворяет следующим свойствам:

1) А = А;

2) (λ + μ)А = λА + μΑ;

3) λ(А + В) = λΑ+ λВ;

4) λ( μА) = (λμ)А;

5) А + (-А) = О.

Здесь А, В – произвольные матрицы; μ, λ - произвольные числа; О – нулевая матрица.

2.4 Умножение матриц

Произведение АВ матрицы А на матрицу В определяется только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. Пусть матрицы А и В такие, что число столбцов матрицы А равно числу строк матрицы В:

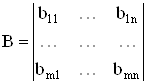
В этом случае произведением матрицы А на матрицу В, которые заданы в определенном порядке (А – 1ая, В – 2ая), является матрица С, элемент которой сij определяется по следующему правилу:

cij = ai1b1j + ai2b2j + … + ainbnj = ∑ n α = 1 aiαbαj,

где i = 1,2, …, m; j = 1, 2, …, k.

Для получения элемента сij матрицы произведения С = АВ нужно элементы i-й строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить.

Число строк матрицы С = АВ равно числу строк матрицы А, а число столбцов – числу столбцов матрицы В.

Умножение матриц некоммутативно, т.е.

АВ ≠ ВА.

Проверкой можно показать, что умножение матриц удовлетворяет следующим свойствам:

1) А(ВС) = (АВ)С; (ассоциативность);

2) λ(АВ) = (λА)В = А(λВ);

3) А(В + С) = АВ + АС. (дистрибутивность).

Здесь А, В, С – матрицы соответствующих определению умножения матриц размеров; λ - произвольное число.

Операция умножения двух прямоугольных матриц распространяется на случай, когда число столбцов в 1ом множителе равно числу строк во 2ом, в остальных случаях произведение не определяется. А также, если матрицы А и В – квадратные одного и того же порядка, то умножение матриц всегда выполнимо при любом порядке следования сомножителей.

2.5 Транспонирование матрицы

Транспонированием матрицы называется такое преобразование матрицы, при котором строки и столбцы меняются ролями при сохранении номеров. Транспонированная матрица обозначается АТ.

.

Для квадратной матрицы это преобразование эквивалентно симметричному отображению относительно главной диагонали.

3 Функциональные модели и блок-схемы решения задачи

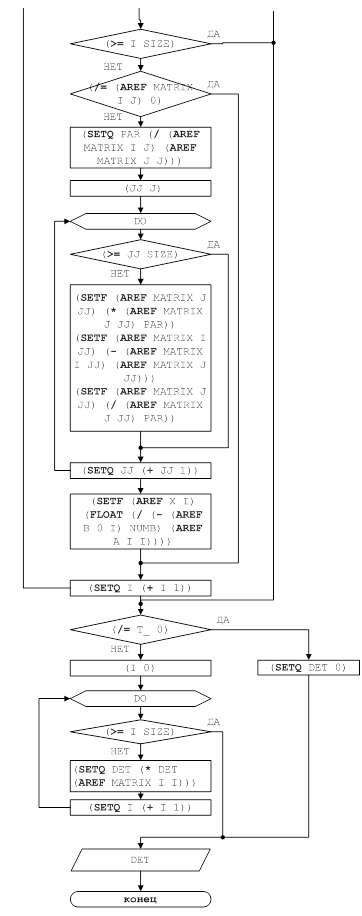
Функциональные модели и блок-схемы решения задачи представлены на рисунках 1 – 7.

Условные обозначения:

MATRIX1 – первая матрица;

MATRIX2 – вторая матрица;

ROW1, R1 – количество строк в первой матрице;

ROW2, R2 – количество строк во второй матрице;

COL1, C1 – количество столбцов в первой матрице;

COL2, C2 – количество столбцов во второй матрице;

RES_MATRIX – результирующая матрица;

OUTPUT_STREAM – выходной поток;

I, J P – рабочие переменные.

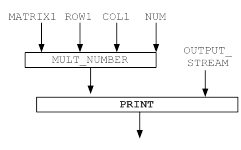
Рисунок 1 – Функциональная модель решения задачи для функции MODUL1

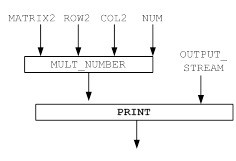
Рисунок 2 – Функциональная модель решения задачи для функции MODUL2

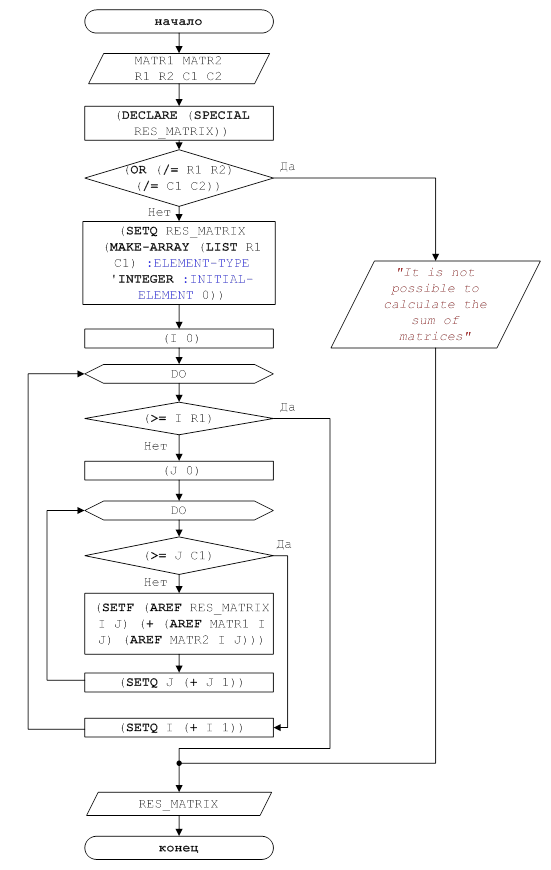
Рисунок 3 – Блок-схема решения задачи для функции SUM_MATRIX

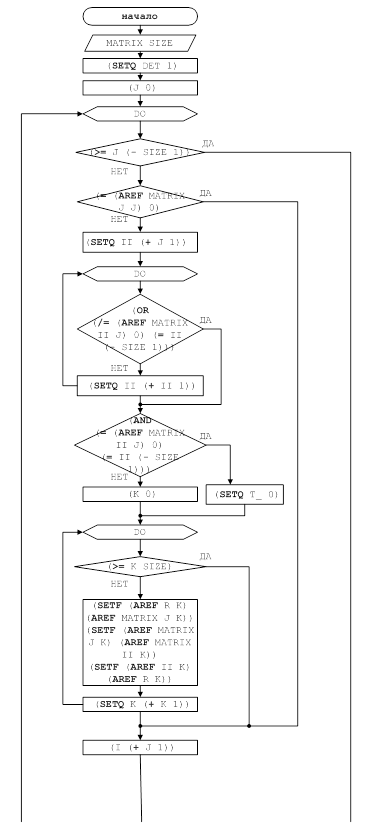
Рисунок 4 – Блок-схема решения задачи для функции SUBTR_MATRIX

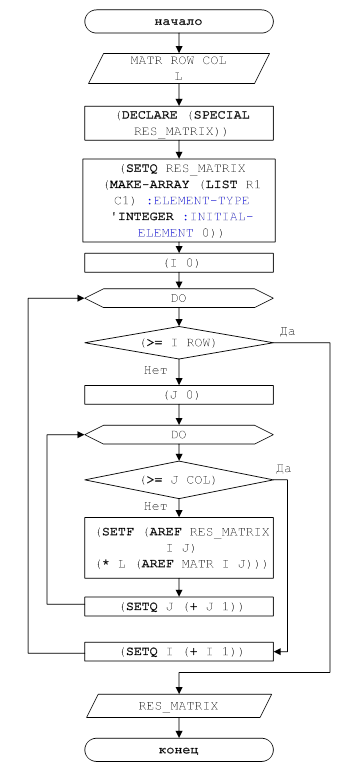
Рисунок 5 – Блок-схема решения задачи для функции MULT_NUMBER

Рисунок 6 – Блок-схема решения задачи для функции MULT_MATRIX

Рисунок 7 – Блок-схема решения задачи для функции FLIP