Навигация
Описание работы программы
1.2 Описание работы программы
Программа составлена для общего случая. В первую матрицу вводятся ее члены в обычных дробях. Программа переводит эти дроби в десятичные и составляет каноническую форму. Затем происходит процесс формирования первой симплекс таблицы.
Следующим этапом программа начинает составлять итерации, до тех пор пока не будет найдено оптимальное решение (в данном случае составлено 2 итерации).
Программа выводит данные в строку F/
1.3 Листинг программы
//-------------------------------------------------------------------------------------------
#include <stdio.h>
#include <string.h>
#include <math.h>
#define PRECISION "%6.2f" // формат вывода дробных чисел
#define PRECISION2 "%.2f" // он же только целая часть любой длины
#define MAXDIGIT 1000000 // должно быть очень большое число (больше всех)
typedef enum
{
NEXT_ITERATION, // нужно продолжать итерации
PLAN_OPTIMAL, // найден оптимальный опорный план
ODR_BREAK, // ОДР разомкнута
ODR_EMPTY, // ОДР пустая
DUAL_DONE /* первый этап (построение опорного плана) окончен,
переходим к поиску оптим.оп.плана (обычный Симплекс) */
} plan_t;
int cn=0; // длина вектора исходного ур-я
int cnr=0; /* cn, только без членов == 0 (cnr==cn_real)
нужно только для вывода сокращенной таблицы */
float *c = NULL; // исходное ур-е
int m=0, n=0; // размеры матрицы условий
float **a = NULL; // матрица условий
float *b = NULL; // столбец свободных членов матрицы условий
int *base = NULL; // базовые переменные
float zb=0; // оценки оптимальности b
float *za = NULL; // оценки оптимальности a
int base_column = -1; // разрешающий столбец
int base_row = -1; // разрешающая строка
bool full_table = true; // вид выводимой таблицы: true==полная, false==сжатая
void FreeMem ()
{
delete[] za;
delete[] base;
delete[] b;
for (int i=0; i<m; i++)
delete[] a[i];
delete[] a;
delete[] c;
}
bool ReadInput (char *filename)
{
int i,j;
FILE *f = fopen(filename, "r");
if (NULL == f)
return false;
// исходное ур-е
fscanf(f, "%i", &cn);
c = new float [cn];
cnr=cn;
for (i=0; i<cn; i++)
{
fscanf(f, "%f", &c[i]);
if (0 == c[i]) cnr--;
}
// матрица условий
fscanf(f, "%i %i", &n, &m);
a = new float* [m];
for (i=0; i<m; i++)
a[i] = new float[n];
b = new float [m];
for (j=0; j<m; j++)
{
for (i=0; i<n; i++)
fscanf(f, "%f", &a[j][i]);
fscanf(f, "%f", &b[j]);
}
// базовые переменные
base = new int [m];
for (j=0; j<m; j++)
{
fscanf(f, "%i", &base[j]);
--base[j];
}
// флаг - полную или сжатую таблицу выводить ?
int flag = 1;
fscanf(f, "%i", &flag);
full_table = flag ? true : false;
fclose(f);
za = new float[n];
// for(i=0;i<n;i++)za[i]=0;// !!! только для отладки !!!
return true;
}
// Вычисление оценок оптимальности {za==delta_j[] and zb==Z}
void EvaluationOptimal ()
{
int i,j;
zb=0;
for (i=0; i<n; i++) za[i]=0;
for (j=0; j<m; j++)
{
for (i=0; i<n; i++)
za[i] += c[base[j]]*a[j][i];
zb += c[base[j]]*b[j];
}
for (i=0; i<n; i++)
za[i] -= c[i];
}
// Построение опорного плана (этот этап только в двойственном симплекс-методе)
plan_t BuildPsevdoPlan ()
{
int i,j;
base_column = -1; // разрешающий столбец
base_row = -1; // разрешающая строка
float acc; // временно: аккумулятор - будет хранить min, max, etc.
acc = 0; // min отрицательное значение b
for (j=0; j<m; j++)
if (b[j] < acc)
{
acc = b[j];
base_row = j;
}
if (-1 == base_row)
return DUAL_DONE;
acc = -MAXDIGIT; // max отношение za к отрицат. эл-там в строке base_row
for (i=0; i<n; i++)
{
float temp;
if (a[base_row][i] < 0 && (temp = za[i]/a[base_row][i]) > acc)
{
acc = temp;
base_column = i;
}
}
if (-1 == base_column)
return ODR_EMPTY;
return NEXT_ITERATION;
}
// Проверка опорного плана на оптимальность
plan_t CheckStrongPlan ()
{
int i,j;
float za_min = 0;
base_column = -1; // разрешающий столбец
base_row = -1; // разрешающая строка
// выбор разрешающего столбца
for (i=0; i<n; i++)
{
if (za[i] >= 0)
continue;
else if (za[i] < za_min)
{
za_min = za[i];
base_column = i;
}
}
if (-1 == base_column)
return PLAN_OPTIMAL;
za_min = MAXDIGIT;
// выбор разрешающей строки
for (j=0; j<m; j++)
{
if (a[j][base_column] > 0)
{
float t = b[j]/a[j][base_column];
if (t < za_min)
{
za_min = t;
base_row = j;
}
}
}
if (-1 == base_row)
return ODR_BREAK;
return NEXT_ITERATION;
}
// Преобразование таблицы по ф-лам Жордана-Гаусса
void JGTransformation (int base_row, int base_column)
{
// проверка на всякий случай: чтобы не было деления на нуль
if (0 == a[base_row][base_column]) return;
base[base_row] = base_column;
int i,j;
float **a2 = new float* [m]; // матрица условий
float *b2 = new float [m]; // столбец свободных членов матрицы условий
memcpy(b2,b,m*sizeof(float));
for (j=0; j<m; j++)
{
a2[j] = new float[n];
memcpy(a2[j],a[j],n*sizeof(float));
}
for (j=0; j<m; j++)
{
for (i=0; i<n; i++)
{
if (i == base_column)
{
a2[j][i] = (float) (j == base_row ? 1 : 0);
}
else
{
if (j == base_row)
a2[j][i] = a[j][i]/a[base_row][base_column];
else
a2[j][i] = a[j][i] - a[base_row][i]*a[j][base_column]/
a[base_row][base_column];
}
}
if (j == base_row)
b2[j] = b[j]/a[base_row][base_column];
else
b2[j] = b[j] - b[base_row]*a[j][base_column]/
a[base_row][base_column];
}
memcpy(b,b2,m*sizeof(float));
delete[] b2;
for (j=0; j<m; j++)
{
memcpy(a[j],a2[j],n*sizeof(float));
delete[] a2[j];
}
delete[] a2;
}
// проверка: входит ли номер столбца в число базисных переменных
bool InBase (int num)
{
for (int j=0; j<m; j++)
if (num == base[j])
return true;
return false;
}
// вывод линии символов
void Rule (char c, int amount = full_table ? 5+(n+2)*8 : 5+(cnr+1)*8)
{
for (int i=0; i<amount; i++)
printf("%c", c);
printf("\n");
}
// вывод Симплекс-таблицы
void ShowTable ()
{
int i,j;
static int iteration = 0;
printf("[%i]\n", iteration++);
if (full_table)
// полная таблица
{
Rule('=');
printf("Баз.| | |");
for (i=0; i<cn; i++)
printf(PRECISION " |", c[i]);
printf("\nпер.| Ci | Bi |");
Rule('-', n*8);
printf(" | | |");
for (i=0; i<cn; i++)
printf(" x%i |", i+1);
printf("\n");
Rule('=');
for (j=0; j<m; j++)
{
printf(" x%i |" PRECISION " |" PRECISION " |",
base[j]+1, c[base[j]], b[j]);
for (i=0; i<n; i++)
printf(PRECISION "%c|", a[j][i],
base_column == i && base_row == j ?'*':' ');
printf("\n");
}
Rule('=');
printf(" Z | --- |" PRECISION " |", zb);
for (i=0; i<n; i++)
printf(PRECISION " |", za[i]);
printf("\n");
Rule('-');
}
else
// сжатая таблица
{
Rule('=');
printf("БvС>|");
for (i=0; i<cn; i++)
{
if (!InBase(i))
printf(" x%i |", i+1);
}
printf(" Bi |\n");
Rule('=');
for (j=0; j<m; j++)
{
printf(" x%i |", base[j]+1);
for (i=0; i<n; i++)
{
if (!InBase(i))
printf(PRECISION "%c|", a[j][i],
base_column == i && base_row == j ?'*':' ');
}
printf(PRECISION" |\n", b[j]);
}
Rule('=');
printf(" Z |");
for (i=0; i<n; i++)
{
if (!InBase(i))
printf(PRECISION " |", za[i]);
}
printf(PRECISION " |\n", zb);
Rule('-');
}
if (base_column > -1 && base_row > -1)
printf("Разрешающий столбец:%2i\nРазрешающая строка: %2i\n\nX=(",
base_column+1, base_row+1);
else
printf("\nX=(");
for (i=0; i<n; i++)
{
int basen = -1;
for (j=0; j<m; j++)
if (base[j] == i) {basen = j; break;}
printf(PRECISION2 "%c ", -1==basen?0:b[basen], i!=n-1?',':')');
}
printf("\nZ=" PRECISION2 "\n\n\n", zb);
}
int main (int argc, char *argv[])
{
if (argc < 2)
{
printf("Missing argument\n");
return -1;
}
if (!ReadInput(argv[1]))
{
printf("Error open file %s.\n", argv[1]);
return -1;
}
printf("*** ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД ***\n\n");
plan_t plan;
bool dual_done = false;
for (int k=0; k<2*m+1; k++)
{
if (k) JGTransformation(base_row, base_column);
EvaluationOptimal();
if (dual_done)
{
plan = CheckStrongPlan();
}
else
{
plan = BuildPsevdoPlan(); // only in dual-simplex
if (DUAL_DONE == plan)
{
dual_done = true;
plan = CheckStrongPlan();
}
}
ShowTable();
if (NEXT_ITERATION != plan)
{
char *s;
switch (plan)
{
case PLAN_OPTIMAL: s="Опорный план оптимальный"; break;
case ODR_BREAK: s="Область допустимых решений разомкнутая"; break;
case ODR_EMPTY: s="Область допустимых решений пустая"; break;
}
printf("\n%s.\n", s);
break;
}
}
FreeMem();
return 0;
}
//-----------------------------------------------------------------------------------------
Результат работы программы
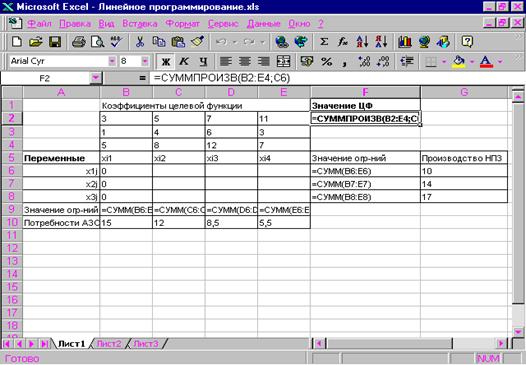
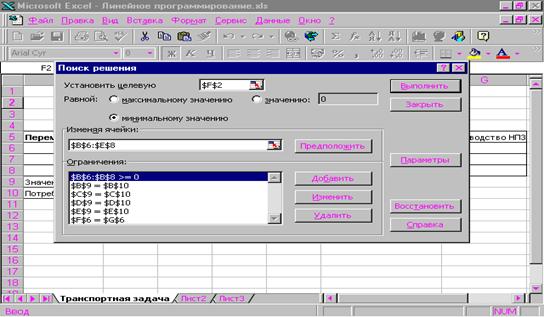
Работу программы мы можем проанализировать по результату . Здесь мы видим первоначальную матрицу, которая представлена в виде симплекс таблицы и результат преобразования таблицы. Результат преобразования таблицы представлен в виде симплекс таблицы, подобной первоначальной.
Проанализировав данные полученные с помощью программы и сравнив их с результатами вычислений можно сделать вывод, что полученные результаты равны между собою, а это значит что программа работает верно.
Похожие работы
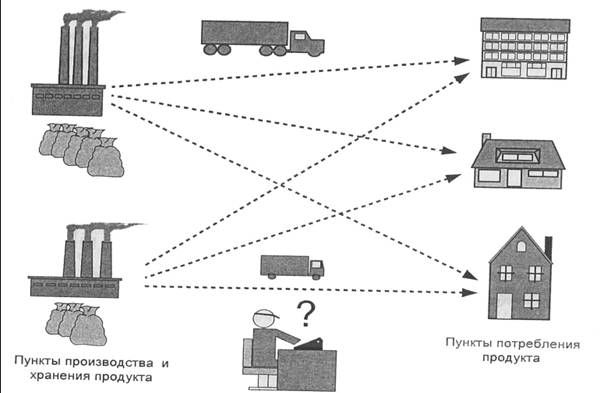
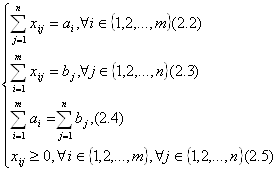
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... среди математиков, его разделяли А.Н.Колмогоров, И.М.Гельфанд, В.И.Арнольд, С.П.Новиков и др. Нельзя не восхищаться естественностью и внутренней стройностью математической работ Л.В. по двойственности линейного программирования и их экономической интерпретацией. 2. О математической экономике как области математики и о некоторых ее связях А) Связи линейного программирования с функциональным и ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... области (если допустимая область ограничена и не пуста); 3. ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи. Гл 2 Решение задач линейного программирования графическим способом на ЭВМ 2.1 Описание работы программы Программа написана с использованием собственных функций и процедур и трех стандартных модулей System, Crt и ...

0 комментариев