Навигация
Симплекс метод решения задач линейного программирования
2 Симплекс метод решения задач линейного программирования
Симплекс метод - универсальный метод для решения линейной системы уравнений или неравенств и линейного функционала.
Для привидения системы ограничений неравенств к каноническому виду, необходимо в системе ограничений выделить единичный базис.
I. Ограничения вида «»- ресурсные ограничения. Справа находится то что мы используем на производстве, слева - то что получаем. При таких ограничения вводят дополнительные переменные с коэффициентом «+1», образующие единичный базис. В целевую функцию эти переменные войдут с коэффициентом «0».
II. Ограничения вида «=». Часто бывает, что несмотря на то что ограничения имеют вид равенства, единичный базис не выделяется или трудно выделяется. В этом случае вводятся искусственные переменные для создания единичного базиса - Yi. В систему ограничений они входят с коэффициентом «1» , а в целевую функцию с коэффициентом «M», стремящимся к бесконечности (при Fmin - «+M», при Fmax - «-M»).
III. Ограничения вида «» - Плановые ограничения. Дополнительные переменные (X), несущие определенный экономический смысл - перерасход ресурсов или перевыполнение плана, перепроизводство, добавляются с коэффициентом «-1», в целевую функцию - с коэффициентом «0». А искусственные переменные (Y) как в предыдущем случае.
Алгоритм симплекс метода.
(первая симплекс таблица)
![]() Пусть система приведена к каноническому виду.
Пусть система приведена к каноническому виду.
X1+ q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h1
X2+ q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h1
X3+ q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h1
……………………………………………………………….
Xm+ qm,m+1 Xm+1 + …. + qm,m+n Xm+n =hm
В ней m базисных переменных, k свободных переменных. m+k=n - всего переменных.
Fmin= C1X1+ C2X2+ C3X3+....+ CnXn
Все hi должны быть больше либо равны нулю, где i=1,2...m. На первом шаге в качестве допустимого решения принимаем все Xj=0 (j=m+1,m+2,...,m+k). При этом все базисные переменные Xi=Hi.
Для дальнейших рассуждений вычислений будем пользоваться первой симплекс таблицей (таблица 3.1).
Таблица 1.
| C | Б | H | C1 | C2 | … | Cm | Cm+1 | … | Cm+k |
| X1 | X2 | … | Xm | Xm+1 | … | Xm+k | |||
| C1 C2 C3 : : Cm | X1 X2 X3 : : Xm | h1 h2 h3 : : hm | 1 0 0 : : 0 | 0 1 0 : : 0 | : : : : : : | 0 0 0 : : 0 | q1,m+1 q2,m+1 q3,m+1 : : qm,m+1 | : : : : : : | q1,m+k q2,m+k q3,m+k : : qm,m+k |
| F= | F0 | | | … | m | m+1 | … | m+k |
Первый столбец- коэффициенты в целевой функции при базисных переменных.
Второй столбец - базисные переменные.
Третий столбец - свободные члены (hi0).
Самая верхняя строка - коэффициенты при целевой функции.
Вторая верхняя строка - сами переменные, входящие в целевую функцию и в систему ограничений.
Основное поле симплекс метода - система коэффициентов из уравнения.
Последняя строка - служит для того, чтобы ответить на вопрос: «оптимален план или нет».
Для первой итерации F0= ci*hi.
m - оценки они рассчитываются по формуле:
j = ciqij-cj.
Индексная строка позволяет нам судить об оптимальности плана:
1. При отыскании Fmin в индексной строке должны быть отрицательные и нулевые оценки.
2. При отыскании Fmax в индексной строке должны быть нулевые и положительные оценки.
Переход ко второй итерации:
Для этого отыскиваем ключевой (главный) столбец и ключевую (главную) строку.
Ключевым столбцом является тот в котором находится наибольший положительный элемент индексной строки при отыскании Fmin или наименьший отрицательный элемент при отыскании Fmax.
Ключевой строкой называется та, в которой содержится наименьшее положительное частное от деления элементов столбца H на соответствующие элементы ключевого столбца.
На пересечении строки и столбца находится разрешающий элемент.
На этом этапе осуществляется к переходу к последующим итерациям.
Переход к итерациям:
1. Выводится базис ключевой строки, уступая место переменной из ключевого столбца со своим коэффициентом.
2. Заполняется строка вновь введенного базиса путем деления соответствующих элементов выделенной строки предыдущей итерации на разрешающий элемент.
3. Если в главной строке содержится нулевой элемент, то столбец, в котором находиться этот элемент переноситься в последующую итерацию без изменения.
4. Если в главном столбце имеется нулевой элемент, то строка, в которой он находиться переноситься без изменения в последующую итерацию.
5. Остальные элементы переносятся по формуле:
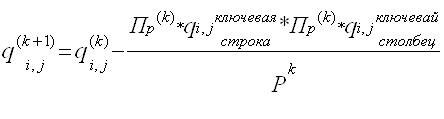
Метод искусственного базиса.(Вторая симплекс таблица)
При использовании искусственного базиса необходимо добиваться выхода искусственных переменных из базиса и введение в него независимых переменных. Для этой цели можно также использовать симплекс метод, причем решение распадается на две фазы:I. Построение искусственного базиса и оптимизация функции суммы искусственных переменных, т.е. F0=Y1+Y2+…+Yn = 0 (Fmin). Если при этом F0=0, то искусственный базис мы вывели из состава переменных, переходим ко второй фазе – решаем задачу по первой симплекс таблице с действительными переменными. Если же F00, т.е. искусственный базис не выведен из состава переменных – ОЗЛП решений не имеет.
II. Решение преобразованной системы ограничений с заданной целевой функцией и действительными переменными. При этом столбцами искусственных переменных в симплекс методе пренебрегаем.
Замечания:
1. При решении задач на max с искусственным базисом следует переходить к решению на min, меняя лишь только целевую функцию:
Fmax = - Fmin.
2. При решении ЗЛП с искусственным базисом особое внимание следует обратить на вычисление элементов индексных строк.
a) Для столбцов X вычисление элементов идет по формулам:
j = qij.
yi = y1+y2+…+yR.
Hi=F0.
Примечание: только для строк Y.
б) Для столбцов Y работает старая формула:
j = ciqij-cj.
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... среди математиков, его разделяли А.Н.Колмогоров, И.М.Гельфанд, В.И.Арнольд, С.П.Новиков и др. Нельзя не восхищаться естественностью и внутренней стройностью математической работ Л.В. по двойственности линейного программирования и их экономической интерпретацией. 2. О математической экономике как области математики и о некоторых ее связях А) Связи линейного программирования с функциональным и ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... области (если допустимая область ограничена и не пуста); 3. ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи. Гл 2 Решение задач линейного программирования графическим способом на ЭВМ 2.1 Описание работы программы Программа написана с использованием собственных функций и процедур и трех стандартных модулей System, Crt и ...

0 комментариев