Навигация
Ограничения на допустимое множество
20533
знака
10
таблиц
1
изображение
2.2. Ограничения на допустимое множество
Теорема Вейерштрасса: непрерывная функция, определённая на непустом замкнутом ограниченном множестве, достигает минимума (максимума) по крайней мере в одной из точек этого множества.
2.3. Классическая задача оптимизации
Состоит в нахождении минимума целевой функции
, где 
– точка в пространстве 
при начальных ограничениях типа равенств
(3)
Если (3) имеют место, то минимум q(x) называется условным минимумом. Если ограничения (3) отсутствуют, то говорят о безусловном минимуме.
Классический способ решения данной задачи состоит в том, что (3) используют для исключения из рассмотрения 
переменных. При этом целевая функция приводится к виду
(4)
,где через 
обозначены неисключаемые переменные. Задача теперь состоит в нахождении значений , которые обращают в минимум q1 и на которые не наложено ограничений (задача на безусловный экстремум).
2.4. Функция Лагранжа
Введём в рассмотрение вектор 
и исследуем свойства функции
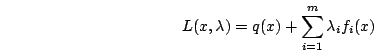(5)
– функция Лагранжа, 
- множители Лагранжа.
– функция n+m переменных 
.
Рассмотрим стационарные точки функции , которые получим, приравняв к нулю частные производные по 
и по 
:
(6)
(7)
Если в стационарной точке (x*, y*) функция достигает минимума, то 
обеспечивает минимум функции q(x) и при выполнении ограничений (3), т.е. даёт решение задачи.
Задача на условный минимум целевой функции q(x) при наличии ограничений типа равенств сводится к задаче на определение стационарных точек функции Лагранжа .
3. Линейное программирование: формулировка задач и их графическое решение
3.1. Задача ЛП
Рассмотрим на примере задачи фирмы Reddy Mikks. Небольшая фабрик изготовляет два вида красок: для наружных (E) и внутренних (I) работ. Продукция поступает в оптовую продажу. Для производства красок используется два исходных продукта – A и B. Максимально возможные суточные запасы этих продуктов составляют 6т и 8т соответственно. Расходы A и B на производство 1т соответствующих красок приведены в таблице.
| Исходный продукт | Расход на тонну краски | Максимальный запас, т. | |
| краска E | краска I | ||
| A | 1 | 2 | 6 |
| B | 2 | 1 | 8 |
Суточный спрос на краску I никогда не превышает спроса на краску E более чем на 1т. Спрос на I не превышает 2т. Оптовая цена за 1т краски E – 3000$, I – 2000$. Какое количество краски каждого вида фабрика должна производить, чтобы доход от реализации продуктов был максимальным?
Так как нужно определить объём производства каждого вида краски, переменными в модели являются:
xE – суточный объём производства краски E (в тоннах);
xI – суточный объём производства краски I (в тоннах).
Обозначив доход (в тыс. $) через 
, можно дать математическую формулировку целевой функции: определить (допустимые) значения xE и xI, максимизирующие величину общего дохода 
Ограничения на расход исходных продуктов:
(для A)
(для B)
Ограничения на величину спроса на продукцию:
Потребуем выполнения условия неотрицательности переменных:
Получили математическую модель:
Определить суточные объёмы производства (в т.) краски I и E, при которых достигается
(целевая функция)
при ограничениях
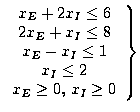
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... среди математиков, его разделяли А.Н.Колмогоров, И.М.Гельфанд, В.И.Арнольд, С.П.Новиков и др. Нельзя не восхищаться естественностью и внутренней стройностью математической работ Л.В. по двойственности линейного программирования и их экономической интерпретацией. 2. О математической экономике как области математики и о некоторых ее связях А) Связи линейного программирования с функциональным и ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... области (если допустимая область ограничена и не пуста); 3. ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи. Гл 2 Решение задач линейного программирования графическим способом на ЭВМ 2.1 Описание работы программы Программа написана с использованием собственных функций и процедур и трех стандартных модулей System, Crt и ...
0 комментариев