Навигация
Силовские подгруппы конечных групп
1. Силовские подгруппы конечных групп
По теореме Лагранжа порядок каждой группы делит порядок конечной группы. Обратное утверждение не всегда верно, т.е. если натуральное число ![]() делит порядок конечной группы
делит порядок конечной группы ![]() , то в группе
, то в группе ![]() может и не быть подгруппы порядка
может и не быть подгруппы порядка ![]() .
.
Пример 1.1 Знакопеременная группа ![]() порядка 12 не содержит подгруппу порядка 6.
порядка 12 не содержит подгруппу порядка 6.
Допустим противное, пусть ![]() – подгруппа порядка 6 в группе
– подгруппа порядка 6 в группе ![]() . Тогда
. Тогда ![]() и
и ![]() . Группа
. Группа ![]() содержит подгруппы
содержит подгруппы
![]()
Если ![]() , то
, то ![]() и
и ![]() , противоречие. Поэтому
, противоречие. Поэтому ![]() , а т. к.
, а т. к. ![]() , то
, то ![]() . Противоречие. Поэтому допущение не верно и группа
. Противоречие. Поэтому допущение не верно и группа ![]() не содержит подгруппу порядка 6.
не содержит подгруппу порядка 6.
Вполне естественно возниает вопрос: для каких делителей ![]() порядка конечной группы имеется подгруппа порядка
порядка конечной группы имеется подгруппа порядка ![]() .
.
Положительный ответ на этот вопросв случае, когда ![]() – степень простого числа, даёт теорема Силова. Для доказательства теоремы Силова потребуется следующая лемма.
– степень простого числа, даёт теорема Силова. Для доказательства теоремы Силова потребуется следующая лемма.
Лемма 1.2 Если порядок конечной абелевой группы ![]() делится на простое число
делится на простое число ![]() , то в группе
, то в группе ![]() существует элемент порядка
существует элемент порядка ![]() .
.
Доказательство. Предположим противное, т.е. допустим, что существует абелева группа ![]() порядка
порядка ![]() , простое число
, простое число ![]() делит
делит ![]() , то в группе
, то в группе ![]() существует элемент порядка
существует элемент порядка ![]() . Пусть
. Пусть ![]() .
.
Если ![]() делит
делит ![]() для некоторого
для некоторого ![]() , то
, то ![]() – элемент порядка
– элемент порядка ![]() , противоречие. Поэтому все элементы группы
, противоречие. Поэтому все элементы группы ![]() имеют порядки, не делящиеся на
имеют порядки, не делящиеся на ![]() .
.
![]()
не делится на ![]() .
.
Так как группа ![]() абелева, то
абелева, то ![]() – подгруппа, и к произведению
– подгруппа, и к произведению ![]() можно применить следующее
можно применить следующее
![]()
не делится на ![]() .
.
Затем ![]() обозначаем через
обозначаем через ![]() и опять получаем, что
и опять получаем, что ![]() не делится на
не делится на ![]() . Через конечное число шагов приходим к выводу, что
. Через конечное число шагов приходим к выводу, что ![]() не делится на
не делится на ![]() . Но
. Но
![]()
и ![]() , т.е. получаем, что
, т.е. получаем, что ![]() не делит
не делит ![]() . Противоречие. Значит, допущение неверно и лемма спарведлива.
. Противоречие. Значит, допущение неверно и лемма спарведлива.
Пусть ![]() – простое число.
– простое число. ![]() - Группой называют конечную группу, порядок которой есть степень числа
- Группой называют конечную группу, порядок которой есть степень числа ![]() . Конечная группа называется примарной, если она является
. Конечная группа называется примарной, если она является ![]() -группой для некоторого простого
-группой для некоторого простого ![]() .
.
Теорема 1.3 Ошибка!. Пусть конечная группа ![]() имеет порядок
имеет порядок ![]() , где
, где ![]() – простое число и
– простое число и ![]() не делит
не делит ![]() . Тогда спарведливы следующие утверждения:
. Тогда спарведливы следующие утверждения:
в группе ![]() существует подгруппа порядка
существует подгруппа порядка ![]() для каждого
для каждого ![]() ;
;
если ![]() –
– ![]() -подгруппа группы
-подгруппа группы ![]() и
и ![]() – подгруппа порядка
– подгруппа порядка ![]() , то существует такой элемент
, то существует такой элемент ![]() , что
, что ![]() ;
;
любые две подгруппы порядка ![]() сопряжены в группе
сопряжены в группе ![]() ;
;
число подгрупп порядка ![]() в группе
в группе ![]() сравнимо с единицей по модулю
сравнимо с единицей по модулю ![]() и делит
и делит ![]() .
.
Доказательство. Доказательство проведём индукцией по ![]() . По индукции считаем, что для всех групп, порядок которых меньше порядка
. По индукции считаем, что для всех групп, порядок которых меньше порядка ![]() утверждение теоремы выполняется. Рассмотрим два случая.
утверждение теоремы выполняется. Рассмотрим два случая.
Случай 1. Порядок центра ![]() делится на
делится на ![]() .
.
Так как ![]() – абелева группа, то к
– абелева группа, то к ![]() применима лемма 1.2. По этой лемме в
применима лемма 1.2. По этой лемме в ![]() есть элемент
есть элемент ![]() порядка
порядка ![]() . Так как
. Так как ![]() – нормальная подгруппа группы
– нормальная подгруппа группы ![]() порядка
порядка ![]() , то факторгруппа
, то факторгруппа ![]() имеет порядок
имеет порядок ![]() и по индукции в группе
и по индукции в группе ![]() имеется подгруппа
имеется подгруппа ![]() порядка
порядка ![]() для каждого
для каждого ![]() . По теореме о соответствии в группе
. По теореме о соответствии в группе ![]() имеется подгруппа
имеется подгруппа ![]() такая, что
такая, что ![]() и
и ![]() . Теперь
. Теперь ![]() , где
, где ![]() . Итак, в группе
. Итак, в группе ![]() порядков
порядков ![]() соответственно.
соответственно.
Случай 2. Порядок центра ![]() группы
группы ![]() не делится на
не делится на ![]() .
.
Рассмотрим разложение группы ![]() в объдинение различных классов сопряжённых элементов
в объдинение различных классов сопряжённых элементов
![]()
где
![]()
– класс сопряжённых с ![]() элементов. Различные классы сопряжённых элементов имеют пустое пересечение, а число элементов в классе
элементов. Различные классы сопряжённых элементов имеют пустое пересечение, а число элементов в классе ![]() равно индексу централизатора
равно индексу централизатора ![]() . Пусть
. Пусть
![]()
Централизатор каждого элемента из центра совпадает с группой ![]() . И обратно, если централизатор некоторого элемента совпадает с группой, то элемент попадает в центр
. И обратно, если централизатор некоторого элемента совпадает с группой, то элемент попадает в центр ![]() . Поэтому из <1> получаем
. Поэтому из <1> получаем
![]()
где ![]() для каждого
для каждого ![]() . Если все числа
. Если все числа ![]() делятся на
делятся на ![]() , то из <2> следует, что
, то из <2> следует, что ![]() делится на
делится на ![]() , что противоречит рассматриваемому случаю. Итак, существует
, что противоречит рассматриваемому случаю. Итак, существует ![]() , где
, где ![]() такое, что
такое, что ![]() не делит
не делит ![]() . Поскольку
. Поскольку ![]() то
то
![]()
где ![]() – целое число и
– целое число и ![]() не делит
не делит ![]() . Теперь к группе
. Теперь к группе ![]() применима индукция. По индукции в группе
применима индукция. По индукции в группе ![]() существует подгруппа порядка
существует подгруппа порядка ![]() для каждого
для каждого ![]() Эта подгруппа будет искомой для группы
Эта подгруппа будет искомой для группы ![]() .
.
Рассмотрим разложение группы ![]() на двойные смежные классы по подгруппам
на двойные смежные классы по подгруппам ![]() и
и ![]() :
:
![]()
Зададим отображение
![]()
переводящее элементы двойного смежного класса ![]() в элементы произведения подгрупп
в элементы произведения подгрупп ![]() и
и ![]() . Легко проверить, что отоюражение
. Легко проверить, что отоюражение ![]() взаимно однозначно, поэтому, получаем
взаимно однозначно, поэтому, получаем

где ![]() Так как
Так как ![]() есть подгруппа в
есть подгруппа в ![]() , то по теореме Лагранжа
, то по теореме Лагранжа ![]() делит
делит ![]() и
и ![]() – целое число. Из <3> теперь получаем:
– целое число. Из <3> теперь получаем:
![]()
Сокращая обе части на ![]() получим:
получим:
![]()
Так как ![]() взаимно просто с
взаимно просто с ![]() , а
, а ![]() – целое число, являющееся степенью
– целое число, являющееся степенью ![]() , то в правой части <4> существует слагаемое, равное единице. Пусть например,
, то в правой части <4> существует слагаемое, равное единице. Пусть например, ![]() , где
, где ![]() . Тогда
. Тогда ![]() .
.
Пусть ![]() и
и ![]() – подгруппы порядка
– подгруппы порядка ![]() . По существует элемент
. По существует элемент ![]() такой, что
такой, что ![]() . Так как
. Так как ![]() , то
, то ![]() .
.
Пусть ![]() – группа порядка
– группа порядка ![]() – подгруппа порядка
– подгруппа порядка ![]() и
и ![]() – нормализатор подгруппы
– нормализатор подгруппы ![]() в группе
в группе ![]() . Рассмотрим разложение группы
. Рассмотрим разложение группы ![]() на двойные смежные классы по
на двойные смежные классы по ![]() и
и ![]() :
:
![]()
Отображение
![]()
будет взаимно однозначным отображением ![]() на
на ![]() . Теперь из <5> получаем:
. Теперь из <5> получаем:
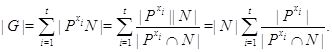
Положим ![]() . Элемент
. Элемент ![]() можно выбрать единичным, поэтому
можно выбрать единичным, поэтому ![]() и
и ![]() . Теперь
. Теперь
![]()
Проверим, что под знаком суммы нет слагаемых равных 1. Допустим противное, т.е. что для некоторого ![]() имеем равенство
имеем равенство ![]() . Это означает, что
. Это означает, что ![]() и подгруппа
и подгруппа ![]() содержит две подгруппы
содержит две подгруппы ![]() и
и ![]() порядка
порядка ![]() . По существует элемент
. По существует элемент ![]() такой, что
такой, что ![]() . Но тогда
. Но тогда ![]() , а так как
, а так как ![]() , то и
, то и ![]() . Но это возможно только при
. Но это возможно только при ![]() , противоречие. Значит, допущение неверно и в равенстве <6> под знаком суммы все слагаемые отличны от единицы. Поскольку каждое слагаемое есть степень простого
, противоречие. Значит, допущение неверно и в равенстве <6> под знаком суммы все слагаемые отличны от единицы. Поскольку каждое слагаемое есть степень простого ![]() , то из равенства <6> получаем сравнение
, то из равенства <6> получаем сравнение ![]()
![]() . По все подгруппы порядка
. По все подгруппы порядка ![]() группы
группы ![]() сопряжены между собой, а число подгрупп сопряжённых с
сопряжены между собой, а число подгрупп сопряжённых с ![]() равно
равно ![]() . Поскольку
. Поскольку ![]() , то
, то ![]() делит
делит ![]() .
.
Теорема доказана.
Силовской ![]() – подгруппой конечной группы
– подгруппой конечной группы ![]() называют такую
называют такую ![]() – подгруппу, индекс которой не делится на
– подгруппу, индекс которой не делится на ![]() . Непосредственно из теоремы получаем
. Непосредственно из теоремы получаем
Следствие 1.4 Пусть конечная группа ![]() имеет порядок
имеет порядок ![]() , где
, где ![]() – простое число и
– простое число и ![]() не делит
не делит ![]() . Тогда:
. Тогда:
существует силовская ![]() –подгруппа и её порядок равен
–подгруппа и её порядок равен ![]() ;
;
каждая ![]() –подгруппа содержится в некоторой силовской
–подгруппа содержится в некоторой силовской ![]() –подгруппе;
–подгруппе;
любые две силовские ![]() –подгруппы сопряжены;
–подгруппы сопряжены;
число силовских ![]() –подгрупп сравнимо с единицей по модулю
–подгрупп сравнимо с единицей по модулю ![]() и делит
и делит ![]() .
.
Теорема 1.5 Для конечной группы ![]() и её силовской
и её силовской ![]() –подгруппы
–подгруппы ![]() справедливы следующие утверждения:
справедливы следующие утверждения:
если ![]() , то
, то ![]() – силовская
– силовская ![]() –подгруппа в
–подгруппа в ![]() , а
, а ![]() – силовская
– силовская ![]() –подгрупппа в
–подгрупппа в ![]() ;
;
![]() ;
;
если ![]() и
и ![]() , то
, то
![]()
и
![]()
пусть ![]() – все простые делители порядка группы
– все простые делители порядка группы ![]() ,
, ![]() при
при ![]() , и пусть
, и пусть ![]() – соответствующие им силовские подгруппы. Тогда
– соответствующие им силовские подгруппы. Тогда
![]()
а если ![]() , то
, то ![]() .
.
Д о к а з а т.е. л ь с т в о. Так как ![]() и
и ![]() не делит
не делит ![]() , то
, то ![]() –
– ![]() –группа, а из того, что
–группа, а из того, что
![]()
следует
![]()
![]()
и ![]() не делится на
не делится на ![]() . Значит
. Значит ![]() – силовская
– силовская ![]() –подгруппа в
–подгруппа в ![]() .
.
Поскольку ![]() , то
, то ![]() –
– ![]() –группа, а так как
–группа, а так как
![]()
не делится на ![]() , то
, то ![]() – силовская
– силовская ![]() –подгруппа в
–подгруппа в ![]() .
.
Для ![]() получаем
получаем
![]()
т.е. ![]() . Обратно, если
. Обратно, если ![]() , то
, то ![]() . Теперь
. Теперь ![]() и
и ![]() – силовские подгруппы в
– силовские подгруппы в ![]() , которые по следствию 1.4 сопряжены в
, которые по следствию 1.4 сопряжены в ![]() , т.е. существует элемент
, т.е. существует элемент ![]() , такой, что
, такой, что ![]() . Теперь
. Теперь ![]() и
и ![]() , т.е.
, т.е.
![]()
Если
![]()
то ![]() и
и
![]()
Если ![]() , то пусть
, то пусть ![]() означает наивысшую степень
означает наивысшую степень ![]() , делящую порядок
, делящую порядок ![]() . По следствию 1.4
. По следствию 1.4 ![]() – порядок силовской
– порядок силовской ![]() –подгруппы из
–подгруппы из ![]() . Из следует, что
. Из следует, что
![]()
и
![]()
Если
![]()
то
![]()
и
![]()
Обратно, пусть
![]()
где ![]() ,
, ![]() и
и ![]() . Тогда
. Тогда
![]()
Поскольку уже доказано, что
![]()
то ![]() , где
, где
![]()
Теперь
![]()
и
![]()
Следовательно,
![]()
Пусть
![]()
Тогда ![]() делит
делит ![]() для каждого
для каждого ![]() и поэтому
и поэтому
![]()
делит ![]() , т.е.
, т.е. ![]() . Для
. Для ![]() имеем
имеем ![]() , откуда
, откуда ![]() .
.
Теорема доказана.
Лемма 1.6 Ошибка!. Если ![]() – нормальная подгруппа конечной группы
– нормальная подгруппа конечной группы ![]() и
и ![]() – силовская
– силовская ![]() – подгруппа из
– подгруппа из ![]() , то
, то ![]() .
.
Доказательство. Пусть ![]() – произвольный элемент из
– произвольный элемент из ![]() . Так как
. Так как ![]() , то
, то ![]() и по следствию 1.4 подгруппы
и по следствию 1.4 подгруппы ![]() и
и ![]() сопряжены в
сопряжены в ![]() . Поэтому, существует элемент
. Поэтому, существует элемент ![]() такой, что
такой, что ![]() , откуда
, откуда
![]()
и
![]()
Таким образом, ![]() .
.
Лемма доказана.
Лемма 1.7 Каждая подгруппа конечной группы, содержащая нормализатор некоторой силовской подгруппы, самонормализуема.
Доказательство. Пусть ![]() – силовская подгруппа группы
– силовская подгруппа группы ![]() и
и ![]() – подгруппа группы
– подгруппа группы ![]() , содержащая
, содержащая ![]() . Так как
. Так как ![]() , то по лемме Фраттини
, то по лемме Фраттини
![]()
Лемма доказана.
Лемма 1.8 Пусть ![]() –
– ![]() –подгруппа конечной группы
–подгруппа конечной группы ![]() ,
, ![]() и
и ![]() не делит
не делит ![]() . Тогда
. Тогда
![]()
Доказательство. Ясно, что
![]()
По условию подгруппа ![]() является силовской подгруппой в
является силовской подгруппой в ![]() . Пусть
. Пусть
![]()
Тогда ![]() и по лемме Фраттини
и по лемме Фраттини ![]() .
.
Лемма доказана.
Пример 1.9 Симметрическая группа ![]() степени 6 имеет порядок
степени 6 имеет порядок ![]() . По теореме Силова
. По теореме Силова ![]() содержит подгруппы порядков
содержит подгруппы порядков ![]() . Силовская 2‑подгруппа имеет порядок
. Силовская 2‑подгруппа имеет порядок ![]() , силовская 3‑подгруппа имеет порядок
, силовская 3‑подгруппа имеет порядок ![]() и силовская 5‑подгруппа имеет порядок 5.
и силовская 5‑подгруппа имеет порядок 5.
Пример 1.10 Группа порядка 15 циклическая.
Пусть ![]() – группа порядка 15. В группе
– группа порядка 15. В группе ![]() имеется подгруппа
имеется подгруппа ![]() порядка 3 и подгруппа
порядка 3 и подгруппа ![]() порядка 5. По следствию 1.4 число силовских 3‑подгрупп имеет вид
порядка 5. По следствию 1.4 число силовских 3‑подгрупп имеет вид ![]() для некоторого неотрицательного целого
для некоторого неотрицательного целого ![]() и делит 5. Поэтому в группе имеется только одна подгруппа порядка 3. Так как любые две силовские 3‑подгруппы сопряжены, то
и делит 5. Поэтому в группе имеется только одна подгруппа порядка 3. Так как любые две силовские 3‑подгруппы сопряжены, то ![]() . Аналогично, число силовских 5‑подгрупп равно
. Аналогично, число силовских 5‑подгрупп равно ![]() и делит 3. Поэтому
и делит 3. Поэтому ![]() . Так как
. Так как ![]() и
и ![]() – циклические подгруппы простых порядков, то группа
– циклические подгруппы простых порядков, то группа ![]() . Теперь для любых
. Теперь для любых ![]() имеем:
имеем:
![]()
![]()
поэтому
![]()
и ![]() . Следовательно, группа
. Следовательно, группа ![]() абелева. Теперь ясно, что
абелева. Теперь ясно, что ![]() – циклическая группа.
– циклическая группа.
Похожие работы
... такой параллелизм устраняется на основе введенного выше понятия слабой квазинормальности. Таким образом, задача изучения групп с заданной системой слабо квазинормальных подгрупп вполне актуальна, ее реализации посвящена данная работа. 1. Определение и общие свойства слабо нормальных подгрупп Определение. Подгруппа группы называется слабо нормальной в подгруппой, если существует такая ...
... как следствие первичных дефектов, и проблемах социальной адаптации аномальных людей к обществу здоровых. Проблема «норма—аномальность» далеко выходит за пределы медицины и является одной из актуальных проблем человекознания. Мы рассмотрели лишь некоторые подходы к ее решению. Психология развития представлена многочисленными теориями, акцентирующими внимание на различных сторонах этого феномена. ...
0 комментариев