Навигация
Взяв на плоскости прямоугольную декартову систему координат, изобразить области, определяемые следующими системами неравенств
4. Взяв на плоскости прямоугольную декартову систему координат, изобразить области, определяемые следующими системами неравенств.
а) 
Построим множество точек, определяемых 1-м, 2-м, 3-м неравенством.
Найдём пересечение этих множеств.
I. Построим эллипс ![]() но т. к. неравенство строгое, то точки эллипса не принадлежат искомой области, т.е. неравенство (2) задаёт внутренние точки эллипса.
но т. к. неравенство строгое, то точки эллипса не принадлежат искомой области, т.е. неравенство (2) задаёт внутренние точки эллипса.

Устанавливаем, что R = 3, 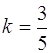 (0< k <1),
(0< k <1),  Cтроим осевой прямоугольник со сторонами
Cтроим осевой прямоугольник со сторонами  и изображаем эллипс.
и изображаем эллипс.
II. Строим множество точек, заданных вторым неравенством. Для этого строим прямую  и штрихуем определяемую область.
и штрихуем определяемую область.
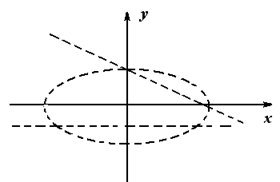
III. Аналогичные рассуждения для построения области, заданной неравенством у + 2 > 0.
Построение.
б) 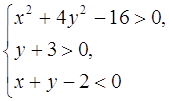
Построим множество точек, определяемых 1-м, 2-м, и 3-м неравенствами.
Найдём пересечение этих множеств.
I. ![]() – эллипс, точки которого не принадлежат искомой области (неравенство строгое), т.е. неравенство задаёт внешние точки эллипса. Приведём уравнение к каноническому виду
– эллипс, точки которого не принадлежат искомой области (неравенство строгое), т.е. неравенство задаёт внешние точки эллипса. Приведём уравнение к каноническому виду

Строим осевой прямоугольник со сторонами a и b, изображаем эллипс.
II. Строим множество точек, заданных неравенством (2). Для этого изображаем прямую у = 3 и штрихуем определяемую область.

III. Рассуждаем аналогично.
Построение.
Занятие №4–5Тема: Гипербола
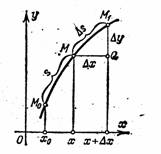
Учащиеся хорошо знакомы с гиперболой как с графиком функции  и с такими понятиями, как её ветви и асимптоты. Гипербола не только является центрально-симметричной линией (как график нечётной функции), но и имеет две оси симметрии – это биссектрисы пар вертикальных координатных углов (рис. 19).
и с такими понятиями, как её ветви и асимптоты. Гипербола не только является центрально-симметричной линией (как график нечётной функции), но и имеет две оси симметрии – это биссектрисы пар вертикальных координатных углов (рис. 19).
Рассмотрим уравнение x2 – y2 = l и покажем, что линия, задаваемая им – это тоже гипербола. Перепишем уравнение в виде (x – y) (x + y) = l. Введём новые переменные:  тогда в системе (u, v) исходное уравнение примет вид uv = l, и это будет гипербола, расположение ветвей которой полностью определяется знаком числа l.
тогда в системе (u, v) исходное уравнение примет вид uv = l, и это будет гипербола, расположение ветвей которой полностью определяется знаком числа l.
Для изображения гиперболы выясним, как расположены оси системы координат (u, v) в координатной плоскости (х, у), считая, что u – абсцисса и v – ордината в новой системе координат. Ось абсцисс – это множество точек, для которых v = 0, т.е. ![]() в исходной системе координат, или в исходной системе координат, или
в исходной системе координат, или в исходной системе координат, или ![]() . Это биссектриса чётных координат углов. Аналогично,
. Это биссектриса чётных координат углов. Аналогично, ![]() . Это биссектриса нечётных координатных углов. Для выяснения направлений на осях рассмотрим на оси Ou точку А (рис. 20), которая в системе координат (х, у) имеет координаты (1, -1). Тогда для этой точки u = 1 – (– 1) = 2 > 0, т.е. она лежит на положительной полуоси Оu. Аналогично, рассматривая на оси Ov точку В (1; – 1), получим, что для неё
. Это биссектриса нечётных координатных углов. Для выяснения направлений на осях рассмотрим на оси Ou точку А (рис. 20), которая в системе координат (х, у) имеет координаты (1, -1). Тогда для этой точки u = 1 – (– 1) = 2 > 0, т.е. она лежит на положительной полуоси Оu. Аналогично, рассматривая на оси Ov точку В (1; – 1), получим, что для неё ![]() , и, значит, она расположена на положительной полуоси Ov.
, и, значит, она расположена на положительной полуоси Ov.
Это позволяет сделать вывод о том, что преобразование  переводит систему координат (х, у) в систему (u, v), оси которой повёрнуты пол отношению к исходной на угол
переводит систему координат (х, у) в систему (u, v), оси которой повёрнуты пол отношению к исходной на угол ![]() .
.

Рис. 19

Рис. 20


Рис. 21
Уравнение при этом преобразуется в уравнение uv = l, которое равносильно уравнению  ибо
ибо ![]() равенство означало бы
равенство означало бы ![]() , и, значит,
, и, значит, ![]() В зависимости от знака числа l мы можем изобразить ветви гиперболы в соответствующих координатных четвертях системы
В зависимости от знака числа l мы можем изобразить ветви гиперболы в соответствующих координатных четвертях системы ![]() , тем самым будет получено изображение гиперболы, задаваемой уравнением
, тем самым будет получено изображение гиперболы, задаваемой уравнением ![]() в системе координат
в системе координат ![]() .
.
При этом, подставляя в исходное уравнение ![]() или
или ![]() в зависимости от знака l, мы получим точки пересечения гиперболы с той или иной координатной осью. Эти точки называются вершинами гиперболы (рис. 21).
в зависимости от знака l, мы получим точки пересечения гиперболы с той или иной координатной осью. Эти точки называются вершинами гиперболы (рис. 21).
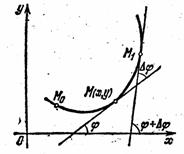
Если к гиперболе ![]() провести касательные в её вершинах (Теорема. Касательная к гиперболе в произвольной её точке является биссектрисой внутреннего угла М0 треугольника F1M0F2, имеющего своими вершинами фокусы гиперболы и данную точку М0, см. рис. 27), то они пересекут асимптоты гиперболы в точках, которые будут вершинами квадрата (это следует из соображений симметрии). Удобно этот квадрат назвать осевым квадратом гиперболы (рис. 23). Центр этого квадрата совпадает с центром симметрии гиперболы, её диагонали – это её асимптоты, а сторона равна
провести касательные в её вершинах (Теорема. Касательная к гиперболе в произвольной её точке является биссектрисой внутреннего угла М0 треугольника F1M0F2, имеющего своими вершинами фокусы гиперболы и данную точку М0, см. рис. 27), то они пересекут асимптоты гиперболы в точках, которые будут вершинами квадрата (это следует из соображений симметрии). Удобно этот квадрат назвать осевым квадратом гиперболы (рис. 23). Центр этого квадрата совпадает с центром симметрии гиперболы, её диагонали – это её асимптоты, а сторона равна ![]() .
.

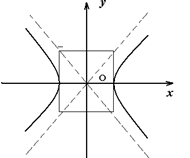
Рис. 22, 23
Если произвести сжатие к оси Ох с коэффициентом k > 0, k ¹ 1, то гипербола преобразуется в линию, также называемую гиперболой, но о такой гиперболе говорят, что она неравнобокая. Исходную же гиперболу называют равнобокой. Прн сжатии осевой квадрат преобразуется в осевой прямоугольник, а диагонали квадрата – в диагонали прямоугольника (они будут асимптотами для получающейся неравнобокой гиперболы). Уравнение неравнобокой гиперболы имеет вид: ![]() , где k2 ¹ 1.
, где k2 ¹ 1.
 Рис. 24
Рис. 24
Таким образом, уравнение ![]() (k ¹ 0, l ¹ 0) всегда задаёт гиперболу. Она равнобокая, если k = 1 и неравнобокая, если k = -1. Её вершины лежат на оси Ох, если l > 0, и на оси Оу, если l < 0. Для её изображения нужно сначала построить осевой прямоугольник, его диагонали и вершины гиперболы (рис. 24).
(k ¹ 0, l ¹ 0) всегда задаёт гиперболу. Она равнобокая, если k = 1 и неравнобокая, если k = -1. Её вершины лежат на оси Ох, если l > 0, и на оси Оу, если l < 0. Для её изображения нужно сначала построить осевой прямоугольник, его диагонали и вершины гиперболы (рис. 24).
Преобразуем уравнение ![]() . Разделим обе его части на l:
. Разделим обе его части на l:

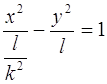 (1)
(1)
Если l > 0, то уравнение примет вид (1), а если
l < 0 – 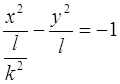 (2).
(2).
Сделаем замену  ,
, ![]() , тогда получим уравнение гиперболы в общем виде
, тогда получим уравнение гиперболы в общем виде
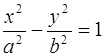 (3)
(3)  (4).
(4).
Уравнения (3) и (4) называются каноническими уравнениями, а гиперболы, заданные этими уравнениями, называются сопряжёнными, а и b – стороны осевого прямоугольника. Если a = b – осевого квадрата.
Для закрепления решим несколько задач. [17]
1) Построить графики.
а) ![]()
I способ.
Это уравнение равносильно уравнению 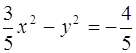 . Поскольку l < 0, то вершины гиперболы расположены на оси Оу. Гипербола неравнобокая, т. к.
. Поскольку l < 0, то вершины гиперболы расположены на оси Оу. Гипербола неравнобокая, т. к.  . Строим осевой прямоугольник со сторонами
. Строим осевой прямоугольник со сторонами ![]() и
и ![]() , где
, где  ,
,  . Чертим график гиперболы.
. Чертим график гиперболы.
II. способ
Приведём уравнение к каноническому виду
![]() ,
,  , следовательно,
, следовательно, 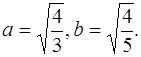 Строим осевой прямоугольник, а затем изображаем гиперболу.
Строим осевой прямоугольник, а затем изображаем гиперболу.
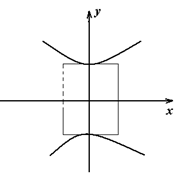
Параллельный перенос гиперболы преобразует уравнение к виду:
![]() (5) (или
(5) (или 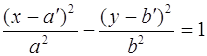 (6)).
(6)).
Рассмотрим способ построения гиперболы по уравнению данного вида.
б) ![]() . Преобразуем его к виду (5)
. Преобразуем его к виду (5) ![]() и далее:
и далее:  Это уравнение гиперболы, где
Это уравнение гиперболы, где 
 Осевой прямоугольник со сторонами
Осевой прямоугольник со сторонами  смещён на две единицы вверх и вправо. Строим его и изображаем гиперболу.
смещён на две единицы вверх и вправо. Строим его и изображаем гиперболу.

II способ.
Приводим уравнение к каноническому виду:
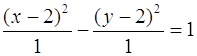 , следовательно,
, следовательно, 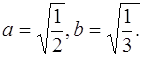
Центр осевого прямоугольника – точка (2; 2).
Строим его и изображаем гиперболу.
2) Найти длины полуосей и координаты фокусов следующих гипербол:
а) ![]()
![]()
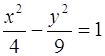 .
.
Привели к каноническому виду, а следовательно а = 2, b = 3.
F1 и F2 имеют координаты: F1(– с; 0), F2(с; 0).
![]()
Таким образом, F1(![]() ; 0), F1(
; 0), F1(![]() ; 0).
; 0).
Ответ: а = 2, b = 3, F1(![]() ; 0), F1(
; 0), F1(![]() ; 0).
; 0).
б) ![]()
![]()
 Используя каноническое уравнение, получим:
Используя каноническое уравнение, получим:
![]() .
.
Мы знаем, что F1(– с; 0), F2(с; 0),
![]()
Итак, ![]() , F1(
, F1(![]() ; 0), F1(
; 0), F1(![]() ; 0).
; 0).
в) ![]()
![]() ,
, 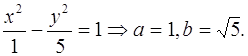
F1(– с; 0), F2(с; 0): ![]()
Ответ: ![]() F1(
F1(![]() ; 0), F1(
; 0), F1(![]() ; 0).
; 0).
3) Составить каноническое уравнение гиперболы, если расстояние между вершинами равно 8, а расстояние между фокусами равно 10;
Итак, нам дано, что ![]() Находим, что
Находим, что ![]() .
.
Каноническое уравнение гиперболы имеет вид  Т. к.
Т. к. ![]() , то уравнение можно записать следующим образом:
, то уравнение можно записать следующим образом: 
4) Взяв на плоскости прямоугольную декартову систему координат, построить области, определяемые следующими системами неравенств:
а) 
построим множество точек, определяемых 1-м и 2-м неравенствами. Найдём пересечение этих множеств.
I. Построим гиперболу ![]() . После преобразования получаем каноническое уравнение
. После преобразования получаем каноническое уравнение  с полуосями а = 2 и b = 1. Точки гиперболы не принадлежат искомой области, т. к. неравенство строгое. Это неравенство определяет внутренние точки гиперболы. Строим осевой прямоугольник, гиперболу и изображаем искомую область.
с полуосями а = 2 и b = 1. Точки гиперболы не принадлежат искомой области, т. к. неравенство строгое. Это неравенство определяет внутренние точки гиперболы. Строим осевой прямоугольник, гиперболу и изображаем искомую область.
II. Строим множество точек. Заданных вторым неравенством. Для этого изображаем прямую  и штрихуем определяемую область.
и штрихуем определяемую область.
Построение.
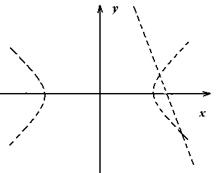
б) 
Построим множество точек, определяемых 1-м, 2-м. 3-м неравенствами. Найдём пересечение этих множеств.
I. построим гиперболу ![]() . Её точки принадлежат искомой области, т. к. неравенство не строгое. Т. о. Неравенство определяет внешние точки гиперболы. Преобразуем уравнение.
. Её точки принадлежат искомой области, т. к. неравенство не строгое. Т. о. Неравенство определяет внешние точки гиперболы. Преобразуем уравнение.  это уравнение гиперболы, где
это уравнение гиперболы, где  , точки которой не принадлежат искомой области (неравенство строгое),
, точки которой не принадлежат искомой области (неравенство строгое),  строим осевой прямоугольник со сторонами
строим осевой прямоугольник со сторонами  и изображаем гиперболу.
и изображаем гиперболу.
II. Строим множество точек, заданных вторым неравенством. Для этого изображаем прямую ![]() и штрихуем определяемую область.
и штрихуем определяемую область.
III. Рассуждаем аналогично. строим прямую ![]() и штрихуем определяемую область.
и штрихуем определяемую область.
Построение.

Некоторые практические материалы. Предложенные в гл. II проверены экспериментально в 10–11 классах ГОУ СОШ с. Новкус-Артезиан.
Тема эксперимента: «Различные уравнения эллипса, гиперболы, параболы и их графики».
Эксперимент проводился в два этапа.
I этап эксперимента.
До изложения теории о линиях второго порядка (до Темы 1) предлагались задания на проверку уровня знаний учащихся о знакомых им линиях второго порядка.
Учащимся было предложено ответить на вопросы и выполнить задания:
1. Какие из перечисленных ниже графиков представлены на чертеже:
а) окружность;
б) эллипс;
в) гипербола;
г) парабола?


2. Каким из перечисленных выше уравнений задаётся каждый из них:
а)  ,
,
б) ![]()
в) ![]()
г) 
3. Какие методы построения графиков функции вы знаете?
4. Приведите примеры распространения линий второго порядка в жизни, природе, технике.
5. Какие вы знаете свойства эллипса, гиперболы, параболы, окружности?
II этап поискового эксперимента проводился после проведения факультативных занятий.
Подбирались задачи, аналогичные тем, которые рассматривались на кружковых занятиях. Задания достаточно стандартные, аналогичные тем, которые были проведены на первом этапе эксперимента и задания по нестандартному решению задач.
Учащимся были предложены следующие задания:
1. Нарисовать схематически графики данных уравнений:
а) 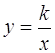 ,
,
б) ![]()
в) ![]()
г) 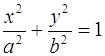 .
.
2. По заданным уравнениям определите название линии второго порядка:
а) ![]()
б) ![]()
в) ![]()
г) ![]() .
.
3. Построить график функции ![]()
4. Решить уравнения: а) ![]()
б) ![]()
После проведения эксперимента можно сделать следующий вывод: у учащихся экспериментальной группы значительно поднимается уровень логического мышления и развивается математическая интуиция, они чётко аргументируют ответы, приводят доказательства и хорошо ориентируются в изученном материале, применяя его на уроках.
Результаты эксперимента
| Количество учащихся | I этап | II этап |
| 15 | 28% | 75% |
Заключение
В квалификационной работе разработана теория плоских кривых и замечательных кривых, предложена разработка факультатива для учащихся 9–11 классов на тему «Плоские кривые».
После изучения научной и методической литературы материал отобран с учётом психологических и физиологических особенностей учащихся старших классов и систематизирован для целостного изложения.
Выдвинутая гипотеза, на наш взгляд подтверждается на основе наблюдений и частичного эксперимента в период педагогической практики.
Содержание всех занятий позволяет углубить представление учащихся об эллипсе, гиперболе. Параболе и ознакомить их с некоторыми, наиболее часто встречающимися замечательными кривыми, приблизить их к пониманию некоторых важных идей современной математики.
Литература
1. Савелов А.А. Плоские кривые. – М.: ГИФ-МЛ, 1960
2. Гильберт Д., Кон-Фостен С. Наглядная геометрия. – М.: Наука, 1981.
3. Моденов П.С. Аналитическая геометрия М.: Наука, 1969
4. Атанасян Л.С., Базылев В.Т. Геометрия. – учебное пособие для студентов физ. – мат. факультетов пед. институтов. – М.: Просвещение, 1987
5. Александров П.С. Лекции по аналитической геометрии, пополненные необходимыми сведениями из алгебры с приложениями собрания задач, снабжённых решениями, составленные А.С. Пархоменко. – М.: Наука, 1968
6. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1979
7. Энциклопедический словарь юного математика. М.: Педагогика, 1989
8. Математический энциклопедический словарь. М.: Советская энциклопедия, 1988
9. Маркушевич А.И. Замечательные кривые. – М.: – наука, 1978
10. Водинчар М.И., Лайкова Г.А., Калинова Т.Ю. Линии второго порядка и графики иррациональных функций // Математика в школе, 1999, №3.
11. Дубровин В.А., Новиков С.П., Фоменко А.Г. Современная геометрия. Методы и приложения. – М. Наука, 1986
12. Методика преподавания математики в средней школе. – М.: Просвещение, 1980
13. Кузнецова Г.Б. Алгебра точек параболы // Математика в школе, 1974, №2
14. Ткаченко А.А. Об одном свойстве гиперболы // Математика в школе, 1976, №2
15. Лабораторные и практические работы по методике преподавания математики: учебное пособие для физ. – мат. Специальностей пед. институтов \ под редакцией Лященко Е.И. – М., 1988
16. Шарыгин И.Ф. Факультативный курс по математике: решение задач. Уч. пособие для 10 кл. средней школы. – М., 1989
17. Абрамов А.Щ., Ивлев Б.М. и др. Задачи повышенной трудности по алгебре и началам анализа: уч. пособие для 10–11 кл. средней школы. – М., 1993
18. Программа общеобразовательных учреждений. Математика. – М. «Просвещение», 2002
Похожие работы
... можно показать, что формулы будут справедливы и в случае y!!<0. Параметрическое задание кривой Если кривая задана параметрически: x = j(t), y = y(t), то координаты центра кривизны можно получить из формул *, подставляя в них вместо y! и y!! их выражения через параметр: . Тогда (2) Эволюта и эвольвента Если в точке M1(x, y) данной линии кривизна отлична от нуля, то этой точке соответствует ...
... і координат , Матимемо (10.12) Пропонується вивести цю формулу, узявши до уваги, що рівняння кривої в полярних координатах можна записати як параметричні з параметром q : і використавши формулу (10.10). Приклад 1. Обчислити довжину кривої, заданої рівнянням Розв‘язок. Досить обчислити довжину дуги, що обмежує зверху заштриховану на рис.10.7 фігуру, а потім помножити її на ...
... дуги. Спиралями являются также эвольвенты замкнутых кривых, например эвольвента окружности. Названия некоторым спиралям даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например: · параболическая спираль (а - r)2 = bj, · гиперболическая спираль: r = а/j. · Жезл: r2 = a/j · si-ci-cпираль, параметрические уравнения которой имеют вид: , [si (t) и ci ...
... закону. Эту линию называют образующей. Она может быть прямой, и тогда образованную ею поверхность относят к классу линейчатых. Если образующая - кривая линия, поверхность считают нелинейчатой. Линию, по которой перемещают образующую, называют направляющей. В качестве последней иногда используют след поверхности, т. е. линию ее пересечения с плоскостью проекций. Определителем поверхности называют ...
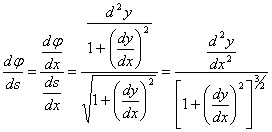



0 комментариев