Навигация
Точка О (0; 0) принадлежит эллипсу;
1. Точка О (0; 0) принадлежит эллипсу;
2. х и у входят в уравнение чётной системы, поэтому если точка М (х; у) принадлежит эллипсу, то эллипсу принадлежит точка М1(-х; у), М2(х; – у), М3(-х; – у), следовательно, эллипс – фигура, симметричная относительно Ох, Оу, начала координат. Оси Ох, Оу, являются осями симметрии эллипса. Можно доказать, что эллипс, отличный от окружности, не имеет других осей симметрии;
3. Найдём точки пересечения с осями координат:
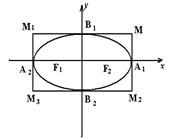
Рис. 13
С осью Ох: у=0 
![]() А1(а; 0), А2(-а; 0)
А1(а; 0), А2(-а; 0)
С осью Оу: х=0, 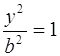
![]() В1(b; 0), B2(-b; 0)
В1(b; 0), B2(-b; 0)
a >b, т. к. b2 = a2 – b2, следовательно А1A2 – большая ось эллипса, В1В2 – малая ось эллипса;
Исследуем поведение эллипса в первой четверти:
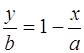
 , следовательно,
, следовательно, ![]() .
.
Так, с возрастанием х от 0 до а у < b, то функция у в первой четверти убывающая. При х = 0, у = b; при х = а у = 0, А1A2 – вершины эллипса.
Гиперболой называется геометрическое место точек, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное положительное число 2а, меньшее, чем расстояние 2с между фокусами. [5]
Каноническим уравнением гиперболы является уравнение 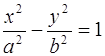 . Оно используется для изучения её геометрических свойств (см. рис. 14):
. Оно используется для изучения её геометрических свойств (см. рис. 14):
1. Точка О (0; 0) не принадлежит гиперболе.
2. Гипербола симметрична относительно осей и начала координат. Так же как и в случае эллипса, точка О является центром симметрии гиперболы, а прямые Ох и Оу – осями симметрии. Центр симметрии называется центром гиперболы.
3. С осью Ох: у=0 
![]() , А1(а; 0), А2(-а; 0)
, А1(а; 0), А2(-а; 0)
С осью Оу: х=0, 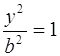
![]() , В1(b; 0), B2(-b; 0)
, В1(b; 0), B2(-b; 0)
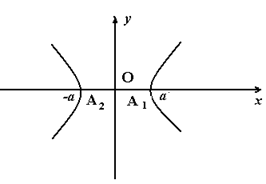
Рис. 14
4. Т. о. 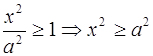
![]() х = – а и х = а – точки гиперболы лежат вне полосы. [14]
х = – а и х = а – точки гиперболы лежат вне полосы. [14]
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, не проходящей через фокус, и называемой директриссой. [7, 8]
Расстояние от фокуса параболы до её директрисы называется параметром параболы. Эксцентриситет параболы принимается равным единице.
Уравнение у = 2 рх является каноническим уравнением параболы. Каноническое уравнение параболы также используется для изучения её геометрических свойств (см. рис. 15):

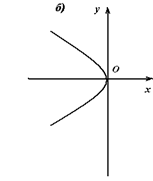
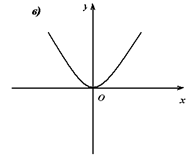
Рис. 15
1. Точка О (0; 0) принадлежит гиперболе;
2. Если точка М (х; у) принадлежит параболе, то точка М1(х; – у) также принадлежит параболе, следовательно, парабола симметрична относительно Оу.
3. Из уравнения параболы у – любое, ![]() , т.е. «ветви» параболы расположатся в положительной полуплоскости, относительно Оу.
, т.е. «ветви» параболы расположатся в положительной полуплоскости, относительно Оу.
4. В I четверти ![]() , при
, при ![]() ,
, ![]() . В первой четверти у возрастает. [13]
. В первой четверти у возрастает. [13]
5. Цели и задачи факультативных занятий
В настоящее время традиционный взгляд на содержание обучения математике, её роль и место в общем образовании пересматривается и уточняется. Для продуктивной деятельности в современном мире требуется достаточно прочная базовая математическая подготовка.
Факультативные занятия по математике призваны углублять математические знания школьников, уже определивших основной круг своих учебных интересов.
Главной целью факультативных занятий по математике является углубление и расширение знаний, развитие интереса учащихся к предмету, развитие их математических способностей, привитие школьникам интереса и вкуса к самостоятельным занятиям математикой, воспитание инициативы и творчества.
Для того, чтобы факультативные занятия по математике были эффективными, необходимо организовать там, где есть:
1) высококвалифицированные учителя или другие специалисты, способные вести занятия на высоком научно – методическом уровне;
2) не менее 15 учащихся, желающих изучать данный факультативный курс. [12]
Факультативы – занятия, основанные на принципе добровольного участия и призванные решать три основные задачи:
1) повышение уровня математического мышления, углубление теоретических знаний и развитие практических навыков учащихся, выявления математических способностей;
2) организация досуга учащихся в свободное от учёбы время.
Данный факультатив предназначен для учеников 11 классов.
Для проведения факультатива выделяется 1 час в неделю, всего 16 часов, разработан на первое полугодие. [18]
По существу, факультативные занятия являются наиболее динамичной разновидностью дифференциации обучения.
6. Тематическое планирование факультатива| 1 | История изучения плоских кривых | 1 ч |
| 2 | Способы образования кривых | 3 ч |
|
| Классификация плоских кривых | 4 ч |
| 3 | Алгебраические кривые | 1 ч |
| 4 | Род алгебраических кривых | 2 ч |
| 5 | Трансцендентные кривые | 1 ч |
|
| Кривые, изучаемые в школьном курсе математики | 6 ч |
| 6 | Эллипс | 1 ч |
| 7 | Гипербола | 1 ч |
| 8 | Парабола | 2 ч |
| 9 | Итоговое занятие. Выпуск математической газеты | 2 ч |
Тема: История изучения плоских кривых
Цели: 1) познакомить с историей изучения плоских кривых;
2) развить интерес у учащихся к знаниям, повысить интерес к учению;
3) углубить знания, полученные на уроках математики.
Ход занятия
I. Организационный момент
II. Основная часть
1) Лекция об истории изучения плоских кривых [см. гл. I § 1]
2) Задание
Ребята, разгадаем с вами кроссворд:
ПАСКАЛЬ
ПАПИРУС
АПОЛЛОНИЙ
РОБЕРВАЛЬ
АРХИМЕД
ГЕОМЕТРИЯ
По горизонтали
1. Учёный, считавший, что дуга спирали Архимеда равна дуге параболы
2. Египтяне за 17–20 веков до нашей эры занимались квадратурой круга. Как назывался документ?
3. Кто написал трактат о конических сечениях? (3–2 в. до н.э.)
4. Какой учёный показал, что задача спрямления спирали идентична задаче спрямления параболы?
5. Учёный, решивший задачу о квадратуре сегмента параболы.
6. Как называлась книга Р. Декарта, изданная в 1637 году?
По вертикали
1. Название линии, прошедшей большой исторический период.
III. Итог занятия
1) Домашнее задание
Написать реферат на тему «История изучения плоских кривых».
Занятие №2–3Тема: Эллипс
В декартовой системе координат, как хорошо известно, окружность радиуса R c центром C (a; b) задаётся уравнением (x2 – a2) + (y2 – b2) = R2. Если сжать окружность с центром в начале координат к вертикальному диаметру с коэффициентом k > 0, то получится линия с уравнением k2x2 + y2 = R2 (1), которая называется эллипсом. При этом ясно, что если k > 1, то это действительно сжатие в привычном смысле этого слова (рис. 16, а), а если 0 < k < 1, то это растяжение (рис. 16, б). Но договоримся использовать один общий термин – сжатие.
Преобразуем уравнение (1). Разделим его обе части на R2:
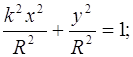

 всегда.
всегда.
Сделаем замену  и
и ![]() , тогда получим уравнение эллипса в общем виде;
, тогда получим уравнение эллипса в общем виде;  (2).
(2).

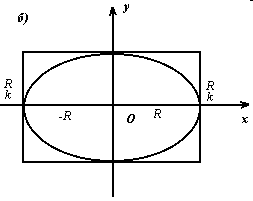
Рис. 16
Уравнение (2) называется каноническим уравнением эллипса. В школьном курсе изучается уравнение окружности с центром в начале координат ![]() (3).
(3).
Посмотрим, как связаны окружность и эллипс.
В уравнении (3) сделаем замену 
![]() Разделим на R2:
Разделим на R2:
 . Пусть
. Пусть  , тогда
, тогда  .
.
Итак, мы видим, что окружность – частный случай эллипса, когда а = b.
Отметим ещё, возвращаясь к уравнению (1), что окружность – это эллипс, где k = 1.
Из уравнений видно, что эллипс – линия, симметричная относительно обеих осей координат, а значит, и центрально-симметричная. Геометрически, он полностью характеризуется одним из поперечных размеров (они называются осями эллипса) и их отношением.
Вокруг эллипса естественным образом описывается прямоугольник со сторонами, равными осям эллипса и параллельными координатным прямым, который является результатом сжатия квадрата, описанного вокруг исходной окружности. Называется он осевым прямоугольником эллипса. Если научиться его строить по уравнению эллипса, то довольно легко после этого изобразить и сам эллипс.
1) Например, дано уравнение а) 3х2 + у2 = 7. Изобразить эллипс двумя способами. [16]
I способ
Запишем его в виде ![]() . Устанавливаем, что
. Устанавливаем, что ![]() , строим осевой прямоугольник со сторонами 2R, l и изображаем сам эллипс (рис. 17). Отметим, что в правой части уравнения должно быть положительное число, а в левой – сумма квадрата абсциссы, взятого с положительным коэффициентом, и квадрата ординаты.
, строим осевой прямоугольник со сторонами 2R, l и изображаем сам эллипс (рис. 17). Отметим, что в правой части уравнения должно быть положительное число, а в левой – сумма квадрата абсциссы, взятого с положительным коэффициентом, и квадрата ординаты.
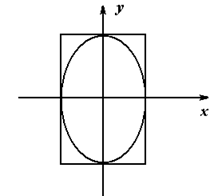
Рис. 17
II способ
Приведём уравнение к каноническому виду.
Разделим обе его части на 7.

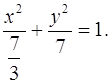
Получим, что 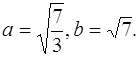
Строим осевой прямоугольник со сторонами а и 2b, а затем изображаем эллипс.
Отметим, что, например, уравнение 3х2 + 5у2 = 7 следует сначала преобразовать к виду х2 + у2 = ![]() или
или 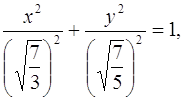 а затем находить R, k и a, b соответственно.
а затем находить R, k и a, b соответственно.
Если центр эллипса находится не в начале координат, но его оси параллельны координатным осям, то он задаётся уравнением ![]() (4),
(4),
где С (а; b) – центр эллипса. Это легко следует из формул параллельного переноса, или каноническим уравнением
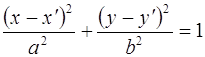 (5) – С (х; у) – центр эллипса.
(5) – С (х; у) – центр эллипса.
Данного материала достаточно для построения эллипса в том случае, если он задан уравнением, содержащем как квадраты, так и первые степени переменных.
б) ![]()
I способ
Преобразуем к виду (4): 
Это уравнение эллипса с центром в точке С (5; – 4), где k =  (рис. 18)
(рис. 18)

Рис. 18
II способ
Преобразуем к виду (5): 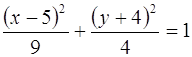 . Получили уравнение эллипса с центром в точке С (5; – 4), где а = 3, b = 2.
. Получили уравнение эллипса с центром в точке С (5; – 4), где а = 3, b = 2.
Строим сам эллипс.
2. Найти длины полуосей и координаты фокусов следующих эллипсов:
а) ![]()
Приводим уравнение к каноническому виду  , а = 3, b = 2.
, а = 3, b = 2.
Фокусы F1 и F2 имеют координаты F1(с; 0) и F2(– с; 0).
![]()
Итак, F1(![]() ; 0) и F2(
; 0) и F2(![]() ; 0) а = 3, b = 2.
; 0) а = 3, b = 2.
б) ![]() Решаем аналогично а).
Решаем аналогично а).  , а = 3, b = 1.
, а = 3, b = 1.
F1(с; 0), F2(– с; 0). ![]()
Итак, F1(![]() ; 0) и F2(
; 0) и F2(![]() ; 0) а = 3, b = 1.
; 0) а = 3, b = 1.
в) ![]()
 , а =
, а = ![]() , b =
, b = ![]() .
.
F1(с; 0), F2(– с; 0): 
Итак, а = ![]() , b =
, b = ![]() , F1(
, F1(![]() ; 0), F2(-
; 0), F2(-![]() ; 0).
; 0).
3. Найти координаты точек М, принадлежащих эллипсу 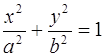 и равноудалённых от фокусов.
и равноудалённых от фокусов.
Пусть М (х; у), тогда МF1 = МF2 (по условию). Т. к. F1(с; 0), F2(– с; 0): ![]() то
то ![]()
![]()
Если х = 0, то, подставляя его в исходное уравнение, получим: 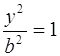 ,
, ![]() Следовательно,
Следовательно, ![]() и
и ![]() .
.
Похожие работы
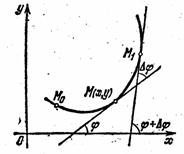
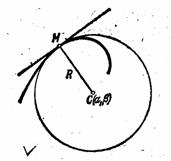
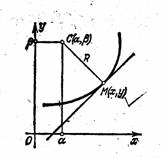
... можно показать, что формулы будут справедливы и в случае y!!<0. Параметрическое задание кривой Если кривая задана параметрически: x = j(t), y = y(t), то координаты центра кривизны можно получить из формул *, подставляя в них вместо y! и y!! их выражения через параметр: . Тогда (2) Эволюта и эвольвента Если в точке M1(x, y) данной линии кривизна отлична от нуля, то этой точке соответствует ...
... і координат , Матимемо (10.12) Пропонується вивести цю формулу, узявши до уваги, що рівняння кривої в полярних координатах можна записати як параметричні з параметром q : і використавши формулу (10.10). Приклад 1. Обчислити довжину кривої, заданої рівнянням Розв‘язок. Досить обчислити довжину дуги, що обмежує зверху заштриховану на рис.10.7 фігуру, а потім помножити її на ...
... дуги. Спиралями являются также эвольвенты замкнутых кривых, например эвольвента окружности. Названия некоторым спиралям даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например: · параболическая спираль (а - r)2 = bj, · гиперболическая спираль: r = а/j. · Жезл: r2 = a/j · si-ci-cпираль, параметрические уравнения которой имеют вид: , [si (t) и ci ...
... закону. Эту линию называют образующей. Она может быть прямой, и тогда образованную ею поверхность относят к классу линейчатых. Если образующая - кривая линия, поверхность считают нелинейчатой. Линию, по которой перемещают образующую, называют направляющей. В качестве последней иногда используют след поверхности, т. е. линию ее пересечения с плоскостью проекций. Определителем поверхности называют ...
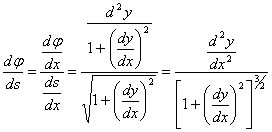



0 комментариев