Навигация
Оценка погрешности и сходимость методов Рунге-Кутты
39910
знаков
10
таблиц
20
изображений
1.7 Оценка погрешности и сходимость методов Рунге-Кутты
Со времен работы Лагранжа и особенно Коши всякий установленный численно результат принято сопровождать надежной оценкой погрешности. Лагранж дал известные оценки погрешности многочленов Тейлора, а Коши вывел оценки для погрешности метода ломаных Эйлера. Через несколько лет после первых успехов методов Рунге-Кутты также пришел к заключению, что для этих методов нужны оценки погрешностей[2].
1.7.1 Строгие оценки погрешности
Способ, которым Рунге получил оценку погрешности, делаемой на одном шаге («локальной погрешности»), может быть описан следующим образом. Для метода порядка 
рассмотрим локальную погрешность
(2.7.1)
и воспользуемся ее тейлоровским разложением:
, (2.7.2)
где 
и 
. Явное вычисление 
дает выражение вида
, (2.7.3)
где 
и 
содержат частные производные 
до порядков 
и соответственно. Далее поскольку 
, имеем 
. Таким образом, если ограничены все частные производные до порядка включительно, имеем 
и 
. Следовательно, существует постоянная 
такая, что 
и
. (2.7.4)
Бибербах использовал несколько иной подход. Запишем
(2.7.5)
и воспользуемся тейлоровскими разложениями
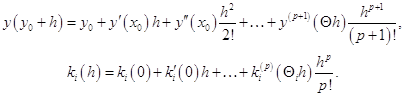(2.7.6)
Для векторных функций эти формулы справедливы покомпонентно (возможно, с различным 
). В силу условий порядка первые члены разложения (2.6.5) по степеням 
обращаются в нуль. Таким образом, справедлива следующая теорема.
Теорема.
Если метод Рунге-Кутты (2.3.1) имеет порядок и если все частные производные 
до порядка включительно существуют и непрерывны, то локальная погрешность метода (2.3.1) допускает следующую строгую оценку:
, (2.7.7)
или
. (2.7.8)
Продемонстрируем этот результат, применяя к скалярному дифференциальному уравнению первый метод Рунге-Кутты (2.2.4), который имеет порядок 
. Дифференцируя (2.1.1), получим
. (2.7.9)
Вторая производная величины 
имеет вид
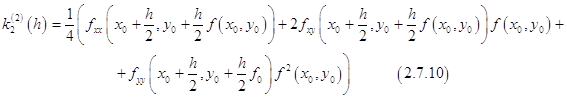
Если условия теоремы выполнены, то легко видеть, что выражения (2.7.9) и (2.7.10) ограничены постоянной, которая не зависит от , что и дает оценку (2.7.8).
Похожие работы
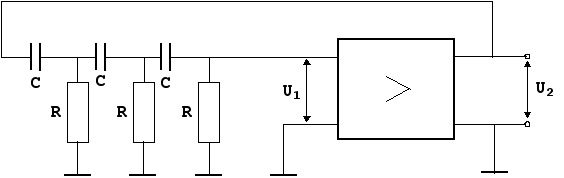
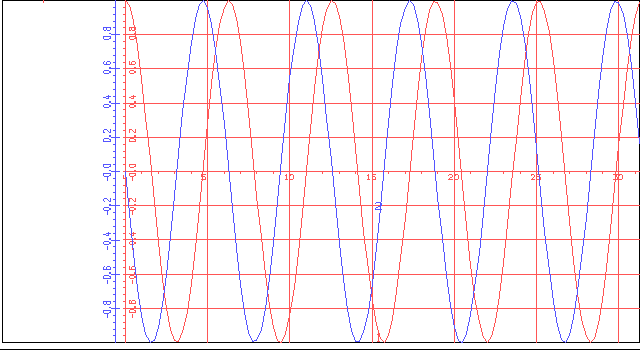
... 1 0.0001 Графики решения приведены на Рисунке 8, а численные значения в таблице 8. Рисунок показывает, что выходное напряжение автогенератора (кривая 1) достаточно близко к синусоидальному, чего нельзя сказать о входном напряжении усилителя (кривая 2). Таблица 8 АРГУМЕНТ ФУНКЦИЯ 1 ФУНКЦИЯ 2 ФУНКЦИЯ 3 ФУНКЦИЯ 4 ФУНКЦИЯ 5 370.0 ...
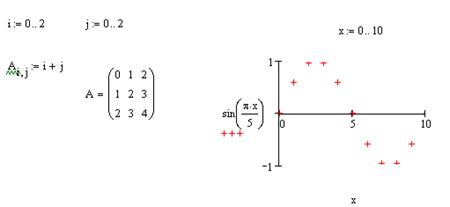
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...
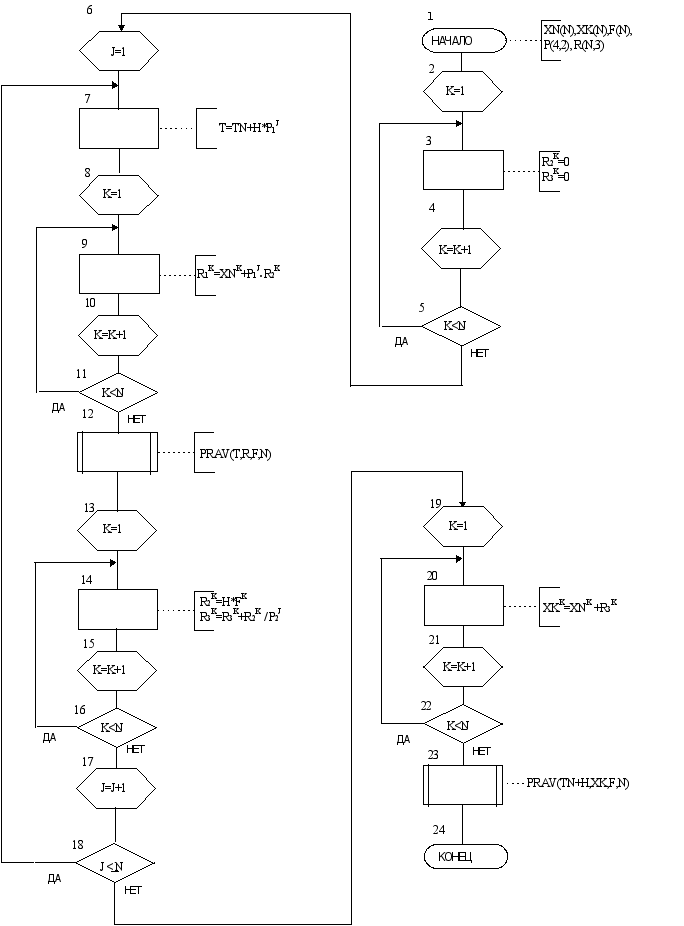
... методы (метод Гаусса). Однако, при решении на ЭВМ систем высокого порядка (более 200 уравнений в системе), предпочтительными являются итерационные методы. Реализация решения задачи анализа линейного стационарного объекта может быть осуществлена с помощью средств матричной алгебры пакета MathCAD. 1.2. Последовательность выполнения работы 1. Согласно номеру варианта (две последние цифры ...
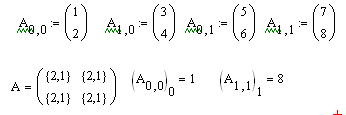
0 комментариев