Навигация
Условия порядков для методов Рунге-Кутты
39910
знаков
10
таблиц
20
изображений
1.6 Условия порядков для методов Рунге-Кутты
Рассмотрим структуру условий, определяющих порядок метода, или условий порядка, как их называют для краткости. Способ вывода условий порядка прошел большую эволюцию. Он совершенствовался главным образом под влиянием работ Бутчера.
Так как явные методы Рунге-Кутты являются частным случаем неявных, то можем выписать условия, при которых метод имеет заданный порядок.
Метод
|
|
|
|
|
(где на свободных местах должны стоять нули) имеет порядок 
, если удовлетворяется уравнение
(2.6.1)
для каждого дерева 
с корнем и не более чем с разветвлениями[1].
При 
эти условия, обеспечивающие порядок 4, и соответствующие деревья имеют следующий вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.6.2)
(2.6.3)
(2.6.4)
(2.6.5)
(2.6.6)
(2.6.7)
(2.6.8)
(2.6.9)Заметим, что для меньших значений мы берем соответствующее подмножество этих условий, а для меньших 
оставляем лишь некоторые из указанных членов.
Из (2.9) видим, что действительно необходимо 4 этапа, так как если бы их было меньше, то был бы опущен единственный член в левой части этого уравнения. Для явных методов в общем случае выполняется неравенство 
. Фактически (для тех значений, для которых это известно) минимальное значение для данного указано в следующей таблице:
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
| 1 | 2 | 3 | 4 | 6 | 7 | 9 |
Общие классы методов с этими значениями и легко найти в случае 
.
Для 
:
| 0 | |
| 1 |
Это известный метод Эйлера.
Для 
:
|
|
|
|
|
Это однопараметрическое семейство имеет требуемый порядок для любого ненулевого значения 
.
Для 
имеется три семейства, из которых первые два таковы:
|
|
|
|
| |
|
|
|
|
|
Каждое из них имеет один параметр 
. Третье семейство имеет в качестве параметров 
и 
, причем
.
Вывод методов с 
более сложен, но его можно упростить, положив
(2.6.10)
(что влечет равенство 
), так как это позволяет опустить уравнения (2.6.3), (2.6.5), (2.6.8) и (2.6.9). Интересно также, что (2.6.10) является следствием (2.6.2) – (2.6.9).
План вывода конкретного метода этого порядка можно выполнить при условии, что не возникает несовместных систем.
Шаг 1. Выбираем значения , и полагаем .
Шаг 2. Из (2.6.2), (2.6.3), (2.6.4) и (2.6.6) находим 
.
Шаг 3. Из уравнения 
(это уравнение есть разность уравнений (2.6.5) и (2.6.7)) находим 
.
Шаг 4. Из (2.6.10) находим 
.
Шаг 5. Вычисляем 
.
В случае 
шаг 2 приводит к выбору 
и 
при условии, что 
, 
. В частности, имеем известный метод:
|
|
|
|
Похожие работы
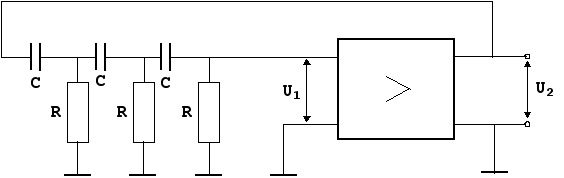
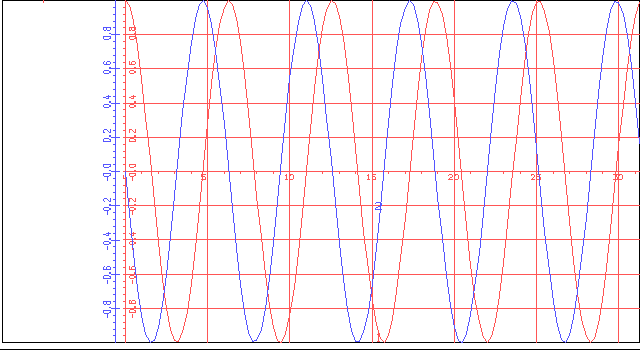
... 1 0.0001 Графики решения приведены на Рисунке 8, а численные значения в таблице 8. Рисунок показывает, что выходное напряжение автогенератора (кривая 1) достаточно близко к синусоидальному, чего нельзя сказать о входном напряжении усилителя (кривая 2). Таблица 8 АРГУМЕНТ ФУНКЦИЯ 1 ФУНКЦИЯ 2 ФУНКЦИЯ 3 ФУНКЦИЯ 4 ФУНКЦИЯ 5 370.0 ...
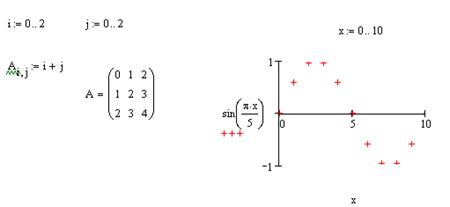
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...
... методы (метод Гаусса). Однако, при решении на ЭВМ систем высокого порядка (более 200 уравнений в системе), предпочтительными являются итерационные методы. Реализация решения задачи анализа линейного стационарного объекта может быть осуществлена с помощью средств матричной алгебры пакета MathCAD. 1.2. Последовательность выполнения работы 1. Согласно номеру варианта (две последние цифры ...
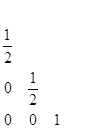
0 комментариев