Способы заполнения магических квадратов

2.                Способы заполнения магических квадратов

 

Магические квадраты нечетного порядка

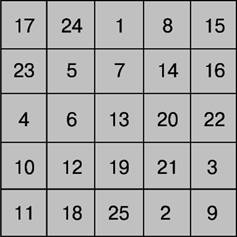
Магические квадраты нечетного порядка можно построить с помощью метода французского геометра 17 в. А.де ла Лубера (сиамский метод). Рассмотрим этот метод на примере квадрата 5-го порядка (рис. 4). Число 1 помещается в центральную клетку верхней строки. Все натуральные числа располагаются в естественном порядке циклически снизу вверх в клетках диагоналей справа налево. Дойдя до верхнего края квадрата, продолжаем заполнять диагональ, начинающуюся от нижней клетки следующего столбца (по ломаной диагонали). Дойдя до правого края квадрата, продолжаем заполнять диагональ, идущую от левой клетки строкой выше. Дойдя до заполненной клетки или угла, траектория спускается на одну клетку вниз, после чего процесс заполнения продолжается.

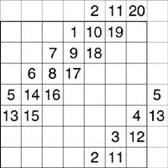
 рис.4

Для облегчения заполнения квадрата данным методом, а именно определения места заполнения следующей клетки, после края квадрата можно воспользоваться следующей схемой

Поставим 1 в среднюю клетку верхнего ряда и продолжим последовательность по диагонали вправо-вверх. Если очередное число на диагонали выходит за границы квадрата, мы его переставляем в соответствующее поле в квадрат (см. рис.5).

Изучая различные источники, мы обратили внимание на то, что можно заполнять квадраты и в другом направлении и не обязательно 1 стоит в данной позиции.

Метод Ф.де ла Ира (1640–1718) основан на двух первоначальных квадратах. На рис. 5 показано, как с помощью этого метода строится квадрат 5-го порядка. В клетку первого квадрата вписываются числа от 1 до 5 так, что число 3 повторяется в клетках главной диагонали, идущей вправо вверх, и ни одно число не встречается дважды в одной строке или в одном столбце. То же самое мы проделываем с числами 0, 5, 10, 15, 20 с той лишь разницей, что число 10 теперь повторяется в клетках главной диагонали, идущей сверху вниз (рис. 5,б). Поклеточная сумма этих двух квадратов (рис. 5,в) образует магический квадрат. Этот метод используется и при построении квадратов четного порядка.

 

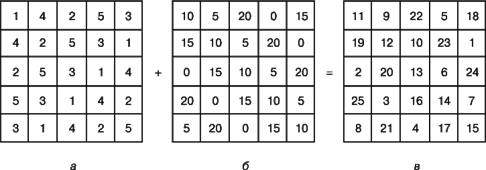
Проанализировав данную схему заполнения по рисунку, мы пришли к следующему алгоритму.

1.                В первом квадрате размещаем числа от 1 до n (порядок квадрата), так, чтобы на побочной диагонали стоял средний элемент этой последовательности.

2.                Все остальные элементы располагаем параллельно этой диагонали по ломаным диагоналям. Элементы на ломаной диагонали равны. Числа в сроке и столбце не должны повторяться.

3.                Во втором квадрате размещаем последовательные числа, кратные порядку квадрата, начиная с 0, (количество элементов равно порядку квадрата) так, чтобы на главной диагонали стоял средний элемент этой последовательности.

4.                Все остальные элементы располагаем параллельно этой диагонали по ломаным диагоналям. Элементы на ломаной диагонали равны.

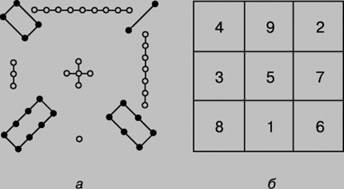
Достраивание до симметричной ступенчатой ромбовидной фигуры

Сначала исходный пустой квадрат достраивается до симметричной ступенчатой ромбовидной фигуры как показано на следующем рисунке.

 

				25
			24		20
		23	6	19	2	15
	22	10	18	1	14	22	10
21		17	5	13	21	9		5
	16	4	12	25	8	16	4
		11	24	7	20	3
			6		2
				1

Полученная на шаге 1 фигура заполняется по косым рядам снизу-вверх-направо целыми числами от 1 до n² последовательно. Результат заполнения показан на следующем рисунке:

				25
			24		20
		23		19		15
	22		18		14		10
21		17		13		9		5
	16		12		8		4
		11		7		3
			6		2
				1

Каждое число, расположенное в фигуре вне исходного квадрата, переносится по вертикали или горизонтали внутрь исходного квадрата в самую удаленную клетку (на n клеток).

Способы заполнения магических квадратов порядка, кратного четырем

Универсальные методы составления магических квадратов произвольного четного порядка пока неизвестны. Однако, разработаны индивидуальные подходы для различных частных случаев. Ниже рассмотрен метод составления магических квадратов, порядок кратен 4. Этот метод удобно рассмотреть на примере магического квадрата 8-го порядка из натуральных чисел от 1 до 64. Метод включает следующую последовательность шагов.

1.                Исходный квадрат делится на соответствующее число квадратов порядка 4. В данном случае таких квадратов будет 4. В каждом подквадрате закрашиваются диагональные элементы (главная и побочная).

2.                Остальные элементы построчно заполняются порядковыми целыми числами в направлении слева -направо и сверху -вниз по закрашенным клеткам и справа -налево и снизу-вверх по не закрашенным клеткам.

3.                Переход между цветами при заполнении происходит, если следующая для заполнения клетка меняет цвет

3.                Реализация способов заполнения магических квадратов

с помощью программы Microsoft Excel.

Так как для составления магических квадратов необходимо всегда проверять контрольные суммы по строкам, столбцам и диагоналям, мы пришли к выводу, что этот процесс лучше автоматизировать. Для автоматизации мы выбрали программу Excel.

Используя функцию автосуммирования, мы подготовили шаблоны для вычисления контрольных сумм магических квадратов 3, 5 и 7 порядка по каждому из методов. А для метода Ф.де ла Ира еще и вычисление элементов третьего квадрата, как сумм соответствующих элементов первых двух квадратов.

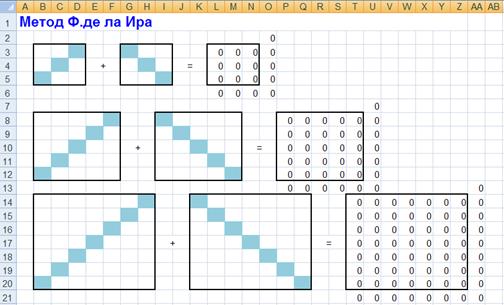
В ходе экспериментальной части по методу Ф.де ла Ира , мы заметили, что в первых двух квадратах, элементы на ломаных диагоналях равны, и пришли в выводу, что процесс заполнения этих квадратов можно также автоматизировать. Достаточно указать только по одному элементу на каждой из ломаной диагонали.

Также для квадрата заданного порядка однозначны элементы на выделенных главных диагоналях, согласно алгоритму заполнения, поэтому их также можно занести в шаблон заполнения.

Внеся эти дополнения в шаблон, мы получили следующую заготовку для магических квадратов:

Теперь достаточно в первом квадрате на главной диагонали (в розовых клетках) разместить элементы с 1 до n. А во втором квадрате в первом столбце (так же в розовых клетках) элементы, кратные порядку квадрата.

В ходе экспериментальной части по способу достраивания до симметричной ступенчатой ромбовидной фигуры, мы заметили, процесс переноса чисел, вышедших за поле квадрата, также можно автоматизировать.

Элементы по диагонали каждый раз увеличиваются на единицу от предыдущего элемента, стоящего в этой диагонали. С учетом этого, достаточно вручную ввести только первые их элементы, а все остальные рассчитать по формулам.

 Внеся эти дополнения в шаблон, мы получили следующую заготовку для магических квадратов данным способом:

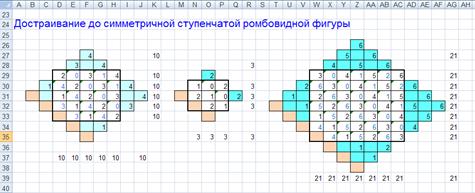
Для построения магического квадрата, в клетки розового цвета внесем первых n чисел, которые при делении на порядок квадрата дают в остатке 1.

Для сиамского метода также можно автоматизировать заполнение и перенос чисел, вышедших за пределы квадрата.

4.                Исследование количества решений магических квадратов.

Изучая литературу по теме, мы установили факт, что с увеличением размеров квадрата быстро растет количество возможных магических квадратов. Так, например, для 3 порядка – единственный, для 4 - 880, для 5 – приближается к четверти миллиона.

Изучив алгоритмы заполнения магических квадратов, нам захотелось экспериментировать: что произойдет, если мы поменяем местами элементы? Получится ли магическая сумма? Получим мы такой же квадрат или другой?

Вот некоторые магические квадраты, полученные методом Ф.де ла Ира.

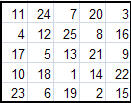
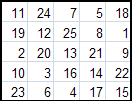
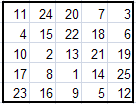
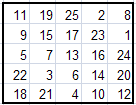
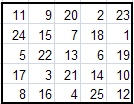
Можно заметить, что все эти квадраты различны. Это только малая доля из всех возможных квадратов. С помощью программы Excel и подготовленных нами шаблонов, на их построение у нас уходит несколько секунд.

Выводы

 

1.                Магический квадрат – древнекитайского происхождения.

2.                Универсального способа заполнения магических квадратов нет.

3.                Способ заполнения магического квадрата, зависит от его порядка.

4.                Для квадратов нечетного порядка существует 3 способа: метод Ф.де ла Ира (на двух квадратах), метод А.де ла Лубера (сиамский метод) и достраивание до симметричной ступенчатой ромбовидной фигуры.

5.                Для квадратов, порядок которых кратен 4 существует способ разбиения на подквадраты порядка 4.

6.                Известные методы для заполнения нечетных квадратов можно автоматизировать. Для этого идеально подходит программа Excel.

7.                Эффективные шаблоны получаются для двух методов: Ф.де ла Ира и достраивания до симметричной ступенчатой ромбовидной фигуры.

8.                С помощью подготовленных нами шаблонов можно создавать различные магические квадраты для одного и того же порядка.

Перспектива

В литературе есть ссылка, что метод, основанный на двух первоначальных квадратах, можно применить и для заполнения квадратов четного порядка. Экспериментируя, мы не пришли к нужному результату и оставляем это для дальнейшего исследования.

Использованные Интернет-ресурсы и литература:

 

1.  http://cad.narod.ru/methods/cadsystems/software/kvadrat.html

2.  http://www.krugosvet.ru/articles/15/1001543/1001543a1.htm

3.  http://ru.wikipedia.org/wiki

4.  И. Я. Депман, Н.Я. Виленкин. За страницами учебника математики. Москва. Просвещение. 1989г.