Навигация
В списке s(G) вершины могут повторяться
1 В списке s(G) вершины могут повторяться.
2 . При восстановлении дерева последнее ребро соединяет вершину yp-2 и оставшуюся в списке 1, 2, …, p вершину не равную yp-2.
Итак, существует взаимно однозначное соответствие между множеством помеченных деревьев с p вершинами и множеством последовательностей вершин s(G). Число таких последовательностей равно, очевидно, pp-2, что и требовалось доказать.
Отметим, что среди pp-2 помеченных деревьев с p вершинами могут быть и изоморфные.
Определение 3. Подграф G1(X1, E1) неориентированного графа G(X, E) называется каркасом, или остовным деревом графа G, если G1 – дерево и X = X1.
Теорема 4. Граф G(X, E) тогда и только тогда обладает каркасом, когда он связен.
Доказательство. Необходимость этого очевидна. Докажем достаточность. Пусть G(X, E) – связный граф. Выясним, есть ли в графе G такое ребро, удаление которого не нарушает связности графа G. Если таких ребер нет, то граф есть дерево в соответствии с теоремой 1. Если же такое ребро, например e, существует, то выбросим его и придем к графу G1(X, E\{e}). Затем указанную процедуру проделываем с графом G1 и т.д. Через конечное число шагов будет построен, очевидно, каркас графа G. Теорема доказана.
Доказательство теоремы дает алгоритм построения некоторого каркаса в связном графе. Однако связный граф может иметь несколько каркасов, поэтому естественно поставить задачу выбора каркаса, удовлетворяющего дополнительным условиям.
Определение 4. Графом с нагруженными ребрами (нагруженным графом) называется неориентированный граф G(X, E), каждому ребру eÎE которого поставлено в соответствие число m(e) ³ 0, называемое весом или длиной ребра e.
Аналогично можно определить нагруженный орграф.
Поставим задачу нахождения такого каркаса G1(X, E1) в нагруженном графе G(X, E), для которого сумма
![]()
минимальна. Каркас с таким свойством называется минимальным каркасом. В соответствии с теоремой 4 каждый нагруженный связный граф обладает минимальным каркасом. Эта задача возникает при проектировании линий связи и электропередач, дорог, трубопроводов и т.п., когда требуется соединить системой каналов связи заданные узлы так, чтобы любые два узла были связаны (возможно, через другие узлы), а общая длина каналов связи была минимальной; при этом узлы можно считать вершинами нагруженного графа, весам ребер которого соответствует длина возможного канала связи между соответствующими узлами. Тогда искомая сеть каналов будет минимальным каркасом этого графа.
Алгоритм построения минимального каркасаПусть G(X, E) - связный нагруженный граф с p вершинами.
Шаг 1 . В качестве первого ребра искомого минимального каркаса выбираем ребро e1 с наименьшим весом m(e1). Если таких ребер несколько, то берем любое из них.
Шаг 2 . В качестве второго ребра берем ребро e2 из множества E\{e1}, имеющее наименьший вес m(e2), и такое, что множество {e1, e2} не содержит простых циклов. Если таких ребер несколько, то берем любое из них.
Шаг 3 . В качестве третьего ребра выбираем такое ребро e3 из множества E\{e1, e2}, которое имеет наименьший вес m(e2) и для которого множество {e1, e2, e3} не содержит простых циклов. Если таких ребер несколько, берем любое из них.
Указанный процесс повторяется и через некоторое число k шагов дает множество E = {e1, e2, …, ek}, к которому нельзя добавить ребро без появления цикла. Подграф G1(X, E1) и является минимальным каркасом графа G(X, E).
Обоснование алгоритмаВ силу свойства 6 из теоремы 1 построенный подграф G1(X, E1) является деревом, поэтому k = p –1. Доказательство минимальности каркаса G1(X, E1) разобьем на два этапа. Пусть сначала G(X, E) – полный граф, у которого веса всех ребер различны, и пусть G2(X, E2) – минимальный каркас графа G. Если E2 ¹ E1, то рассмотрим el – первое из ребер множества E1, не принадлежащее E2. В графе ![]() в силу свойства 6 теоремы 1 существует единственный простой цикл m. Цикл m содержит ребро e0ÏE1. Граф G3(X, E3), где
в силу свойства 6 теоремы 1 существует единственный простой цикл m. Цикл m содержит ребро e0ÏE1. Граф G3(X, E3), где ![]() , не содержит циклов и имеет n – 1 ребро, поэтому он является деревом. Множество {e1, e2, …, el-1, e0} содержится в E2 и поэтому не содержит циклов. Тогда в силу рассмотренного выше алгоритма m(e0) > m(el). Отсюда следует, что суммарный вес дерева G3(X, E3) меньше веса дерева G2(X, E2). Это противоречит минимальности каркаса G2, поэтому E2 = E1 и G1(X, E1) – единственный минимальный каркас графа G.
, не содержит циклов и имеет n – 1 ребро, поэтому он является деревом. Множество {e1, e2, …, el-1, e0} содержится в E2 и поэтому не содержит циклов. Тогда в силу рассмотренного выше алгоритма m(e0) > m(el). Отсюда следует, что суммарный вес дерева G3(X, E3) меньше веса дерева G2(X, E2). Это противоречит минимальности каркаса G2, поэтому E2 = E1 и G1(X, E1) – единственный минимальный каркас графа G.
Пусть теперь G(X, E) – произвольный нагруженный связный граф. Если m(e1) = m(e2), то сделаем замену
m(e1) ® m'(e1) = m(e1) + e,
m(e2) ® m'(e2) = m(e2) + 2e,
взяв такое e, чтобы сохранились соотношения весов m(e1) и m(e2) с другими весами. Сделаем граф G полным, добавив такие ребра di, что ![]() . В полученном графе единственным минимальным каркасом будет каркас, полученный с помощью рассмотренного алгоритма. Легко видеть, что этот каркас будет минимальным и в исходном графе G(X, E).
. В полученном графе единственным минимальным каркасом будет каркас, полученный с помощью рассмотренного алгоритма. Легко видеть, что этот каркас будет минимальным и в исходном графе G(X, E).
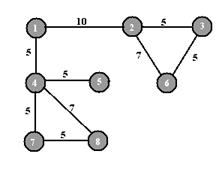
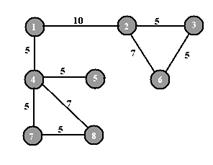
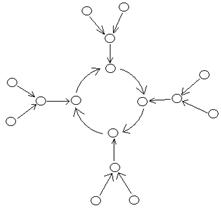
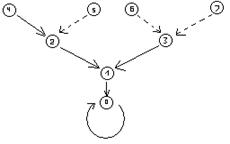
На рис.4 изображены нагруженный граф G и его минимальный каркас G1.

Рис. 4
ЛИТЕРАТУРА
1. Белоусов А.И., Ткачев С.Б. Дискретная математика: Учебник для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко.– М.: изд-во МГТУ им. Н.Э. Баумана, 2001.– 744 с. (Сер. Математика в техническом университете; Вып XIX).
2. Горбатов В.А. Фундаментальные основы дискретной математики. Информационная математика.– М.: Наука, Физматлит, 2000.– 544 с.– ISBN 5-02-015238-2.
Похожие работы
... Если граф G несвязный, он не может иметь остовного дерева, но у него есть остовный лес. Также можно изменить алгоритм нахождения остовного дерева максимального веса, чтобы на выходе получать минимальный остовный лес. остовное дерево алгоритм краскал В алгоритме Краскала используется жадный подход к решению задачи, т.е. в любой момент выполнения данных алгоритмов существует множество ребер E’, ...
... i и j. Для неориентированного графа, матрица смежности имеет размерность (7 х 7) и записывается в виде 1 2 3 4 5 6 7 А= Слева и сверху проставлены номера вершин. Для ориентированного графа, матрица смежности имеет размерность (4 х 4) и записывается в виде 1 2 3 4 А= Матрицу смежности чаще применяют для задания неориентированного графа. Для задания ориентированного ...
... , "базовые" алгоритмы: поиск путей, определение компонент связности графа и т.д. 8. Ввод/вывод графов Одной из проблем при создании средств работы с помеченными графами является выбор внешнего файлового формата для хранения графов. До недавнего времени каждая программная система использовала свой собственный, уникальный формат, что приводило к сложностям при организации обмена данными. ...
... Определить количество циклов и их длину; · Описать множество корней деревьев и т.д. 2. Рассмотреть двумерный вариант клеточного автомата (на клеточном прямоугольнике ) с теми же вопросами, т.е. описать структуру графа состояний. 3. Более подробно рассмотреть матричную интерпретацию. 4. В связи с использованием одномерных клеточных ...


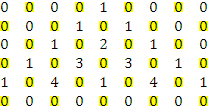
0 комментариев