Навигация
Знайти всі значення параметра а, при яких система рівнянь має розв’язки
7. Знайти всі значення параметра а, при яких система рівнянь має розв’язки

Розв’язання. З першого рівняння системи знайдемо ![]() при
при ![]() . Це рівняння задає сім’ю "півпарабол" (параболи
. Це рівняння задає сім’ю "півпарабол" (параболи ![]() "сковзають" вершинами по вісі абсцис, причому ми розглядаємо лише праву вітку).
"сковзають" вершинами по вісі абсцис, причому ми розглядаємо лише праву вітку).
Ліву частину другого рівняння системи розкладемо на множники. Маємо
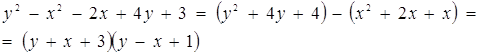
Тільки графіком другого рівняння є об’єднання двох прямих ![]() и
и ![]() .
.
З’ясуємо, при яких значеннях параметра а сім’я "півпарабол" має хоча б одну спільну точку з однією зі знайдених прямих.

Рис.1.1.17
Скористаємося рис.1.1.17. Якщо вершини "півпарабол" знаходяться праворуч від точки А, але ліворуч від точки В (точка В відповідає положенню вершини в момент дотику "півпараболи" з прямою ![]() ), то очевидно графіки спільних точок не мають.
), то очевидно графіки спільних точок не мають.
Якщо вершина розташована в точці А, то очевидно а = −3. Випадок дотику знайдемо, вимагаючи від системи
![]()
мати один Розв’язання, тобто рівняння ![]() повинно мати один корінь. Звідси знаходимо а =
повинно мати один корінь. Звідси знаходимо а = ![]() .
.
Таким чином, початкова система не має розв’язків, якщо ![]() и відповідно має розв’язки, якщо
и відповідно має розв’язки, якщо ![]() та
та ![]() . Відповідь.
. Відповідь. ![]() або
або ![]() .
.
8. Знайти найменше с, при якому система має єдиний розв’язок
![]()
Розв’язання. Перше рівняння системи зручно представити у вигляді ![]() . Це рівняння задає сім’ю кіл постійного радіуса, рівного 1, причому центри кіл лежать на прямій
. Це рівняння задає сім’ю кіл постійного радіуса, рівного 1, причому центри кіл лежать на прямій ![]() . Побудуємо графік функції
. Побудуємо графік функції ![]() (рис.1.1.18). На цьому ж рисунку показано чотири положення кола, при яких початкова система має єдиний Розв’язання.
(рис.1.1.18). На цьому ж рисунку показано чотири положення кола, при яких початкова система має єдиний Розв’язання.
Кожному з відмічених кіл відповідає деяке значення параметра с. Оскільки умова задачі вимагає, щоб с було найменшим, то з чотирьох кіл треба вибрати те, абсциса центра якого приймає найменше значення. Очевидно це буде коло з центром в точці О![]() .
.

Рис.1.1.18
Маємо  . З
. З ![]()
![]() . Звідси
. Звідси ![]() . Тоді з
. Тоді з ![]()
![]() . Таким чином,
. Таким чином,  . Оскільки положенню центра О
. Оскільки положенню центра О![]() відповідає
відповідає ![]() , то знаходимо
, то знаходимо ![]()
Відповідь: ![]()
9. При яких а множиною розв’язків нерівності ![]() є відрізок довжиною
є відрізок довжиною ![]() ?
?
Розв’язання. Графіком функції ![]() є півколо з радіусом, рівним 1, яке "пливе" своїм центром по вісі абсцис. Дана нерівність буде мати Розв’язання тоді, коли точки півкола будуть вище відповідних точок прямої
є півколо з радіусом, рівним 1, яке "пливе" своїм центром по вісі абсцис. Дана нерівність буде мати Розв’язання тоді, коли точки півкола будуть вище відповідних точок прямої ![]() . На рис.1.1.19 показано одно з можливих положень півкола.
. На рис.1.1.19 показано одно з можливих положень півкола.
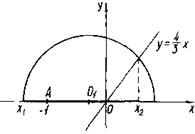
Рис.1.1.19
Для цього випадку розв’язком початкової нерівності буде відрізок ![]() . Умова вимагає, щоб
. Умова вимагає, щоб ![]() .
.
Якщо центр О1 співпадає з точкою A (-1; 0) або розташований ліворуч, то розв’язком нерівності буде відрізок довжиною 2. Разом з тим, якщо О![]() співпадає з точкою O (0; 0) або знаходиться праворуч, то розв’язком нерівності буде відрізок довжиною менше, ніж
співпадає з точкою O (0; 0) або знаходиться праворуч, то розв’язком нерівності буде відрізок довжиною менше, ніж ![]() , або взагалі розв’язків не буде. Дійсно, якщо О1 співпадає з О, то
, або взагалі розв’язків не буде. Дійсно, якщо О1 співпадає з О, то ![]() , a x
, a x![]() - корінь рівняння
- корінь рівняння  Звідси
Звідси ![]() та
та ![]() . Таким чином, потрібне положення центра О
. Таким чином, потрібне положення центра О![]() визначається умовою
визначається умовою ![]() , тобто
, тобто ![]() .
.
Знайдемо значення x![]() та x
та x![]() . Очевидно x
. Очевидно x![]() - найменший корінь рівняння
- найменший корінь рівняння
![]() . Звідси
. Звідси ![]() . В той же час х
. В той же час х![]() - корінь рівняння
- корінь рівняння ![]() Це рівняння рівносильне системі
Це рівняння рівносильне системі

Знайдене рівняння при ![]() має тільки один невід’ємний корінь, тобто.
має тільки один невід’ємний корінь, тобто. 
За умовою 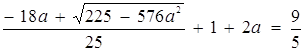 . Розв’язав це рівняння, знаходимо
. Розв’язав це рівняння, знаходимо ![]() ,
, ![]() . Оскільки
. Оскільки ![]() , то
, то ![]() .
.
Відповідь: ![]() .
.
10. Знайти всі значення параметра а, при яких рівняння ![]() має єдиний розв’язок.
має єдиний розв’язок.
Розв’язання. Представимо рівняння у вигляді ![]() . Права частина цього рівняння задає нерухомий "кут", ліва - "кут", вершина якого рухається по вісі абсцис (рис.1.1.20).
. Права частина цього рівняння задає нерухомий "кут", ліва - "кут", вершина якого рухається по вісі абсцис (рис.1.1.20).

Рис.1.1.20
Рівняння буде мати єдиний розв’язок, якщо вершина рухомого "кута"
потрапить або в точку А або в точку В.
Маємо А (-4; 0), В (-2; 0), і координати цих точок задовольняють рівнянню ![]() . Тоді
. Тоді ![]() або
або ![]() . Звідси
. Звідси ![]() або
або ![]() .
.
Відповідь: ![]() або
або ![]() .
.
11. Знайти всі значення параметра а, для яких найменше значення функції ![]() більше 2.
більше 2.
Розв’язання. Дана функція не задає сім’ю "кутів". За умовою задачі необхідно шукати значення параметра, при яких нерівність ![]() виконується при будь-яких х. Це і є формулювання, рівносильна даній.
виконується при будь-яких х. Це і є формулювання, рівносильна даній.
Одержану нерівність слід переписати так: ![]() .
.
"Кут" ![]() повинен бути розташований так, щоб на параболі
повинен бути розташований так, щоб на параболі ![]() не знайшлося ні однієї точки, яка б лежала вище відповідних точок "кута" або на самому "куті". Для цього вершина "кута" не повинна належати відрізку
не знайшлося ні однієї точки, яка б лежала вище відповідних точок "кута" або на самому "куті". Для цього вершина "кута" не повинна належати відрізку ![]() (рис.1.1.21).
(рис.1.1.21).

Рис.1.1.21
Абсциси а1 и а2 відповідають моменту дотику. Таким чином, шукані значення параметра визначаються сукупністю нерівностей ![]() або
або ![]() . Залишилось знайти
. Залишилось знайти ![]() та
та ![]() . Значення
. Значення ![]() та
та ![]() знайдемо, вимагаючи відповідно від рівнянь
знайдемо, вимагаючи відповідно від рівнянь ![]()
![]() мати
мати
єдиний корінь. Звідси ![]()
![]() .
.
Відповідь: ![]() або
або ![]() .
.
12. При яких а множиною розв’язків нерівності ![]() є відрізок числової прямої?
є відрізок числової прямої?
Розв’язання. Маємо ![]() . Права частина цієї нерівності задає сім’ю "кутів", вершини яких лежать на прямій у = 3 (рис.1.1.22).
. Права частина цієї нерівності задає сім’ю "кутів", вершини яких лежать на прямій у = 3 (рис.1.1.22).

Рис.1.1.22
Якщо вершина "кута" знаходиться між точками А та В, то обов’язково знайдуться проміжки області визначення, на яких графік лівої частини нерівності не вище графіка правої частини. На рис.1.1.22 показано одно з проміжних положень "кута" з вершиною С. В цьому випадку розв’язком початкової нерівності будуть всі точки відрізку MN.
При ![]() вершина "кута" знаходиться між точками А та В, і виникає бажання вважати проміжок (-8;
вершина "кута" знаходиться між точками А та В, і виникає бажання вважати проміжок (-8;
4) шуканою відповіддю. Але умова задачі вимагає, щоб розв’язком нерівності був відрізок числової прямої. А якщо вершина "кута" співпадає з будь-якою з точок відрізка EF, включаючи Е і не включаючи F (рис.1.1.23, точка F відповідає моменту дотику), то розв’язком нерівності буде або відрізок і точка, або два відрізки. Визначив координати точок Е та F, знаходимо  .
.

Рис.1.1.23
Відповідь:  .
.
1.2 Поворот
В цьому параграфі вибір сім’ї кривих не є різноманітним, а точніше він одноваріантний: члени сім’ї кривих ![]() - прямі. Більш того, центр повороту належить прямій. Іншими словами, ми обмежимося сім’єю виду
- прямі. Більш того, центр повороту належить прямій. Іншими словами, ми обмежимося сім’єю виду ![]() , де
, де ![]() - центр повороту.
- центр повороту.
Такий вибір обумовлено тим, що в рівності ![]() складно побачити аналітичне задання повороту кривих, які відрізняються від прямих. Тому про поворот, як про метод, доцільно говорити лише для прямих вказаного типа.
складно побачити аналітичне задання повороту кривих, які відрізняються від прямих. Тому про поворот, як про метод, доцільно говорити лише для прямих вказаного типа.
1. При яких ![]() рівняння
рівняння ![]() має три розв’язки?
має три розв’язки?
Розв’язання. Побудуємо графіки функцій ![]() та
та ![]() . Прямі
. Прямі ![]() переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).
переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).
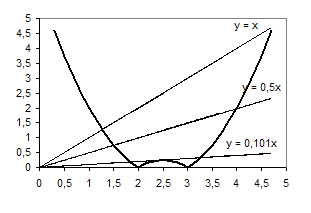
Рис.1.2.1
Рівняння буде мати три розв’язки, коли пряма ![]() перетинає параболу в двох точках і дотикається до вершини, тобто коли
перетинає параболу в двох точках і дотикається до вершини, тобто коли ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Обираємо ![]() , так як при
, так як при ![]() пряма дотикається вітки гіперболи нижче вісі абсцис.
пряма дотикається вітки гіперболи нижче вісі абсцис.
Відповідь: ![]()
2. Розв’язати рівняння ![]() і визначити значення
і визначити значення ![]() , при яких воно має єдиний розв’язок.
, при яких воно має єдиний розв’язок.
Розв’язання. Побудуємо графіки функцій ![]() та
та ![]() . Прямі
. Прямі ![]() переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).
переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).

Рис.1.2.2
Якщо ![]() , то
, то ![]() , звідки
, звідки ![]()
Якщо ![]() , то
, то ![]() , звідки
, звідки ![]()
Знайдемо параметр ![]() :
: ![]() , звідки
, звідки ![]() , тобто
, тобто ![]() .
.
![]() , звідки
, звідки ![]() , тобто
, тобто ![]() та
та ![]() .
.
Відповідь: при ![]()
![]() ; при
; при ![]()
![]() або
або ![]() ; при
; при ![]() або
або ![]()
![]() .
.
3. При яких значеннях ![]() рівняння
рівняння ![]() має одно, два, три чотири розв’язки?
має одно, два, три чотири розв’язки?
Розв’язання. Побудуємо графіки функцій ![]() та
та ![]() . Прямі
. Прямі ![]() переходять друг в друга шляхом перетворення повороту з центром в точці О (9; 0).
переходять друг в друга шляхом перетворення повороту з центром в точці О (9; 0).
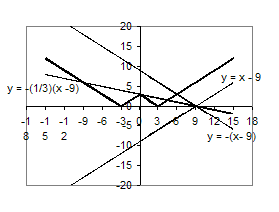
Рис.1.2.3
З рисунка видно, що при ![]() рівняння має 1 розв’язок, при
рівняння має 1 розв’язок, при ![]() - 2 розв’язки, при
- 2 розв’язки, при ![]() - 3 розв’язки, при
- 3 розв’язки, при ![]() - 4 розв’язки, при
- 4 розв’язки, при ![]() - 2 розв’язки, при
- 2 розв’язки, при ![]() - 1 розв’язок.
- 1 розв’язок.
Відповідь: при ![]() - 1 розв’язок, при
- 1 розв’язок, при ![]() - 2 розв’язки, при
- 2 розв’язки, при ![]() - 3 розв’язки, при
- 3 розв’язки, при ![]() - 4 розв’язки, при
- 4 розв’язки, при ![]() - 2 розв’язки, при
- 2 розв’язки, при ![]() - 1 розв’язок.
- 1 розв’язок.
4. При яких значеннях ![]() рівняння
рівняння ![]() має рівно 1 розв’язок? Знайти його.
має рівно 1 розв’язок? Знайти його.
Розв’язання. Запишемо ОДЗ рівняння: 
Побудуємо графіки функцій ![]() та
та ![]() враховуючи ОДЗ.
враховуючи ОДЗ.
Прямі ![]() переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).
переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).

Рис.1.2.4
Рівняння можна переписати у вигляді: ![]() ,
, ![]() . Знайдемо
. Знайдемо ![]() .
.
Якщо ![]() , то маємо 1 розв’язок:
, то маємо 1 розв’язок: ![]() ,
, ![]() . Значення
. Значення ![]() відкидаємо згідно з ОДЗ. Для
відкидаємо згідно з ОДЗ. Для ![]() розв’язок
розв’язок ![]() .
.
Якщо ![]() , то маємо 2 розв’язки:
, то маємо 2 розв’язки: 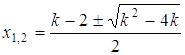 . Згідно з ОДЗ
. Згідно з ОДЗ ![]() , тобто
, тобто  , звідки
, звідки ![]() .
.
Відповідь: при ![]()
![]() , при
, при ![]()
 .
.
5. При яких ![]() рівняння
рівняння ![]() має розв’язки?
має розв’язки?
Розв’язання. Запишемо ОДЗ рівняння: 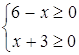 , звідки
, звідки ![]() . Побудуємо графіки функцій
. Побудуємо графіки функцій ![]() та
та ![]() .
.
Прямі ![]() переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).
переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).

Рис.1.2.5
З рисунка видно, що при ![]() та
та ![]() рівняння має розв’язки.
рівняння має розв’язки.
Відповідь: ![]() та
та ![]() .
.
6. Знайти значення ![]() , при яких рівняння
, при яких рівняння ![]() має тільки один розв’язок.
має тільки один розв’язок.
Розв’язання. Запишемо ОДЗ рівняння:
 ,
,  .
.
Перепишемо рівняння у вигляді: ![]() . Побудуємо графіки функцій
. Побудуємо графіки функцій ![]() та
та ![]() . Прямі
. Прямі ![]() переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0). Розв’язуємо рівняння:
переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0). Розв’язуємо рівняння: ![]() ,
, ![]()
Точку дотику двох функцій знайдемо з умови: ![]() , тоді
, тоді ![]() ,
, ![]() .
.
Інші значення параметра ![]() знайдемо з ОДЗ:
знайдемо з ОДЗ: ![]() , звідки
, звідки ![]() .
.

Рис.1.2.6
Відповідь: ![]() ,
, ![]() .
.
7. При яких значеннях ![]() рівняння
рівняння ![]() має єдиний розв’язок?
має єдиний розв’язок?
Розв’язання. Знайдемо ОДЗ рівняння:
 ,
,  .
.
Перепишемо рівняння у вигляді ![]() ,
, ![]() . Побудуємо графіки функцій
. Побудуємо графіки функцій ![]() та
та ![]() , враховуючи ОДЗ.
, враховуючи ОДЗ.

Рис.1.2.7
Знайдемо точку дотику двох графіків функцій: ![]() ;
; ![]() ;
; ![]() ,
, ![]() ,
, ![]() .
.
Також з рисунка видно, що рівняння буде мати єдиний розв’язок при ![]() .
.
Відповідь: ![]() або
або ![]() .
.
8. Знайти всі значення параметра ![]() , при яких найменше значення функції
, при яких найменше значення функції ![]() менше 2.
менше 2.
Розв’язання. Переформулюємо задачу: знайти ![]() , при яких нерівність
, при яких нерівність ![]() має хоча б один розв’язок.
має хоча б один розв’язок.
Перепишемо нерівність у вигляді: ![]() . Побудуємо графіки функцій
. Побудуємо графіки функцій ![]() та
та ![]() . На рис.31 наведені графік функції
. На рис.31 наведені графік функції ![]() та дві прямі сім’ї
та дві прямі сім’ї ![]() .
.
Положенню І відповідає ![]() (
(![]() проходе через точку (-4,0)), а положенню ІІ (момент дотику:
проходе через точку (-4,0)), а положенню ІІ (момент дотику: ![]() ,
, ![]() ) відповідає
) відповідає ![]() . Нерівність буде мати розв’язки, якщо прямі І та ІІ “крутити” відповідно за та проти годинникової стрілки до вертикального положення.
. Нерівність буде мати розв’язки, якщо прямі І та ІІ “крутити” відповідно за та проти годинникової стрілки до вертикального положення.

Рис.1.2.8
Відповідь: ![]() або
або ![]() .
.
Задачі для самостійної роботи
Похожие работы
... . Лише за наявності відповідної математичної підготовки слід вимагати від учнів запис та формулювання законв заломлення світла. У новій програмі з фізики для 12 – річної школи багато уваги приділено розв’язуванню фізичних задач. Так, підкреслено , що задачі потрібно ефективно використовувати на всіх етапах засвоєння фізичного знання : для розвитку інтересу, творчіх здібностей і мотивації учнів ...
... іну: , де . Двічі диференціюючи цю функцію і підставляючи вирази для похідних у рівняння (11.59), отримаємо крайову задачу з однорідними граничними умовами: , , . (11.71) Постановка задачі Щоб знайти єдиний розв'язок звичайного диференціального рівняння, необхідно задати деякі допоміжні умови, що використовуються для обчислення інтегрування. Для рі ...
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...
... що знаходяться в стані рівноваги. Для одержання остаточних висновків і підвищення вірогідності застосовуються методи математичного аналізу і математичного моделювання. Розділ ІІ 2.1 Міжпредметні зв’язки при розв’язуванні хімічних задач «Рішення задач – визнаний засіб розвитку мислення, яке легко поєднується з іншими засобами і прийомами навчання» (Цитович І.К.). При вивченні курсу хімії ...



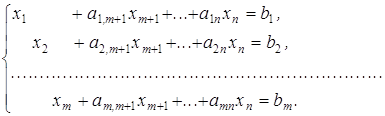
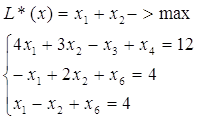

0 комментариев