Навигация
Вариационные задачи с подвижными границами
2. Вариационные задачи с подвижными границами
2.1 Простейшая задача с подвижными границами
В гл. 1 при исследовании функционала
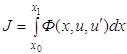
предополагается, что граничные точки ![]() заданы.
заданы.
Предположим теперь, что одна или обе граничные точки могут перемещаться, тогда класс допустимых кривых расширяется. Поэтому, если на какой-нибудь кривой ![]() достигается экстремум в задаче с подвижными граничными точками, то экстремум тем более достигается по отношению к более узкому классу кривых, имеющих общие граничные точки с кривой
достигается экстремум в задаче с подвижными граничными точками, то экстремум тем более достигается по отношению к более узкому классу кривых, имеющих общие граничные точки с кривой ![]() , и, следовательно, должно быть выполнено основное, необходимое для достижения экстремума в задаче с неподвижными границами условие – функция
, и, следовательно, должно быть выполнено основное, необходимое для достижения экстремума в задаче с неподвижными границами условие – функция ![]() должна быть решением уравнения Эйлера:
должна быть решением уравнения Эйлера:
![]() .
.
Итак, кривые ![]() , на которых реализуется экстремум в задаче с подвижными границами, должны быть экстремалями.
, на которых реализуется экстремум в задаче с подвижными границами, должны быть экстремалями.
Общее решение уравнения Эйлера содержит две произвольные постоянные, для определения которых необходимо иметь два условия. В задаче с неподвижными граничными точками такими условиями были
![]() ,
, ![]() .
.
В задаче с подвижными границами одно или оба эти условия отсутствуют и недостающие условия для определения произвольных постоянных общего решения уравнения Эйлера должны быть получены из основного необходимого условия экстремума ![]() , так как в задаче с подвижными границами экстремум достигается лишь на решениях
, так как в задаче с подвижными границами экстремум достигается лишь на решениях ![]() уравнения Эйлера, то в дальнейшем можно рассматривать значение функционала лишь на функциях этого семейства. При этом функционал
уравнения Эйлера, то в дальнейшем можно рассматривать значение функционала лишь на функциях этого семейства. При этом функционал ![]() превращается в функцию параметров
превращается в функцию параметров ![]() и
и ![]() и пределов интегрирования
и пределов интегрирования ![]() ,
, ![]() , а вариация функционала совпадает с дифференциалом этой функции. Для упрощения будем считать, что одна из этих точек, например
, а вариация функционала совпадает с дифференциалом этой функции. Для упрощения будем считать, что одна из этих точек, например ![]() , закреплена, а другая
, закреплена, а другая ![]() может перемещаться и переходить в точку
может перемещаться и переходить в точку ![]() , или, как обычно обозначают в вариационном исчислении,
, или, как обычно обозначают в вариационном исчислении, ![]() .
.
Допустимые кривые ![]() и
и ![]() будем считать близкими, если модули вариаций
будем считать близкими, если модули вариаций ![]() и
и ![]() малы и малы модули приращений
малы и малы модули приращений ![]() и
и ![]() .
.
Экстремали, проходящие через точку ![]() , образуют пучок экстремалей
, образуют пучок экстремалей ![]() . Функционал
. Функционал ![]() на кривых этого пучка превращается в функцию
на кривых этого пучка превращается в функцию ![]() и
и ![]() . Если кривые пучка не пересекаются, то этот функционал можно рассматривать как однозначную функцию
. Если кривые пучка не пересекаются, то этот функционал можно рассматривать как однозначную функцию ![]() и
и ![]() (рис. 3.1).
(рис. 3.1).
2.2 Условие трансверсальности
|
|
Вычислим вариацию функционала ![]() на экстремалях пучка
на экстремалях пучка ![]() при перемещении граничной точки из положения
при перемещении граничной точки из положения ![]() в положение
в положение ![]() . Так как функционал
. Так как функционал ![]() на кривых пучка превратился в функцию
на кривых пучка превратился в функцию ![]() и
и ![]() , то его вариация совпадает с дифференциалом этой функции. Выделим из приращения
, то его вариация совпадает с дифференциалом этой функции. Выделим из приращения ![]() главную линейную по отношению к
главную линейную по отношению к ![]() и
и ![]() часть:
часть:
 (3.1)
(3.1)
Первое слагаемое правой части преобразует с помощью теоремы о среднем значении:
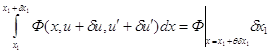 , где
, где ![]() .
.
В силу непрерывности функции ![]() будем иметь:
будем иметь:
![]()
 ,
,
где ![]() при
при ![]() ,
, ![]() .
.
Итак,
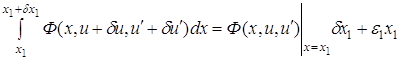 .
.
Второе слагаемое (3.1) преобразуем путем разложения подинтегральной функции по формуле Тейлора

где ![]() является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем ![]() или
или ![]() . В свою очередь линейная часть
. В свою очередь линейная часть

может быть преобразована путем интегрирования по частям второго слагаемого подинтегральной функции к виду
 .
.
Значение функционала берется лишь на экстремалях, следовательно
 . Так как граничная точка
. Так как граничная точка ![]() закреплена, то
закреплена, то 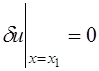 . Следовательно,
. Следовательно,
 .
.
Итак, окончательно имеем:


где приближенные равенства также справедливы с точностью до членов порядка выше первого относительно ![]() и
и ![]() .
.
Таким образом
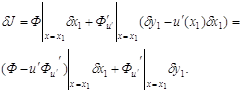
Основное необходимое условие экстремума ![]() приобретает вид
приобретает вид
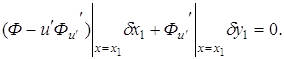 (3.2)
(3.2)
Если вариации ![]() и
и ![]() независимы, то получаем
независимы, то получаем
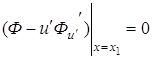 и
и 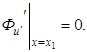
Однако чаще всего вариации ![]() и
и ![]() бывают зависимы. Пусть, например, правая граничная точка
бывают зависимы. Пусть, например, правая граничная точка ![]() может перемещаться по некоторой кривой
может перемещаться по некоторой кривой
![]()
Тогда ![]() и условие (3.2) принимает вид
и условие (3.2) принимает вид

или, так как ![]() изменяется произвольно, то
изменяется произвольно, то
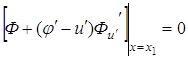 . (3.3)
. (3.3)
Это условие устанавливает зависимость между угловыми коэффициентами ![]() и
и ![]() в граничной точке. Оно называется условием трансверсальности.
в граничной точке. Оно называется условием трансверсальности.
Условие трансверсальности совместно с условием ![]() позволяет определить одну или несколько экстремалей пучка
позволяет определить одну или несколько экстремалей пучка ![]() , на которых может достигаться экстремум.
, на которых может достигаться экстремум.
Пример. Найти условие трансверсальности для функционалов вида
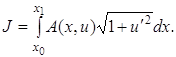
Условие трансверсальности (3.3) имеет в данном случае вид

или
![]()
Полагая, что ![]() в граничной точке, получим
в граничной точке, получим
![]()
или
![]() .
.
Условие трансверсальности в данном случае свелось к условию ортогональности.
2.3 Задача с подвижными границами для функционалов от нескольких функций
Если при исследовании на экстремум функционала
 (3.4)
(3.4)
одна из граничных точек, например ![]() перемещается (
перемещается (![]() ,
, ![]() ), а другая,
), а другая, ![]() , неподвижна, то экстремум может достигаться лишь на интегральных кривых системы уравнений Эйлера
, неподвижна, то экстремум может достигаться лишь на интегральных кривых системы уравнений Эйлера
![]() ,
, ![]()
![]() (3.5)
(3.5)
Общее решение системы уравнений Эйлера содержит четыре произвольные постоянные. Зная координаты граничной точки ![]() , которую считаем неподвижной, можно исключить две произвольные постоянные. Для определения двух других произвольных постоянных необходимо иметь еще два уравнения, которые могут быть получены из условия
, которую считаем неподвижной, можно исключить две произвольные постоянные. Для определения двух других произвольных постоянных необходимо иметь еще два уравнения, которые могут быть получены из условия ![]() , при условии, что функционал задается лишь на решениях системы уравнений Эйлера (3.5). При этом функционал
, при условии, что функционал задается лишь на решениях системы уравнений Эйлера (3.5). При этом функционал ![]() превращается в функцию координат
превращается в функцию координат ![]() точки
точки ![]() и вариация функционала превращается в дифференциал этой функции. Если экстремали пучка с центром в точке
и вариация функционала превращается в дифференциал этой функции. Если экстремали пучка с центром в точке ![]() не пересекаются, то эта функция будет однозначной.
не пересекаются, то эта функция будет однозначной.
Вычисление вариации ![]() проводится аналогично тому, как это делалось в 3.2:
проводится аналогично тому, как это делалось в 3.2:
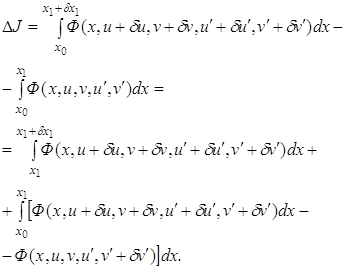
Применяя теорему о среднем значении к первому интегралу и учитывая непрерывность функции ![]() , выделив главную линейную часть с помощью формулы Тейлора во втором интеграле и используя равенства (3.5), получим
, выделив главную линейную часть с помощью формулы Тейлора во втором интеграле и используя равенства (3.5), получим
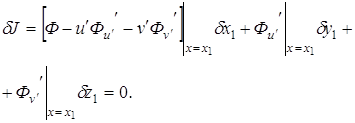 (3.6)
(3.6)
Откуда, учитывая зависимость ![]() ,
, ![]() ,
, ![]() , получим
, получим
 ,
, 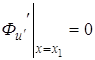 и
и 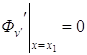 .
.
Если граничная точка ![]() может перемещаться по некоторой кривой
может перемещаться по некоторой кривой ![]() ,
, ![]() , то
, то
![]() ,
, ![]() , и условие
, и условие ![]() (3.6)
(3.6)
переходит в условие (считая ![]() произвольным).
произвольным).
 (3.7)
(3.7)
Это условие носит название условия трансверсальности в задаче об исследовании на экстремум функционала (3.4).
Условие (3.7) совместно с уравнениями ![]() ,
, ![]() дает недостающие уравнения для определения произвольных постоянных в общем решении системы уравнений Эйлера.
дает недостающие уравнения для определения произвольных постоянных в общем решении системы уравнений Эйлера.
Если граничная точка ![]() может перемещаться по некоторой поверхности
может перемещаться по некоторой поверхности ![]() , то
, то ![]() , причем вариации
, причем вариации ![]() и
и ![]() произвольны. Следовательно, условие (3.6) в силу независимости
произвольны. Следовательно, условие (3.6) в силу независимости ![]() и
и ![]() дает
дает
 ,
,
 (3.8)
(3.8)
Если рассматривать функционал
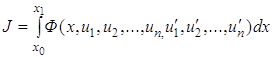 ,
,
то в случае одной подвижной точки ![]() в этой точке
в этой точке

Пример. Найти условие трансверсальности для функционала
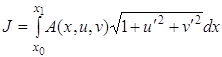 ,
,
если ![]() .
.
Условия трансверсальности (3.8) в данном случае имеют вид
![]() и
и ![]() при
при ![]() или
или ![]() при
при ![]() т.е. являются условиями параллельности вектора касательной
т.е. являются условиями параллельности вектора касательной ![]() к искомой экстремали в точке
к искомой экстремали в точке ![]() и вектора нормали
и вектора нормали ![]() к поверхности
к поверхности ![]() в той же точке. Следовательно, усливие трансверсальности становится в данном случае условием ортоганальности экстремали к поверхности
в той же точке. Следовательно, усливие трансверсальности становится в данном случае условием ортоганальности экстремали к поверхности ![]() .
.
1. Найти экстремаль функционала ![]() при заданных краевых условиях на концах отрезка
при заданных краевых условиях на концах отрезка ![]() . Считается, что
. Считается, что ![]() .
.
Пример 1.
![]() ,
, ![]() ,
, ![]() .
.
Решение:
Вычислим первую вариацию функционала ![]()
![]() .
.
После преобразования этого функционала получим
![]() .
.
Произвольные функции ![]() и удовлетворяют условию
и удовлетворяют условию ![]() .
.
В точке ![]() предполагаемого экстремума функционала
предполагаемого экстремума функционала ![]() должно выполняться необходимое условие
должно выполняться необходимое условие ![]() , поэтому уравнение Эйлера будет иметь вид
, поэтому уравнение Эйлера будет иметь вид
![]()
Это уравнение приводится к виду
![]()
и должно решаться при условии ![]() ,
, ![]() .
.
Имеем
![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
![]()
откуда ![]() ,
, ![]() .
.
Таким образом, получаем решение ![]() .
.
Исследовать функционал ![]() , заданный на отрезке
, заданный на отрезке ![]() , на экстремум. При заданных краевых условиях считается, что
, на экстремум. При заданных краевых условиях считается, что ![]() .
.
Пример 2.
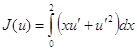 ,
, ![]() ,
, ![]() .
.
Решение. Найдем первую вариацию функционала ![]()
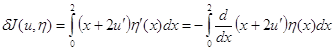
Необходимое условие экстремума функционала в точке ![]() даёт уравнение Эйлера
даёт уравнение Эйлера
![]() .
.
Это уравнение при краевых условиях ![]() ,
, ![]() дает решение
дает решение
![]() .
.
Так как в данном примере
![]() , то
, то
![]() ,
, ![]() ,
, ![]() ,
, ![]()
и усиленное условие Лежандра
![]() выполняется.
выполняется.
Уравнение Эйлера для интеграла (1.39) (см. 1.8.) будет иметь вид (после замены ![]() на
на ![]() )
)
![]()
или
![]()
Откуда
![]() ,
, ![]() .
.
Для нахождения ![]() ,
, ![]() имеем условия
имеем условия ![]() ,
, ![]() .
.
Откуда
![]() ,
, ![]() .
.
Проверим условие Якоби. Решение ![]() на интервале
на интервале ![]() положительно. Следовательно, усиленное условие Якоби выполняется. Отсюда делаем заключение, что экстремаль
положительно. Следовательно, усиленное условие Якоби выполняется. Отсюда делаем заключение, что экстремаль ![]() дает функционалу
дает функционалу
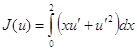
сильный (абсолютный) минимум.
Список используемой литературы
1. Гельфанд И.М., Фомин С.В. Вариационное исчисление. М.: Наука. 1961.
2. Коршунов Ю.М., «Математические основы кибернетики», Москва, 1987 г.;
3. Таха Х., «Введение в исследование операций», Москва, 1985 г.;
4. Д. Сю., А. Мейер, «Современная теория автоматического управления и её применение», Машиностроение, 1972 г.;
Похожие работы
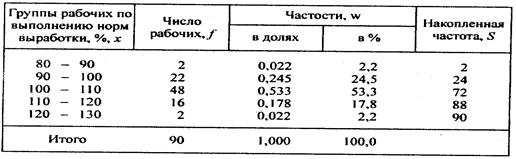
... , а также для сравнения степени вариации одноименных признаков в нескольких совокупностях исчисляется относительный показатель вариации — коэффициент вариации (V), который представляет; собой процентное отношение среднего квадратического отклонения к средней арифметической: По величине коэффициента вариации можно судить о степени вариации признаков, а следовательно, об однородности состава ...
... предложения и представляет равновесную цену в каждый период времени. Предположим также, что все прочие внешние факторы ценообразования, кроме налогов, в рассматриваемый период времени остаются неизменными. Р Q Рис.12. Воздействие изменения налога на кривые спроса ...
... ), интересующей органы внутренних дел, и необходимой им для выполнения возложенных задач. При этом необходимо учесть оперативную специфику работы правоохранительных органов. В современных условиях важное значение для выявления, пресечения и расследования налоговых преступлений приобретают сведения о хозяйственной деятельности налогоплательщика, получившие отражение в бухгалтерской документации ...
... основными производственными фондами (факторный признак - х) по данным задачи 1 вычислите коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение. 5. ПРАКТИКУМ ПО ТЕОРИИ СТАТИСТИКИ 1. ГРУППИРОВКА СТАТИСТИЧЕСКИХ ДАННЫХ И ЕЕ РОЛЬ В АНАЛИЗЕ ИНФОРМАЦИИ Одним из основных наиболее распространенных методов обработки и анализа первичной статистической информации ...
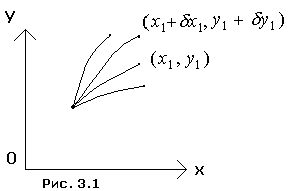







0 комментариев