Кратные множители

5. Кратные множители

Существуют методы, позволяющие узнать, обладает ли данный многочлен кратными множителями, и в случае положительного ответа дающие возможность свести изучение этого многочлена к изучению многочленов, уже не содержащих кратных множителей.

Теорема. Если  является  - кратным неприводимым множителем многочлена , , то он будет - кратным множителем производной этого многочлена. В частности, простой множитель многочлена. Не входит в разложение производной.

В самом деле, пусть

, (5.1)

причем  уже не делится на . Дифференцируя равенство (5.1), получаем:

.

Второе из слагаемых, стоящих в скобках, не делится на . Действительно,  не делится по условию,  имеет меньшую степень, т.е. также не делится на . С другой стороны, первое слагаемое суммы, стоящей в квадратных скобках, делиться на, т.е. множитель , на самом деле входит в  с кратностью .

Из данной теоремы и из указанного выше способа разыскания наибольшего общего делителя двух многочленов следует, что если дано разложение многочлена  на неприводимые множители:

, (5.2)

то наибольший общий делитель многочлена  и его производной обладает следующим разложением на неприводимые множители:

,  (5.3)

где множитель  следует при  заменять единицей. В частности, многочлен  тогда и только тогда не содержит кратных множителей, если он взаимно прост со своей производной.

  5.1. Выделение кратных множителей

Если дан многочлен  с разложением (5.2) и если через  мы обозначим наибольший общий делитель  и его производной  то (5.3) будет разложением для . Деля (5.2) на (5.3), мы получим:

т.е. получим многочлен, не содержащий кратных множителей, причем всякий неприводимый множитель для , имеющего вообще говоря, меньшую степень и, во всяком случае, содержащего лишь простые множители. Если эта задача для  будет решена, то останется определить лишь кратность найденных неприводимых множителей в , что достигается применением алгоритма деления.

Усложняя изложенный сейчас метод, можно сразу перейти к рассмотрению нескольких многочленов без кратных множителей, причем, найдя неприводимые множители этих многочленов, мы не только найдем все неприводимые множители для , но и будем знать их кратность.

Пусть (5.2) будет разложением  на неприводимые множители, причем наивысшая кратность множителей есть , . Обозначим через  произведение всех однократных множителей многочлена , через  - произведение всех двукратных множителей, но взятых лишь по одному разу, и т.д., наконец  - произведение всех -кратных множителей, также взятых лишь по одному разу; если при этом для некоторого  в  отсутствуют -кратные множители, то полагаем . Тогда  будет делиться на - тую степень многочлена  и разложение (5.2) примет вид

 

а разложение (5.3) для  перепишется в виде

обозначая через  наибольший общий делитель многочлена  и его производной и вообще через  наибольший общий делитель многочленов  и , таким путем получим:

……………………………

.

Отсюда

,

……………………………

,

И поэтому, наконец,

, , …,

Таким образом, пользуясь лишь приемами, не требующими знания неприводимых множителей многочлена , а именно взятием производной, алгоритмом Евклида и алгоритмом деления, мы можем найти многочлены  без кратных множителей, причем всякий неприводимый множитель многочлена  , будет -кратным для .

Пример. Разложить многочлен  на кратные множители.

 │

 

│

 

 │

 

  

│

 │

 

 

│ 

 

│

│

│ 

Многочлен  имеет разложение в виде .

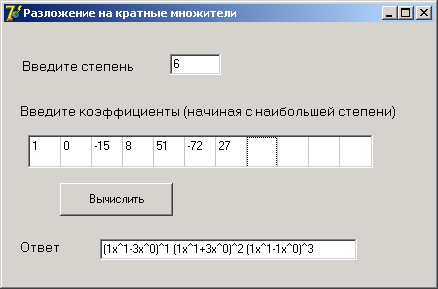
Я составила программу для разложения многочлена на кратные множители.

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, Grids;

type

TForm1 = class(TForm)

Edit1: TEdit;

Label1: TLabel;

SGd1: TStringGrid;

Label2: TLabel;

Button1: TButton;

Label3: TLabel;

SGd2: TStringGrid;

SGd3: TStringGrid;

SGd4: TStringGrid;

Edit6: TEdit;

procedure Button1Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

c,i,st1,st2,stiz,n_iz,n_nod,n,m,d_st,step,f:integer;

k,d,s:string;

kof1,kof2,k1,k2,izubst,a,b,a2,b2,buf,est,fxst:array[0..15] of integer;

izub,e,fx:array[0..50,0..50] of integer;

first:boolean;

implementation

{$R *.dfm}

procedure TForm1.Button1Click(Sender: TObject);

var i,j,k_1,st3,l:integer;

sokr:boolean;

k2_2,k1_1:array[0..10] of integer;

begin

st1:=StrToInt(Edit1.Text);

for i:=0 to st1 do begin

SGd4.Cells[i,0]:=SGd1.Cells[i,0];

end;

repeat

n_iz:=n_iz+1;

st2:=st1-1;

for i:=0 to st1 do begin

if SGd1.Cells[i,0]<>'' then

kof1[st1-i]:=StrToInt(SGd1.Cells[i,0])

else MessageDlg('Внимание! Не введены значения коэффициентов!',mtWarning,[mbOK],0);

end;

s:='f(x)=';

for i:=st1 downto 0 do begin

if kof1[i]<>0 then begin

if(kof1[i-1]<0)or(i=0) then begin

str(kof1[i],d);

str(i,k);

s:=s+d+'x^'+k;

end

else begin

str(kof1[i],d);

str(i,k);

s:=s+d+'x^'+k+'+';

end;

end;

kof2[i-1]:=kof1[i]*i;

end;

//Edit2.Text:=s;

s:='f1(x)=';

for i:=st2 downto 0 do begin

SGd2.Cells[st2-i,0]:=inttostr(kof2[i]);

if kof2[i]<>0 then begin

if(kof2[i-1]<0)or(i=1) then begin

str(kof2[i],d);

str(i-1,k);

s:=s+d+'x^'+k;

end

else begin

str(kof2[i],d);

str(i-1,k);

s:=s+d+'x^'+k+'+';

end;

end;

//Edit3.Text:=s;

end;

for i:=0 to st1 do begin

kof1[i]:=StrToInt(SGd1.Cells[i,0]);

k1[i]:=StrToInt(SGd1.Cells[i,0]);

end;

for i:=0 to st2 do begin

kof2[i]:=StrToInt(SGd2.Cells[i,0]);

k2[i]:=StrToInt(SGd2.Cells[i,0]);

end;

while kof2[0]<>0 do begin

repeat

//Edit4.Text:='';

stiz:=0;

k_1:=k1[0];

if k1[0]<>kof2[0] then begin

if (k1[0] mod kof2[0])=0 then begin

for j:=0 to st2 do

k2[j]:=(k1[0] div kof2[0])*kof2[j];

end

else begin

if k2[0]<>1 then

for j:=0 to st1 do

k1[j]:=kof2[0]*k1[j];

if k_1<>1 then begin

for j:=0 to st2 do

k2[j]:=k_1*kof2[j];

end;

end;

end;

for i:=1 to st1 do begin

k1[i-1]:=k1[i]-k2[i];

end;

st1:=st1-1;

until st1<st2;

if k1[0]<>0 then begin //Сокращение

sokr:=true;

for i:=1 to st1 do

if k1[i]<>0 then begin

if (k1[i] mod k1[0])<>0 then sokr:=false;

end;

k_1:=k1[0];

if sokr=true then

for i:=0 to st1 do

k1[i]:=k1[i] div k_1;

end;

for i:=0 to st2 do //Замена многочленов

k2_2[i]:=kof2[i];

for i:=0 to st1 do

k1_1[i]:=k1[i];

for i:=0 to 10 do begin

SGd3.Cells[i,0]:='';

SGd1.Cells[i,0]:='';

kof1[i]:=0;

k1[i]:=0;

kof2[i]:=0;

k2[i]:=0;

izub[n_iz,i]:=0;

end;

izubst[n_iz]:=st2;

for i:=0 to st2 do begin

k1[i]:=k2_2[i];

SGd1.Cells[i,0]:=inttostr(k1[i]);

izub[n_iz,i]:=k1[i];

if k1[i]<>0 then begin

//Edit4.Text:=Edit4.Text+IntToStr(k1[i])+'x^'+IntToStr(st2-i);

end;

if (k2_2[i+1]>0)and(i<st2) then //Edit4.Text:=Edit4.Text+'+';

end;

for i:=0 to st1 do begin

k2[i]:=k1_1[i];

kof2[i]:=k1_1[i];

end;

st3:=st1;

st1:=st2;

st2:=st3;

end;

until (st1=0);

d_st:=StrToInt(Edit1.Text);

for i:=d_st+1 downto 1 do begin

kof1[i]:=StrToInt(SGd4.Cells[d_st-(i-1),0]);

end;

//Нахождение Е

first:=true;

for n_nod:=1 to n_iz do begin

n:=d_st;

m:=izubst[n_nod];

d_st:=m;

for i:=n+1 downto 1 do begin

a[i]:=kof1[i];

end;

for i:=m+1 downto 1 do begin

b[i]:=izub[n_nod,m-(i-1)];

kof1[i]:=b[i];

end;

s:='f1(x)=';

for i:=n+1 downto 1 do begin

if a[i]<>0 then begin

if(a[i-1]<0)or(i=1) then begin

str(a[i],d);

str(i-1,k);

s:=s+d+'x^'+k;

end

else begin

str(a[i],d);

str(i-1,k);

s:=s+d+'x^'+k+'+';

end;

end;

end;

//Edit3.Text:=s;

s:='f2(x)=';

for i:=m+1 downto 1 do begin

if b[i]<>0 then begin

if(b[i-1]<0)or(i=1) then begin

str(b[i],d);

str(i-1,k);

s:=s+d+'x^'+k;

end

else begin

str(b[i],d);

str(i-1,k);

s:=s+d+'x^'+k+'+';

end;

end;

end;

//Edit4.Text:=s;

for j:=n+1 downto 1 do begin

a2[j]:=a[j];

b2[j]:=0;

end;

step:=n-m;

f:=n+2;

for i:=step+1 downto 1 do begin

f:=f-1;

buf[i]:=a2[f];

for j:=m+1 downto 1 do begin

b2[j]:=buf[i]*b[j];

end;

for j:=f downto 1 do begin

a2[j]:=a2[j]*b[m+1];

end;

for j:=f downto 1 do begin

a2[j]:=a2[j]-b2[j+1-i];

b2[j]:=0;

end;

end;

s:='h(x)=';

for i:=f+1 downto 1 do begin

e[n_nod,i]:=buf[i];

if buf[i]<>0 then begin

if(buf[i-1]<0)or(i=1) then begin

str(buf[i],d);

str(i-1,k);

s:=s+d+'x^'+k;

end

else begin

str(buf[i],d);

str(i-1,k);

s:=s+d+'x^'+k+'+';

end;

buf[i]:=0;

end;

end;

est[n_nod]:=f;

//Edit5.Text:=s;

s:='r(x)=';

for i:=n downto 0 do begin

if a2[i]<>0 then begin

if(a2[i-1]<0)or(i=1) then begin

str(a2[i],d);

str(i-1,k);

s:=s+d+'x^'+k;

end

else begin

str(a2[i],d);

str(i-1,k);

s:=s+d+'x^'+k+'+';

end;

end;

end;

Edit6.Text:=s;

first:=false;

end;

for n_nod:=1 to n_iz-1 do begin

n:=est[n_nod];

m:=est[n_nod+1];

d_st:=m;

for i:=n+1 downto 1 do begin

a[i]:=e[n_nod,i];

end;

for i:=m+1 downto 1 do begin

b[i]:=e[n_nod+1,i];

kof1[i]:=b[i];

if n_nod=n_iz-1 then fx[n_iz,i]:=b[i];

end;

s:='f1(x)=';

for i:=n+1 downto 1 do begin

if a[i]<>0 then begin if(a[i-1]<0)or(i=1) then begin

str(a[i],d);

str(i-1,k);

s:=s+d+'x^'+k;

end

else begin

str(a[i],d);

str(i-1,k);

s:=s+d+'x^'+k+'+';

end;

end;

end;

//Edit3.Text:=s;

s:='f2(x)=';

for i:=m+1 downto 1 do begin

if b[i]<>0 then begin if(b[i-1]<0)or(i=1) then begin

str(b[i],d);

str(i-1,k);

s:=s+d+'x^'+k;

end

else begin

str(b[i],d);

str(i-1,k);

s:=s+d+'x^'+k+'+';

end;

end;

end;

//Edit4.Text:=s;

for j:=n+1 downto 1 do begin

a2[j]:=a[j];

b2[j]:=0;

end;

step:=n-m;

f:=n+2;

for i:=step+1 downto 1 do begin

f:=f-1;

buf[i]:=a2[f];

for j:=m+1 downto 1 do begin

b2[j]:=buf[i]*b[j];

end;

for j:=f downto 1 do begin

a2[j]:=a2[j]*b[m+1];

end;

for j:=f downto 1 do begin

a2[j]:=a2[j]-b2[j+1-i];

b2[j]:=0;

end;

end;

s:='h(x)=';

for i:=f+1 downto 1 do begin

fx[n_nod,i]:=buf[i];

if buf[i]<>0 then begin if(buf[i-1]<0)or(i=1) then begin

str(buf[i],d);

str(i-1,k);

s:=s+d+'x^'+k;

end

else begin

str(buf[i],d);

str(i-1,k);

s:=s+d+'x^'+k+'+';

 end;

buf[i]:=0;

end;

end;

//Edit5.Text:=s;

fxst[n_nod]:=f;

s:='r(x)=';

for i:=n downto 0 do begin

if a2[i]<>0 then begin if(a2[i-1]<0)or(i=1) then begin

str(a2[i],d);

str(i-1,k);

s:=s+d+'x^'+k;

end

else begin

str(a2[i],d);

str(i-1,k);

s:=s+d+'x^'+k+'+';

end;

end;

end;

Edit6.Text:=s;

end;

fxst[n_iz]:=est[n_iz]+1;

Edit6.Text:='';

s:='';

for i:=1 to n_iz do begin

s:=s+'(';

for j:=fxst[i] downto 0 do begin

if fx[i,j]<>0 then begin

if(fx[i,j-1]<0)or(j=1) then begin

str(fx[i,j],d);

str(j-1,k);

s:=s+d+'x^'+k;

end

else begin

str(fx[i,j],d);

str(j-1,k);

s:=s+d+'x^'+k+'+';

end;

end;

end;

s:=s+')^'+IntToStr(i)+' ';

Edit6.Text:=Edit6.Text+s;

s:='';

end;

for i:=0 to 10 do begin

SGd1.Cells[i,0]:=SGd4.Cells[i,0];

end;

end;

end.

Заключение

При выполнении дипломной работы я рассмотрела следующие вопросы:

– делимость многочленов;

– деление многочленов с остатком;

– наибольший общий делитель, алгоритм Евклида;

– кратные корни;

– кратные множители, выделение кратных множителей;

– производные от многочленов.

Составила программы для нахождения частного и остатка при делении многочленов; наибольшего общего делителя двух многочленов; производной многочлена.

Список использованной литературы

1.         Алгебра и теория чисел. Под ред. Н. Я. Виленкина. Москва: Просвещение, 1984.

2.         Архангельский А. Я. Программирование в Delphi 6. Москва: ЗАО Бином, 2003.

3.         Архангельский А. Я. Delphi 7. Справочное пособие. Москва: ООО Бином-Пресс, 2004.

4.         Курош А. Г. Курс высшей алгебры. Москва: Наука, 1971.

5.         Ляпин Е. С., Евсеев А. Е. Алгебра и теория чисел. Часть II. Линейная алгебра и полиномы. Москва: Просвещение, 1978.

6.         Мантуров О. В. и др. Математика в понятиях, определениях и терминах. Часть 2. Москва: Просвещение, 1982.

7.         Попов В.Б. Turbo Pascal. Москва: Финансы и статистика, 2000.

8.         Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. Москва: Наука, 1980.

9.         Сабинина Л. В. Математика в понятиях, определениях и терминах. Часть I. Москва: Просвещение, 1978.

10.       Сборник задач по алгебре. Под ред. А. И. Кострикина. Москва: Наука, 1987.

11.       Смолин Ю. Н. Алгебра и теория чисел. Перемь:1996.

12.       Солодовников А. С., Родина М. А. Задачник-практикум по алгебре. Часть IV. Москва: Просвещение, 1985.

13.       Фадеев Д. К. Лекции по алгебре. Москва: Наука, 1984.

14.       Фадеев Д. К., Соминский И. С. Сборник задач по высшей алгебре. Москва: Наука, 1968.

15.        Шварцбурд С. И. Избранные вопросы математики. Москва: Просвещение, 1980.