Навигация
Обчислення інтегралів найпростішим методом Монте-Карло
25792
знака
0
таблиц
3
изображения
10.4. Обчислення інтегралів найпростішим методом Монте-Карло.
а) nS - число точок, для яких 
, 
- загальне число точок. Рівномірно розігруємо точки (xi, yi)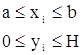 
, оцінка інтегралу є:
б) Ймовірнісна інтерпретація 
. Інтеграл - середнє значення функції, помножене на відрізок інтегрування. Розігруються, рівномірно, значення хі і розраховується значення f(xi).
10.5. Обчислення багатовимірних інтегралів методом Монте-Карло.
Для прикладу знайдемо центр мас і момент інерції двовимірного тіла:
Межі інтегрування визначаються геометрією тіла. Координати центра мас:
, 
.
Момент інерції навколо осі z:
.
Чисельна оцінка:
n - число точок, для яких 
- незалежні випадкові числа на відрізках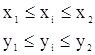 
і такі, що попадають у границі фігури.
Якщо для d = 1 - похибка апроксимації спадає, як n-a , то в d - вимірному випадку ця похибка спадає як n-a/d.
10.6. Аналіз похибки метода Монте-Карло.
Точність визначається кількістю випробувань в методі Монте-Карло або кількістю відрізків у класичних методах.
Для методу Монте-Карло похибка прямує до нуля, як 
.
Дисперсія є мірою похибки:
- дисперсія одиничного виміру,
, 
, 
,
, 
.
Якщо б 
не залежала від х, то 
.
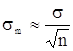- дисперсія середнього.
Похибку можна зробити малою, збільшуючи число випробувань або збільшуючи ефективність випробувань.
10.7. Нерівномірний розподіл ймовірності.
Побачили, як можна рівномірний розподіл використовувати для оцінки інтеграла.
Однак, важливо вибірку підінтегральної функції частіше виконувати, у областях 
, де 
велика або швидко змінюється. Для такої вибірки потрібен нерівномірний розподіл ймовірності. Розглянемо метод оберненого перетворення.
Введемо поняття щільності ймовірності p(x), при цьому 
- ймовірність того, що випадкове число належить відрізку 
.
нормується так, щоб
.
Нехай r – випадкове число, рівномірно розподілене на одиничному інтервалі [0,1] з густиною ймовірності:
.
Наше завдання знайти зв’язок між x i r, такий, що якщо rрівномірно розподілено, то х за законом p(x). Зв’язок встановлюють через інтегральну функцію розподілу:
,
де Р(x) – інтегральна функція розподілу, яка рівна ймовірності одержання випадкового числа меншого за х.
Зв’язок має вигляд:
.
Випадкова величина P(x) розподілена рівномовірно.
.
Ймовірність знайти x в інтервалі 
, рівна dP(x).
Співвідношення між dP(x) і dx можна знайти
отже в межах 0
r1 маємо dP(x)=P(x) dx=Pu(r) dr
Бачимо, що х розподілено з бажаною густиною імовірності.
Приклади:
Згенеруємо рівномірно розподілені на [a, b] числа. Шукана густина
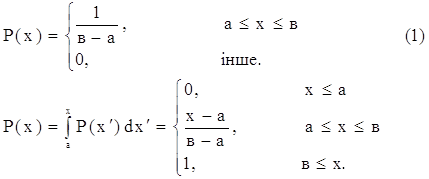
P(x) = r
x = P-1(r), 
, x= a + (в-a) r.
Змінна розподілена за законом (1), коли r—рівномовірне.
Інший випадок
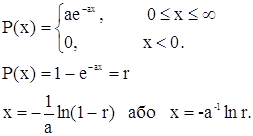
Однак метод оберненого перетворення може бути не найефективнішим. Для використання методу має виконуватись два співвідношення, має братись інтеграл Р(х) і розв’язуватись співвідношення Р(х)=r відносно х.
Для 
цього зробити не можна.
Однак можна згенерувати двовимірний гаусів розподіл
перейдемо до полярних координат.
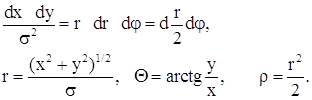
знайдемо імовірність у вигляді:
.
можемо генерувати розподілами за експоненційним законом, а 
рівномірно в межах [0,2
] то змінні 
будуть розподілені за нормальним законом з нульовим середнім і дисперсією 
.
10.8. Вибірка за значимістю (суттєва вибірка).
Похибка методу Монте-Карло пропорційна , познайомимось з методом зменшення . Введемо додатню Р(х) таку, що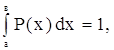 
тоді
можна переписати у такому виді
.
Обчислимо інтеграл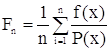 
, виконуючи вибірку у відповідності до розподілу Р(х), при рівномірному Р(х)=1/(в-а).
Вибираємо Р(х), що веде себе подібно до f(x) там де f(x) велика, тому підінтегральний вигляд буде функцією, що слабо змінюється і дисперсія буде малою.
10.9 Метод випадкового блукання (метод Метрополіса)
Метод одержання не рівномірного розподілу полягає у тому , що деякі вибірки відкладаються.
Нехай хочемо генерувати змінні з розподілом Р(х).
Випадкове блукання задається імовірністю переходу w(xi
xj) від одного xi до іншого xj для того, щоб розподіл точок x0, x1, x2,… сходився до Р(х).
Можна показати, що достатньо задовольняти умові детального балансу
Р(хі) w(xixj)=P(хj) w(xjxi),
де співвідношення не задає однозначного w(xjxi).
Розглянемо найпростіший варіант
w(xjxi) = min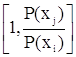
.
Перехід можна описати наступними кроками, нехай пішохід знаходиться в точці з координатою хn.
Для отримання хn+1:
Вибираємо пробну координату xt = хn + n.
Обчислюємо w =
Якщо w
1, приймаємо цей перехід і кладемо хn+1=xt.
Якщо w<1, генеруємо випадкове r.
Якщо rw, приймаємо цей перехід і кладемо хn+1=xt.
Якщо r>w, не приймаємо і хn+1=xn.
беруть таким, щоб приймалось від 1/3 до 1/2 кроків. Починають блукання з х для якого Р(х) максимальне.
Похожие работы
... ’язування задач у будь-якій галузі людської діяльності. Розв’язування задач у будь-якій галузі діяльності-це завжди одержання певних результатів обробки вхідних даних Для розв'язування задач комп'ютер озброєний найрізноманітнішими програмами, які поділяються на такі категорії: · операційні системи; · системи програмування; · прикладне програмне забезпечення. Оскі ...
... зичної освіти, а й важливий чинник загального розвитку школяра та професійного становлення у будь-якій галузі. Перша проблема, яку потрібно вирішити, упроваджую чи елементи комп'ютерного моделювання при вивченні фізики – вибір інструментальних засобів його реалізації. У час зародження сучасних інформаційних технологій єдиним способом було використання мов програмування високого рівня. За останні ...
... принтера також містить різні мови опису даних (Adobe PostScript, PCL і тощо.). Ці мови знову ж таки призначені для того, щоб забрати частину роботи у комп'ютера і передати її принтеру. Розглянемо фізичний принцип дії окремих компонентів лазерного принтера. 2.5.29 Фотобарабан Як вже писалося вище, найважливішим конструктивним елементом лазерного принтера є фотобарабан, що обертається, за ...
... , у принципі, здатний обробляти інформацію в 2L/L раз швидше в порівнянні зі своїм класичним аналогом. Звідси відразу видно, що маленькі квантові регістри (L<20) можуть служити лише для демонстрації окремих вузлів і принципів роботи квантового комп’ютера, але не принесуть великої практичної користі, тому що не зуміють обігнати сучасні ЕОМ, а коштувати будуть набагато дорожче. 1.3.Принципи ...
0 комментариев