Навигация
1. Декартовы координаты.
Пусть дан тройной интеграл от функции ![]()
![]()
причем область ![]() отнесена к системе декартовых координат Oxyz, Разобьем область интегрирования и плоскостями, параллельными координатным плоскостям. Тогда частичными областями будут параллелепипеды с гранями, параллельными плоскостям Оху, Охz, Оуz. Элемент объема .будет равен, произведению дифференциалов переменных интегрирования
отнесена к системе декартовых координат Oxyz, Разобьем область интегрирования и плоскостями, параллельными координатным плоскостям. Тогда частичными областями будут параллелепипеды с гранями, параллельными плоскостям Оху, Охz, Оуz. Элемент объема .будет равен, произведению дифференциалов переменных интегрирования
![]()
В соответствии с этим будем писать
![]()
Установим теперь правило для вычисления такого интеграла.
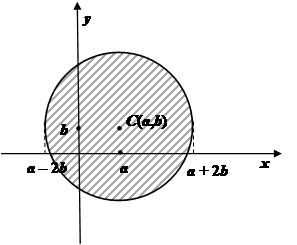
Будем считать, что область интегрирования ![]() имеет вид, изображенный на рис. 1).
имеет вид, изображенный на рис. 1).
Опишем около и цилиндрическую поверхность с образующей, перпендикулярной к плоскости Оху. Она касается области ![]() вдоль некоторой линии L, которая делит поверхность, ограничивающую область, на две части: верхнюю и нижнюю. Уравнением нижней поверхности пусть будет
вдоль некоторой линии L, которая делит поверхность, ограничивающую область, на две части: верхнюю и нижнюю. Уравнением нижней поверхности пусть будет ![]() , уравнением верхней
, уравнением верхней ![]() .
.
Построенная цилиндрическая поверхность высекает из плоскости Оху плоскую область D, которая является ортогональной проекцией пространственной области ![]() на плоскость Оху, при этом линия L проектируется в границу области
на плоскость Оху, при этом линия L проектируется в границу области ![]() .
.
Будем производить интегрирование сначала по Направлению оси Оz. Для этого функция ![]() интегрируется по заключенному в
интегрируется по заключенному в ![]() отрезку прямой, параллельной оси Оz и проходящей через некоторую точку Р(х, у) области D (на рис. 1 отрезок
отрезку прямой, параллельной оси Оz и проходящей через некоторую точку Р(х, у) области D (на рис. 1 отрезок ![]() ). При данных х и у переменная интегрирования z будет изменяться от
). При данных х и у переменная интегрирования z будет изменяться от ![]() - аппликаты точки “входа” (
- аппликаты точки “входа” (![]() ) прямой в область
) прямой в область ![]() , до
, до ![]() - аппликаты точки “выхода” (
- аппликаты точки “выхода” (![]() ) прямой из области
) прямой из области ![]() .
.
Результат интегрирования представляет собой величину, зависящую от точки Р (х, у); обозначим ее через F(х, у):
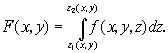
При интегрировании х и у рассматриваются здесь как постоянные.
Мы получим значение искомого тройного интеграла, если возьмем интеграл от функции F(х, у) при условии, что точка Р(х, у) изменяется по области D, т. е. если возьмем двойной интеграл
![]()
Таким образом, тройной интеграл I может быть представлен в виде
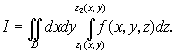
Приводя, далее, двойной интеграл по области D к повторному и интегрируя сначала по y, а затем по x, получим
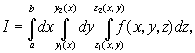 (*)
(*)
где ![]() и
и ![]() - ординаты точек “входа” в область D и “выхода” из нее прямой
- ординаты точек “входа” в область D и “выхода” из нее прямой ![]() (в плоскости Оху), а a и b - абсциссы конечных точек интервала оси Ох, на который проектируется область D.
(в плоскости Оху), а a и b - абсциссы конечных точек интервала оси Ох, на который проектируется область D.
Мы видим, что вычисление тройного интеграла по области ![]() производится, посредством трех последовательных интегрировании.
производится, посредством трех последовательных интегрировании.
Формула (*) сохраняется и для областей, имеющих цилиндрическую форму, т. е. ограниченных цилиндрической поверхностью с образующими, параллельными оси Оz, а снизу и сверху поверхностями, уравнения которых соответственно ![]() и
и ![]() (рис. 2).
(рис. 2).
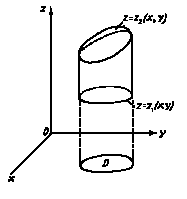
Рис.2
Если областью интегрирования служит внутренность параллелепипеда с гранями, параллельными координатным плоскостям (рис. 3), то пределы интегрирования постоянны во всех трех .интегралах :
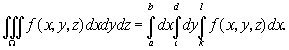
В этом случае интегрирование можно производить в любом порядке, пределы интегрирования будут при этом сохраняться.
Если же в общем случае менять порядок интегрирования ( т.е., скажем, интегрировать сначала по направлению оси Oy, а затем по области плоскости Oxz), то это приведёт к изменению порядка интегрирования в тройном интеграле и к изменению пределов интегрирования по каждой переменной.
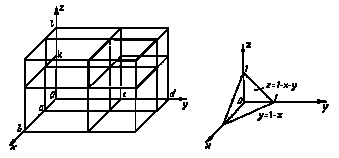
Рис.3 Рис.4
А) Пример.
Вычислим тройной интеграл
![]()
где ![]() - область, ограниченная координатными плоскостями
- область, ограниченная координатными плоскостями
![]()
и плоскостью ![]() (пирамида, изображённая на рис.4).
(пирамида, изображённая на рис.4).
Интегрирование по z совершается от z=0 до ![]() Поэтому, обозначая проекцию области
Поэтому, обозначая проекцию области ![]() на плоскость Oxy через D, получим
на плоскость Oxy через D, получим
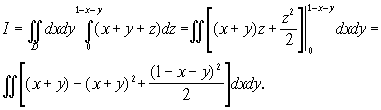
Расставим теперь пределы интегрирования по области D - треугольнику, уравнения сторон которого ![]()
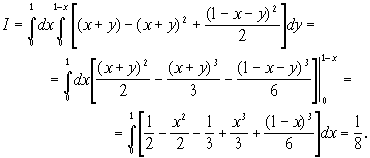
Похожие работы
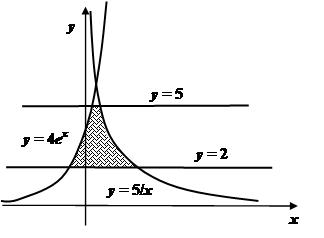
... так: , (10) где F1 и F2 – функции, полученные при подстановке в функцию f вместо x, y, z их выражений через цилиндрические (8) или сферические (9) координаты. 1.4 Геометрические и физические приложения кратных интегралов 1) Площадь плоской области S: (11) Пример 1. Найти площадь фигуры D, ограниченной линиями у = 2, у = 5. Решение. Эту площадь удобно вычислять, считая у ...
... выражения типа дивергенции по п- мерной области и интеграл по ограничивающей ее сверхповерхности S с уравнением L(x,y,z,…)=0. Если придерживаться прежних обозначений, то формула имеет вид (3) Впрочем, Остроградский не применял геометрических образов и терминов, которыми пользуемся мы: геометрия многомерных пространств в то время еще не существовала. В “Мемуаре об исчислении вариаций кратных ...
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... Из этой теоремы следует, что класс функций, представимых рядами Фурье, довольно широк. Поэтому ряды Фурье нашли широкое применение в различных отделах математики. Особенно успешно ряды Фурье применяются в математической физике и её приложениях к конкретным задачам механики и физики. Этот вопрос можно решить с помощью теоремы Дирихле. («Краткий курс высшей математики», Шнейдер и др., стр. 181) ...
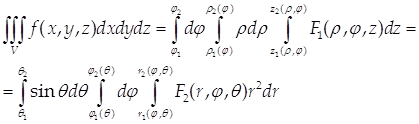


0 комментариев