Навигация
Условия оптимальности в задаче (3.2)
3.2 Условия оптимальности в задаче (3.2)
Условия оптимальности в задаче (3.2) представляют собой формулировку условий Куна-Таккера для этой задачи. Будем рассматривать следующую форму записи условий Куна-Таккера для задачи выпуклого программирования:
|
|
(3.2.1) |
В нашем случае получим:
|
|
(3.2.2) |
Здесь Ai- столбцы матрицы A длины m, Di столбцы матрицы D длины n, Lk - строки матрицы A длины n, ej - n-мерные столбцы единичной матрицы. Здесь и далее xi - компоненты оптимального вектора задачи x, l k и D k - множители Лагранжа условий Куна-Таккера. Запишем систему 3.2.2 в более обобщенной форме:
|
|
(3.2.3) |
где составные столбцы P0, ... Pm+2n каждый длиной m+n являются столбцами блочной матрицы P, имеющей следующий вид:
|
| (3.2.4) |
В таком виде условия Куна-Таккера (3.2.3) можно записать в еще более простом виде:
|
|
(3.2.5) |
Поскольку рассматриваемая нами задача является задачей выпуклого программирования, указанные условия существования минимума являются одновременно необходимыми и достаточными. Доказательство указанных условий можно найти в [1,2].
3.3. Базис задачи квадратичного программирования. Оптимальный и невырожденный базисы.
Поскольку ранг матрицы A равен m (см 3.1), система векторов
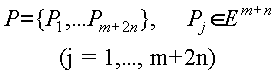
являются линейно независимой системой векторов. В то же время, легко видно, что линейная оболочка, натянутая на систему векторов P совпадает с пространством Em+n, т.е L(P)=En+m.
Следовательно из системы векторов 3.2.4 можно образовать конечное число базисов N евклидова пространства En+m, содержащих в себе векторы P1, .. Pm. Такие базисы пространства En+m будем называть базисами задачи квадратичного программирования, и обозначать следующим образом:
|
| (3.3.1) |
Для упрощения схемы алгоритма, запишем базис (3.3.1) в следующем виде:
|
| (3.3.2) |
Здесь Á 1 и Á 2 - наборы индексов. В случае, если Á 1=Á 2 будем считать базис UÁ 1,Á 2 порожденным одним множеством индексов Á =Á 1.
|
| (3.3.3) |
Коэффициенты разложения вектора b по базису UÁ 1,Á 2 будем называть базисными переменными, остальные коэффициенты - небазисными переменными.
Базис UÁ 1,Á 2 назовем оптимальным, если его базисные переменные удовлетворяют условиям Куна-Таккера (3.2.3).
Базис называется невырожденным, если все его базисные переменные, соответствующие компонентам вектора x отличны от нуля, т.е.
|
|
(3.3.4) |
Задачу (3.1.2) будем называть невырожденной, если все ее базисы невырождены. В противном случае назовем задачу вырожденной.
3.4. Метод субоптимизации на многообразиях. Выпуклый случай.
Для решения задачи (3.1.2) предлагается использовать метод
субоптимизации на многообразиях. Вначале рассмотрим основные идеи, приводящие к методу субоптимизации в случае задачи выпуклого программирования общего вида.
Рассмотрим задачу выпуклого программирования с линейными ограничениями, состоящую в минимизации выпуклой функции f(x) на множестве L, задаваемом ограничениями типа равенств.
|
| (3.4.1) |
Предположим, что задача имеет единственное решение, т.е минимум целевой функции достигается в единственной оптимальной точке x*. В этом случае задаче (3.4.1) эквивалентна задача:
|
|
(3.4.2) |
Эквивалентность этих двух задач является следствием единственности решения. Переход к задаче (3.4.2) называется выделением активных ограничений, т.е. вместо условия неотрицательности всех переменных, мы переходим к условию равенства нулю всех компонент, решения, индексы которых не принадлежат множеству Á (x*).
Предположим, что для задачи (3.4.2) нахождение оптимального решения существенно проще, чем для исходной задачи (3.4.1). В этом случае, перебирая каким-либо образом всевозможные множества индексов Á k, являющиеся подмножествами полного набора индексов {1,..n}, и решая для каждого из них задачу (3.4.2), используя Á k вместо Á *, определить искомое множество индексов Á *.
Предположим также, что задача (3.4.2) обладает свойством
единственности, т.е система векторов {L1, .. Lm, ej (jÎ Á (x*)}- линейно независима. В случае нарушения свойства единственности задача поиска оптимального вектора задачи (3.4.2) усложняется, и в дальнейшем этот случай рассматриваться не будет.
Алгоритм перебора множеств индексов Á k основан на следующей лемме.
Основная лемма:
Пусть x* является оптимальной точкой задачи:
|
| (3.4.3) |
где XÁ - линейное многообразие, определяемое следующим образом:
|
| (3.4.4) |
Предположим, что задача (3.4.3) с условием (3.4.4) обладает свойством единственности, и среди D j, удовлетворяющих условиям Куна-Таккера существует отрицательное D j0, т.е.
|
| (3.4.5) |
Пусть Á ' - множество индексов, полученное из Á вычитанием индекса j0:
|
| (3.4.6) |
Тогда, если x*' - оптимальный вектор задачи
|
| (3.4.7) |
то справедливо неравенство:
| f(x*')<f(x*) | (3.4.8) |
Доказательство.
Так как в силу выполнения соотношения (3.4.6) и определения множеств XÁ и XÁ ' вытекает, что XÁ ' É XÁ то имеет место неравенство f(x*') £ f(x*). Следовательно для доказательства соотношения (3.4.8) достаточно показать, что f(x*') ¹ f(x*).
Предположим, что это не так. Тогда точка x* является оптимальной для задач (3.4.3) и (3.4.7), и удовлетворяет условиям Куна-Таккера в обоих задачах:
|
| (3.4.9) |
|
| (3.4.10) |
Добавим в правую часть равенства (3.4.10) член 0ej0. Поскольку, по предположению (3.4.5) леммы коэффициент D j0 отличен от нуля, получаем разложение вектора градиента функции f по системе векторов {L1, .. Lm, ej (jÎ Á (x*)}. Получаем противоречие с условием единственности, а стало быть, и с условием основной леммы.
Доказанная лемма указывает направление перебора множеств индексов Á k (а стало быть и многообразий), уменьшающее значение целевой функции f(x).
Из доказанной леммы вытекает
Алгоритм поиска оптимального вектора
Общий вид алгоритма метода субоптимизации для задачи выпуклого программирования приведен на рис. 1. Ниже приводятся описания блоков алгоритма, изображенных на этом рисунке.
Блок 1. Определяется допустимая начальная точка x1 для исходной задачи. Это может быть точка, получаемая с помощью алгоритма построения начального базиса линейного симплекс-метода, или же решение в некотором смысле близкой линейной задачи. Предполагается Á 1=Á (x1), k=1.
Блок 2. Находится оптимальный вектор x*k для задачи
![]()
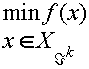
Если x*k оказывается допустимой для исходной задачи (3.4.1), совершается переход к блоку 3, в противном случае осуществляется переход к блоку 4.
Блок 3. Вычисляется значение
![]()
Если
![]()
то в силу выполнения условий Куна-Таккера для исходной задачи (3.4.1) точка x*k является оптимальной точкой задачи (3.4.1) и работа алгоритма заканчивается.
Если
![]()
то предполагаем
![]()
и происходит переход к блоку 2.
Блок 4. Поскольку оптимальная точка вспомогательной задачи оказалась недопустимой для исходной, выбираем в качестве новой начальной точки ближайшую к ней точку, допустимую для исходной задачи (3.4.1), и лежащую на прямой, соединяющей оптимальные точки вспомогательной задачи, т.е.
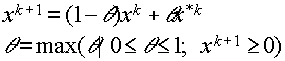
Далее полагаем Á k+1=Á (xk+1), заменяем k на k+1, и переходим к блоку 2.
Таким образом построен итерационный процесс, позволяющий осуществить направленный перебор множеств индексов Á k, позволяющий найти оптимальный вектор исходной задачи. Сходимость процедуры будет рассмотрена позже.
Похожие работы
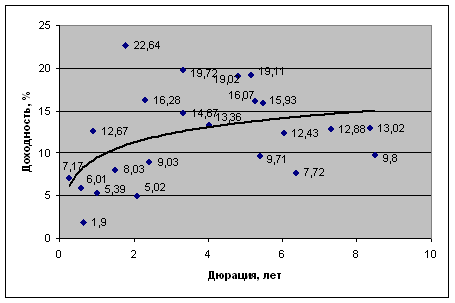
... негативных последствий для инвестиционного портфеля ОАО «МХК «ЕвроХим» и поиску путей формирования оптимальной структуры портфеля ценных бумаг организации на текущую дату. Рис. 4. Доходность еврооблигаций ОАО «МХК «ЕвроХим» на 02.03.2009 г. 3. Управление инвестиционным портфелем предприятия 3.1 Направления совершенствования структуры инвестиционного портфеля По сравнению с ...
... реализацию следующих этапов: Постановка целей и выбор адекватного типа портфеля. Анализ объектов инвестирования. Формирование инвестиционного портфеля. Выбор и реализация стратегии управления портфелем. Оценка эффективности принятых решений. Первый этап включает определение целей инвестирования, способных обеспечить их достижение портфелей и необходимого объема вкладываемых средств. Следует ...
... МТС-ао 271,43 276,85 234,35 161,82 Сбербанк 72,65 65,31 44,72 31,13 Уркалий-ао 328 249,08 165,88 122,01 ГМКНорНик 5 050,91 4 917 3 379,26 1 850,28 2. Формирование инвестиционного портфеля При формировании портфеля ценных бумаг учитывается уровень ожидаемой доходности и уровень риска той или иной ценной бумаги. При расчете текущей доходности мы используем следующую формулу: ...
... , портфель ценных бумаг является тем инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске. 3. ПРИНЦИПЫ ФОРМИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ При формировании инвестиционного портфеля следует руководствоваться следующими соображениями: безопасность вложений (неуязвимость инвестиций от потрясений на рынке инвестиционного капитала), ...
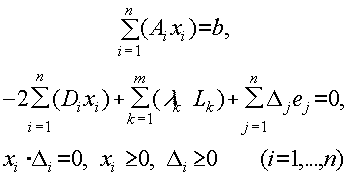
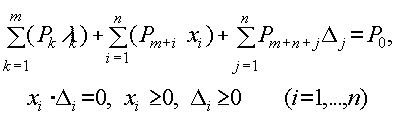
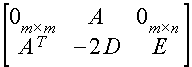
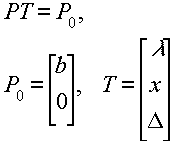
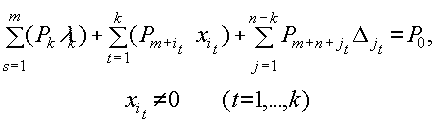
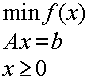
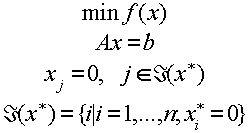
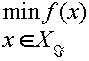
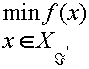
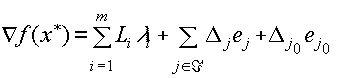
0 комментариев