Навигация
1. Новое Z уравнение.
старое Z уравнение : ( 1 -1 -25 0 0 0 )
( ( -25 ) * ( 0 -1/2 1 0 1/2 0 )
( 1 -131/2 0 0 121/2 0 )
Новое S1 уравнение
старое S1 уравнение : ( 0 5 100 1 0 1000 )
( 100 ) * ( 0 -1/2 1 0 1/2 0 )
( 0 55 0 1 -50 1000 )
Новая симплекс-таблица будет иметь вид :
| Базисные переменные | Z | X1 | X2 | S1 | S2 | Решение | |
| Z | 1 | -131/2 | 0 | 0 | 121/2 | 0 | Z – уравнение |
| S1 | 0 | 55 | 0 | 1 | -50 | 1000 | S1 –уравнение |
| X2 | 0 | -1/2 | 1 | 0 | 1/2 | 0 | X2 – уравнение |
В новом решении X1 = 0 и S2 = 0. Значение Z не изменяется.
Заметим, что новая симплекс-таблица обладает такими же характеристиками, как и предыдущая : только небазисные переменные X1 и S2 равны нулю, а значения базисных переменных, как и раньше, представлены в столбце « Решение ». Это в точности соответствует результатам, получаемым при использовании метода Гаусса—Жордана.
Из последней таблицы следует, что на очередной итерации в соответствии с условием оптимальности в качестве вводимой переменной следует выбрать X1, так как коэффициент при этой переменной в
Z-ypaвнении равен -131/2. Исходя из условия допустимости, определяем, что исключаемой переменной будет S1. Отношения, фигурирующие в правой части таблицы, показывают, что в новом базисном решении значение включаемой переменной X1 будет равно 1000/55 ( = минимальному отношению ). Это приводит к увеличению целевой функции на ( 1000/55 ) * ( -131/2 ) = ( 2455/11 ).
К получению симплекс-таблицы, соответствующей новой итерации, приводят следующие вычислительные операции метода Гаусса—Жордана.
Новое ведущее S1 уравнение = Предыдущее S1 уравнение / ( 55 ).
| Базисные переменные | Z | X1 | X2 | S1 | S2 | Решение |
| Z | ||||||
| S1 | 0 | 1 | 0 | 1/55 | 50/55 | 1000/55 |
| X2 |
2) Новое Z уравнение = Предыдущее Z уравнение ( -131/2 ) * Новое /ведущее уравнение :
( 1 -131/2 0 0 121/2 0 )
( -131/2 ) * ( 0 1 0 1/55 -50/55 1000/55 )
( 1 0 0 27/110 5/22 2455/11 )
3) Новое X2 уравнение = Предыдущее X2 уравнение ( -1/2 ) * Новое ведущее уравнение :
( 0 -1/2 1 0 1/2 0 )
( 1/2 ) * ( 0 1 0 1/55 -50/55 1000/55 )
( 0 0 1 1/110 1/22 91/11 )
В результате указанных преобразований получим следующую симплекс-таблицу.
| Базисные переменные | Z | X1 | X2 | S1 | S2 | Решение |
| Z | 1 | 0 | 0 | 27/110 | 5/22 | 2455/11 |
| X1 | 0 | 1 | 0 | 1/55 | -50/55 | 1000/55 |
| X2 | 0 | 0 | 1 | 1/110 | 1/22 | 91/11 |
В новом базисном решении X1=1000/55 и X2=91/11. Значение Z увеличилось с 0 ( предыдущая симплекс-таблица ) до 2455/11 ( последняя симплекс-таблица ). Этот результирующий прирост целевой функции обусловлен увеличением X1 от О до 1000/55, так как из Z строки предыдущей симплекс-таблицы следует, что возрастанию данной переменной на единицу соответствует увеличение целевой функции на( -131/2 ).
Последняя симплекс-таблица соответствует оптимальному решению задачи, так как в Z уравнении ни одна из небазисных переменных не фигурирует с отрицательным коэффициентом. Получением этой pезультирующей таблицы и завершаются вычислительные процедуры симплекс-метода.
В рассмотренном выше примере алгоритм симплекс-метода использован при решении задачи, в которой целевая функция подлежала максимизации. В случае минимизации целевой функции в этом алгоритме необходимо изменить только условие оптимальности : в качестве новой базисной переменнойследует выбирать ту переменную, которая в Z уравнении имеет наибольший положительный коэффициент. Условия допустимости в обоих случаях ( максимизации и минимизации ) одинаковы. Представляется целесообразным дать теперь окончательные формулировки обоим условиям, используемым в симплекс-методе.
Условие оптимальности. Вводимой переменной в задаче максимизации ( минимизации ) является небазисная переменная, имеющая в Z -уравнении наибольший отрицательный ( положительный ) коэффициент, В случае равенства таких коэффициентов для нескольких небазисных переменных выбор делается произвольно, если все коэффициенты при небазисных переменных в Z уравнении неотрицательны (неположительны), полученное решение является оптимальным.
Условие допустимости, в задачах максимизации и минимизации в качестве исключаемой переменной выбирается та базисная переменная, для которой отношение постоянной в правой части соответствующего ограничения к ( положительному ) коэффициенту ведущего столбца минимально. В случае равенства этого отношения для нескольких базисных переменных выбор делается произвольно.
Оптимальное решениеС точки зрения практического использования результатов решения задач ЛП классификация переменных, предусматривающая их разделение на базисные и небазнсные, не имеет значения и при анализе данных, характеризующих оптимальное решение, может не учитываться. Переменные, отсутствующие в столбце « Базисные переменные », обязательно имеют нулевое значение. Значения остальных переменных приводятся в столбце « Решение ». При интерпретации результатов оптимизации в нашей задаче нас прежде всего интересует количество времени, которое закажет наша фирма на радио и телевидение, т. е. значения управляемых переменных X1 и X2. Используя данные, содержащиеся в симплекс-таблице для оптимального решения, основные результаты можно представить в следующем виде :
| Управляемые переменные | Оптимальные значения | Решение |
| X1 | 1000/55 | Время выделяемое фирмой на телерекламу |
| X2 | 91/11 | Время выделяемое фирмой на радиорекламу |
| Z | 2455/11 | Прибыль получаемая от рекламы. |
Заметим, что Z = X1 + 25X2 = 1000/55 + 25 * 91/11 = 2455/11. Это решение соответствует данным заключительной симплекс-таблицы.
Статус ресурсовБудем относить ресурсы к дефицитным или недифицитным в зависимости от того, полное или частичное их использование предусматривает оптимальное решение задачи. Сейчас цель состоит в том, чтобы получить соответствующую информацию непосредственно из симплекс-таблицы для оптимального решения. Однако сначала следует четко уяснить следующее. Говоря о ресурсах, фигурирующих в задаче ЛП, мы подразумеваем, что установлены некоторые максимальные пределы их запасов, поэтому в соответствующих исходных ограничениях должен использоваться знак <=. Следовательно, ограничения со знаком => не могут рассматриваться как ограничения на ресурсы. Скорее, ограничения такого типа отражают то обстоятельство, что решение должно удовлетворять определенным требованиям, например обеспечению минимального спроса или минимальных отклонений от установленных структурных характеристик производства ( сбыта ).
В модели, построенной для нашей задачи, фигурирует ограничение со знаком <=. Это требование можно рассматривать как ограничение на соответствующий « ресурс », так как увеличение спроса на продукцию эквивалентно расширению « представительства » фирмы на рынке сбыта.
Из вышеизложенного следует, что статус ресурсов ( дефицитный или недефицитный ) для любой модели ЛП можно установить непосредственно из результирующей симплекс-таблицы, обращая внимание на значения остаточных переменных. Применительно к нашей задаче можно привести следующую сводку результатов :
| Ресурсы | Остаточная переменная | Статус ресурса |
| Ограничение по бюджету | S1 | Дефицитный |
| Превышение времени рекламы радио над теле | S2 | Дефицитный |
Положительное значение остаточной переменной указывает на неполное использование соответствующего ресурса, т. е. данный ресурс является недефицятным. Если же остаточная переменная равна нулю, это свидетельствует о полном потреблении соответствующего ресурса. Из таблицы видно, что наши ресурсы являются дефицитными. В случае недефицитности любое увиличение ресурсов сверх установленного максимального значения привело бы лишь к тому, что они стали бы еще более недефнинтными. Оптимальное решение задачи при этом осталось бы неизменным.
Ресурсы, увеличение запасов которых позволяет улучшить решение ( увеличить прибыль ), — это остаточные переменные S1 и S2, поскольку из симплекс-таблицы для оптимального решения видно, что они дефицитные. В связи с этим логично поставить следующий вопрос: какому из дефицитных ресурсов следует отдать предпочтение при вложении дополнительных средств на увеличение их запасов, с тем чтобы получить от них максимальную отдачу ? Ответ на этот вопрос будет дан в следующем подразделе этой главы, где рассматривается ценность различных ресурсов.
Ценность ресурсаЦенность ресурса характеризуется величиной улучшения оптимального значения Z, приходящегося на единицу прироста объема данного ресурса.
Информация для оптимального решения задачи представлена в симплекс-таблице. Обратим внимание на зн ачения коэффициентов Z уравнения, стоящих при перем енны х начальног о базиса S1 и S2. Выделим для удобства соответстзующую часть симп лекс-табли цы :
| Базисные переменные | Z | X1 | X2 | S1 | S2 | Решение |
| Z | 1 | 0 | 0 | 27/110 | 5/22 | 2455/11 |
Как следует и з теории решения задач Л П, цен ность ресурсов всегда можно опреде лить по значениям коэффициен тов п ри переменных начального бази са, фигурирующих в Z уравнении оптимальной симплекс-табли цы, таким образом Y1 = 27/110, а Y2 = 5/22.
Покажем, каким образом аналогичный результат можно получить непосредственно из симплекс-таблицы для оптимального решения . Рассмотрим Z уравнение симпле кс-таблицы для оптимального решения нашей задачи
Z = 2455/11 ( 27/110S1 + 5/22S2 ).
Положительное приращение переменной S1 относительно ее текущего нуле вого значения приводит к пропорциональному уменьшению Z, причем коэффи циент пропорциональности равен 27/110. Но, как следует из первого ограничения модели :
5X1 + 100X2 + S1 = 1000
увеличе ни е S1 эквивалентно снижению количества денег выделеных на рекламу ( далее мы будем использовать в тексте, как первый ресурс ). Отсюда следует, что уменьшение количества денег выделеных на рекламу вызывает пропорциональное уменьшение целевой функции с тем же коэффи циентом пропорциональности, равным 27/110. Так как мы оперируем с линейными функциями, полученный вывод можно обобщ ить, считая, что и увеличение количества денег выделеных на рекламу ( эквивалентное в веде нию и зб ыточной переме нной S1 < 0 ) приводит к пропорци ональному увеличению Z с тем же коэффициентом пропорциональности, равным 27/110. Аналогичные рассуждения справ едливы для ограничения 2.
Несмотря на то что ценность различных ресурсов, оп ределяема я значе ниями переменных Yi, была представлена в стоимостном выражении, ее нельзя отождествлять с действ ительными ценам и, по которым возможна закупка соотве тствующи х ресурсов. На самом де ле речь идет о некоторой мере, име ющей экономическую природу н количественно характеризующей ценность ресурса только относительно полученного оптимального значения целевой функции. При изменении ограничении модели соответствующие экономические оценки будут меняться даже тогда, когда оптимизируемый процесс предполагает применение тех же ресурсов. Поэтому при характеристике ценности ресурсов экономисты предпочитают использовать такие терминыт, как теневая цена, скрытая цена, или более специфичный термин — двойственная оценка.
Заметим, что теневая цена ( ценность ресурса ) характеризует интенсивность улучшения оптимального значения Z. Однако при этом не фиксируется интервал значений увеличения запасов ресурса, при которых интенсивность улучшения целевой функции остается постоянной. Для большинства практических ситуаций логично предположить наличие верхнего предела увеличения запасов, при превышении которого соответствующее ограничение становится избыточным, что в свою очередь приводит к новому базисному решению и соответствующим ему новым теневым ценам. Ниже определяется нитервал значений запасов ресурса, при которых соответствующее ограничение не становится избыточным.
Максимальное изменение запаса ресурсаПри решении вопроса о том, запас какого из ресурсов следует увеличивать в первую очередь, обычно используются теневые цены Чтобы определить интервал значений изменения запаса ресурса, при которых теневая цена данного ресурса, ( фигурирующая в заключительной симплекс-таблице, остается неизменной, необходимо выполнить ряд дополнительных вычислений. Рассмотрим сначала соответствующие вычислительные процедуры, а затем покажем, как требуемая информация может быть получена из симплекс-таблицы для оптимального решения.
В нашей задаче запас первого ресурса изменился на т. е. запас бюджета составит 1000 + . При положительной величине запас данного ресурса увеличивается, при отрицательной — уменьшается. Как правило, исследуется ситуация, когда объем ресурса увеличивается ( > 0 ), однако, чтобы получить результат в общем виде, рассмотрим оба случая.
Как изменится симплекс-таблица при изменении величины запаса ресурса на? Проще всего получить ответ на этот вопрос. если ввести в правую часть первого ограничения начальной симплекс-таблицы и затем выполнить все алгебраические преобразования, соответствующие последовательности итераций. Поскольку правые части ограничений никогда не используются в качестве ведущих элементов, то очевидно, что на каждой итерации будет оказывать влияние только на правые части ограничений.
| Уравнение | Значения элементов правой части на соответствующих итерациях | ||
| ( начало вычислений ) | 1 | 2 ( оптимум ) | |
| Z | 0 | 0 | 2455/11 |
| 1 | 1000 | 1000 + | 1000/55 + |
| 2 | 0 | 0 | 91/11 |
Фактически вce изменения правых частей ограничений, обусловленные введением , можно определить непосредственно по данным, содержащимся в симплекс-таблицах. Прежде всего заметим, что на каждой итерации новая правая часть каждого ограничения представляет собой сумму двух величин: 1) постоянной и 2) члена, линейно зависящего от . Постоянные соответствуют числам, которые фигурируют на соответствующих итерациях в правых частях ограничений симплекс-таблиц до введения . Коэффициенты при во вторых слагаемых равны коэффициентам при S1 на той же итерации. Так, например, на последнеи итерации ( оптимальное решение ) постоянные ( 2455/11 ; 1000/55 ; 91/11 ) представляют собои числа, фигурирующие в правых частях ограничении оптимальной симплекс-таблицы до введенияКоэффициенты ( 27/110 ; 1/55 ; 1/110 ) равны коэффициентам при S1 в той же симплекс-таблице потому, что эта переменная связана только с первым ограничением. Другими словами, при анализе влияния изменений в правой части второго ограничения нужно пользоваться коэффициентами при переменной S2.
Какие выводы можно сделать из полученных результатов? Так как введение сказывается лишь на правой части симплекстаблицы, изменение запаса ресурса может повлиять только на допустимость решения. Поэтому не может принимать значений, при которых какая-либо из ( базисных ) переменных становится отрицательной. Из этого следует, что величина должна быть ограничена таким интервалом значений, при которых выполняется условие неотрицательности правых частей ограничений в результирующей симплекс-таблице, т. е.
X1 = 1000/55 + ( 1/55 )> 0 ( 1 )
X2 = 91/11 + ( 1/110 )=> 0 ( 2 )
Для определения допустимого интервала изменения рассмотрим два случая.
Случай 1: > 0 Очевидно, что оба неравнества при этом условии всегда будут неотрицательными.
Случай 2: < 0. Решаем неравенства : ( 1 )
( 1/55 )=> 1000/55. Из этого следует, что => 1000
( 2 )
( 1/110 )=> 91/11. Из этого следует, что => 1000
Объединяя результаты, полученные для обоих случаев, можно сделать вывод, что при 1000 <= <= + решение рассматриваемой задачи всегда будет допустимым, любое значение , выходящее за пределы указанного интервала, приведет к недопустимости решения и новой совокупности базисных переменных.
Теперь рассмотрим в каких пределах может изменяться запас ресурса 2 анализ проведем по аналогичной схеме :
Запас 2-ого ресурса изменился на т. е. запас рекламного времени составит 0 + Как изменилась симплекс-таблица при изменении величины запаса ресурса напроиллюстрировано ниже.
| Уравнение | Значения элементов правой части на соответствующих итерациях | ||
| ( начало вычислений ) | 1 | 2 ( оптимум ) | |
| Z | 0 | 0 | 2455/11 |
| 1 | 1000 | 1000 | 1000/55 |
| 2 | 0 | 0 + | 91/11 + |
Найдем интервал ограничивающий величину
X1 = 1000/55 ( 50/55 )
X2 = 91/11 + ( 1/22 )
Для определения допустимого интервала изменения рассмотрим два случая.
Случай 1: > 0 Решаем неравенства : ( 1 )
( 50/55 )1000/55 из этого неравенства следует, что
Очевидно, что 2-ое уравнение неотрицательно на данном участке.
Объединяя 2 уравнения для Случая 1 мы получим интервал для
[ 0 ; 20 ]
Случай 2: < 0. Решаем неравенства : ( 1 )
( 50/55 )1000/55. Из этого следует, что 20
( 2 )
( 1/22 )91/11. Из этого следует, что
Объединяя 2 уравнения для Случая 2 мы получим интервал для
[ 200 ; 0 ]
Объединяя 2 случая мы получим интервал [ 200 ; 20 ]
Максимальное изменение коэффициентов удельной прибыли ( стоимости )
Наряду с определением допустимых изменений запасов ресурсов представляет интерес и установление интервала допустимых изменений коэффициентов удельной прибыли ( или стоимости ). Следует отметить, что уравнение целевой функции никогда не используется в качестве ведущего уравнения. Поэтому любые изменения коэффициентов целевой функции окажут влияние только на Z-уравнение результирующей симплекс-таблицы. Это означает, что такие изменения могут сделать полученное решение неоптимальным. Наша цель заключается в том, чтобы найти интервалы значений изменений коэффициентов целевой функции ( рассматривая каждый и з коэффициентов отдельно ), п ри которых оптимальные значе ни я переменных остаются неизме нными.
Чтобы пок азать , как выполняются соответствующие вычислен ия, положим, что удельный объем сбыта, ассоциированной с пере менной
X1 изменяется от 1 до 1 + где может быть как положительным, так и отрицательным числом. Целевая функция в этом случае принимает следующий вид:
Z = ( 1 + X1 + 25X2
Если воспользоваться данными начальной симплекс-таблицы и выполнить все вычисления, необходимые для ( получения заключнтельной симплекс-таблицы, то последнее Z-уравнение будет выглядеть следующим образом:
| Базисные переменные | X1 | X2 | S1 | S2 | Решение |
| Z | 0 | 0 | 27/110+1/55 | 5/22-50/55 | 2455/11+1000/55 |
Коэффициенты при базисных переменных X1, X2 и остаточных я равными нулю. Это уравнение отличается от Z-уравнения до введения, только наличием членов, содержащих . Коэффициенты при равны кoэффициентам при соответствующих переменных в Z-уравнении симплекс-таблицы для полученного ранее оптимального решения
| Базисные переменные | X1 | X2 | S1 | S2 | Решение |
| X1 | 1 | 0 | 1/55 | -50/55 | 1000/55 |
Мы рассматриваем X1 уравнение, так как коэффициент именно при этон переменной в выражении для целевои функции изменился на.
Оптимальные значения переменных будут оставаться неизменными при значениях , удовлетворяющих условию неотрицательности ( задача на отыскание максимума ) всех коэффициентов при небазисных переменных в Z-уравнении. Таким образом, должны выполняться следующие неравенства :
27/110 + 1/55
5/22 50/55
Из первого неравенства получаем, что => 13,5, а из второго следует что <= 1/4. Эти результаты определяют пределы изменения коэффициента C1 в виде следующего соотношения : 13,5 <= <= 1/4. Таким образом, при уменьшении коэффициента целевой функции при переменной X1 до значения, равного 1 + ( 13,5 ) = 12,5 или при его увеличении до 1 + 13,5 = 14,5 оптимальные значения переменных остаются неизменными. Однако оптимальное значение Z будет изменяться ( в соответствии с выражением 2455/11 + 1000/55, где 13,5 <= <= 1/4
X2 изменяется от 25 до 25 + где может быть как положительным, так и отрицательным числом. Целевая функция в этом случае принимает следующий вид:
Z = ( 25 + X2 + X1
Все предыдущее обсуждение касалось исследования изменения коэффициента при переменной, которой поставлено в соответствие ограничение, фигурирующее в симплекс-таблице. Однако такое ограничение имеется лишь в том случае, когда данная переменная является базисной ( например X1 и X2 ). Если переменная небазисная, то в столбце, содержащем базисные переменные, она не будет представлена.
Любое изменение коэффициента целевой функции при небазисной переменной приводит лишь к тому, что в заключительной симплкс-таблице изменяется только этот коэффициент. Рассмотрим в качестве иллюстрации случай, когда коэффициент при переменной S1 ( первой остаточной переменной ) изменяется от 0 до Выполнение преобразований, необходимых для получения заключительной симплекс таблицы, приводит к следующему результирующему Z-уравнению :
| Базисные переменные | X1 | X2 | S1 | S2 | Решение |
| Z | 0 | 0 | 27/110+1/55 | 5/22 | 2455/11 |
Похожие работы
... определение базисных решений соответст- вует идентификации экстремальных точек , осуществляемой при геометрическом представлении пространства решений . Таким об- разом , максимальное число итераций при использовании симплекс- метода равно максимальному числу базисных решений задачи ЛП , представленной в стандартной форме . Это означает , что количество итерационных процедур симплекс-метода не ...
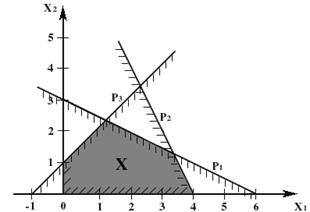
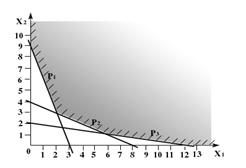
... ограничения несовместны, множество планов пусто и задача ЛП решения не имеет. Рис. 1.4 Рис. 1.5 Рис. 1.6 2. Симплекс-метод 2.1 Идея симплекс-метода Рассмотрим универсальный метод решения канонической задачи линейного программирования , , , с n переменными и m ограничениями-равенствами, известный как симплекс-метод. Множество планов канонической задачи – ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... на t3 часов. Прибыль от реализации единицы готового изделия А составляет a рублей, а изделия В - b рублей. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу простым симплекс-методом. Дать геометрическое истолкование задачи, используя для этого её формулировку с ограничениями-неравенствами. а1 = 1 b1 = 5 t1 = 10 a = 2 а2 = 3 b2 = 2 t2 ...


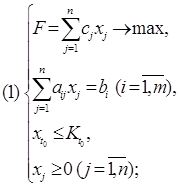
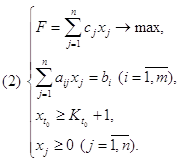
0 комментариев