Навигация
3. Если
![]()
то
![]() . (5)
. (5)
Равенства (4) и (5) доказываются дифференцированием правой и левой частей равенств.
Пример 1.
![]()
=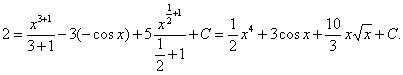
Пример 2.
![]()
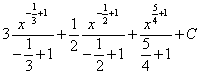 =
=
=![]()
Пример 3.
![]() .
.
Пример 4.
![]()
Пример 5.
![]()
4)Интегрирование методом замены переменой или способом подстановки
Пусть требуется найти интеграл ![]() , причем непосредственно подобрать первообразную для f(x) мы не сможем , но нам известно, что она существует.
, причем непосредственно подобрать первообразную для f(x) мы не сможем , но нам известно, что она существует.
Сделаем замену переменной в подынтегральном выражении, положив
x=φ(t), (1)
где φ(t)-непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда dx= φ′(t)dt;докажем, что в этом случае имеет место следующее равенство:
![]() (2)
(2)
Здесь подразумевается, что после интегрирования в правой части равенства вместо t будет подставлено его выражение через х на основании равенства (1).
Для того чтобы установить, что выражения, стоящие справа и слева, одинаковы в указанном выше смысле, нужно доказать, что их производные по х равны между собой . Находим производную от левой части : ![]() Правую часть равенства (2) будем дифференцировать по х как сложную функцию, где t-промежуточный аргумент. Зависимость t от х выражается равенством (1), при этом
Правую часть равенства (2) будем дифференцировать по х как сложную функцию, где t-промежуточный аргумент. Зависимость t от х выражается равенством (1), при этом ![]() и по правилу дифференцирования обратной функции
и по правилу дифференцирования обратной функции ![]() .
.
Таким образом, имеем
![]()
Следовательно, производные от х от право й и левой частей равенства (2) равны, что и требовалось доказать.
Функцию ![]() следует выбирать так, чтобы можно было вычислить неопределенный интеграл, стоящий в правой части равенства (2).
следует выбирать так, чтобы можно было вычислить неопределенный интеграл, стоящий в правой части равенства (2).
Замечание. При интегрировании иногда целесообразнее подбирать замену переменной не в виде ![]() , а в виде
, а в виде ![]() Проиллюстрируем это на примере. Пусть нужно вычислить интеграл, имеющий вид
Проиллюстрируем это на примере. Пусть нужно вычислить интеграл, имеющий вид
![]() .
.
Здесь удобно положить
![]() ,
,
тогда ![]()
![]() .
.
Приведем несколько примеров на интегрирование с помощью замены переменных.
Пример 1.
![]() Сделаем подстановку t=sin x; тогда dt= cosx dx и, следовательно,
Сделаем подстановку t=sin x; тогда dt= cosx dx и, следовательно,
![]()
Пример 2.
![]() Полагаем t=1+x2 ;тогда dt=2xdx и
Полагаем t=1+x2 ;тогда dt=2xdx и
![]()
Пример 3.
![]() Полагаем
Полагаем ![]() ; тогда dx=a dt,
; тогда dx=a dt,
![]()
Пример 4. ![]() . Полагаем
. Полагаем ![]() ; тогда dx=a dt,
; тогда dx=a dt,
![]()
(предполагается, что a>0).
В примерах 3 и 4 выделены формулы ,приведенные в таблице интегралов под номерами 11′и 13′(см. выше,пункт №2).
Пример 5. ![]() Полагаем t=lnx; тогда
Полагаем t=lnx; тогда ![]()
![]() .
.
Пример 6. ![]() ? Полагаем
? Полагаем ![]() ;тогда dt= 2xdx,
;тогда dt= 2xdx,
![]()
Метод замены переменных является одним из основных методов вычисления неопределенных интегралов. Даже в тех случаях, когда мы интегрируем каким -либо другим методом, нам часто приходится в промежуточных вычислениях прибегать к замене переменных. Успех интегрирования зависит в значительной степени от того, сумеем ли мы подобрать такую удачную замену переменных, которая упростила бы данный интеграл. По существу говоря изучение методов интегрирования сводится к выяснению того, какую надо сделать замену переменной при том или ином виде подынтегрального выражения. Этому посвящены большая часть настоящего пункта.
5)Интегрирование по частям
Пусть u и v две дифференцируемые функции от х. Тогда, как известно, дифференциал произведения uv вычисляется по следующей формуле :d(uv)=udv+vdu.Отсюда, интегрируя, получаем ![]() или
или
![]() . (1)
. (1)
Последняя формула называется формула интегрирования по частям. Эта формула чаще всего применяется к интегрированию выражений которые можно так представить в виде произведения двух сомножителей u и dv, чтобы отыскать функцию v по её дифференциалу dv и вычисления интеграла ![]() составляли в совокупности задачу более простую, чем непосредственное вычисление интеграла
составляли в совокупности задачу более простую, чем непосредственное вычисление интеграла![]() . Умение разбивать разумным образом данное подынтегральное выражение на множители u и dv вырабатывается в процессе решения задачи , и мы покажем на ряде примеров, как это делается.
. Умение разбивать разумным образом данное подынтегральное выражение на множители u и dv вырабатывается в процессе решения задачи , и мы покажем на ряде примеров, как это делается.
Пример 1. ![]() ? Положим u=x,dv=sinxdx;тогда du=dx,v= -cosx.Следовательно,
? Положим u=x,dv=sinxdx;тогда du=dx,v= -cosx.Следовательно,
![]() .
.
Замечание. При определении функции v по дифференциалу dv мы можем брать любую произвольную постоянную, так как в конечный результат она не входит (что легко проверить, подставив в равенство(1) вместо v выражение v+C). Поэтому удобно считать эту постоянную равной нулю.
Правило интегрирования по частям применяется во многих случаях. Так, например, интегралы вида
![]()
некоторые интегралы, содержащие обратные тригонометрические функции, вычисляются с помощью интегрирования по частям.
Пример 2. Требуется вычислить ![]() . Положим u= arctg x, dv=dx;тогда
. Положим u= arctg x, dv=dx;тогда ![]() . Следовательно,
. Следовательно,
![]()
Пример 3. Требуется вычислить ![]() . Положим
. Положим ![]() тогда
тогда ![]()
![]() .
.
Последний интеграл снова интегрируем по частям, полагая
![]() Тогда
Тогда
![]() . Окончательно будем иметь
. Окончательно будем иметь
![]() .
.
Рациональные дроби. Простейшие рациональные дроби и их интегрирование
Как мы увидим ниже, далеко не всякая элементарная функция имеет интеграл, выражающийся в элементарных функциях. Поэтому очень важно выделить такие классы функций , интегралы которых выражаются через элементарные функции. Простейшим из этих классов является класс рациональных функций.
Всякую рациональную функцию можно представить в виде рациональной дроби, т. е. в виде отношения двух многочленов:
![]()
Не ограничивая общности рассуждения, будем предполагать, что эти многочлены не имеют общих корней.
Если степень числителя ниже степени знаменателя, то дробь называется правильной, в противном случае дробь называется неправильной.
Если дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), можно представить данную дробь в виде суммы многочлена и некоторой правильной дроби:
![]() ;
;
здесь М(х)-многочлен, а ![]() - правильная дробь.
- правильная дробь.
Пример. Пусть дана неправильная рациональная дробь
![]()
Разделив числитель на знаменатель (по правилу деления многочленов), получим
![]() .
.
Так как интегрирование многочленов не представляет затруднений, то основная трудность при интегрировании рациональных дробей заключается в интегрировании правильных рациональных дробей.
Определение. Правильные рациональные дроби вида
(1). ![]()
(2). ![]() (k-целое положительное число
(k-целое положительное число![]()
(3) ![]() (корни знаменателя комплексные, т.е.
(корни знаменателя комплексные, т.е. ![]() ).
).
(4) ![]() (k-целое положительное число
(k-целое положительное число ![]() ;корни знаменателя комплексные), называются простейшими дробями (1),(2),(3) и (4) типов.
;корни знаменателя комплексные), называются простейшими дробями (1),(2),(3) и (4) типов.
Интегрирование простейших дробей типа (1),(2) и (3) не составляет большой трудности, поэтому мы приведем их интегрирование без каких-либо дополнительных пояснений:
(1) 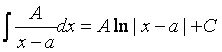
(2) 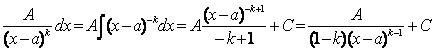
(3) 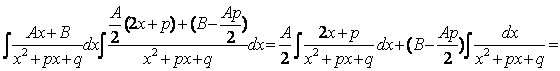
=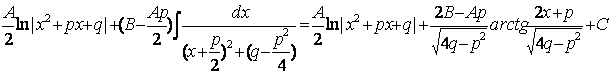
Более сложных вычислений требует интегрирование простейших дробей (4) типа. Пусть нам дан интеграл такого типа:
(4) 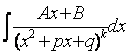
Произведем преобразования:
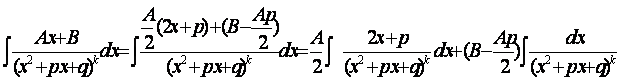
Первый интеграл берется подстановкой ![]() :
:
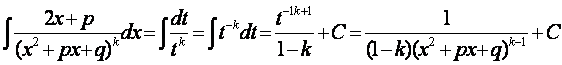
Второй интеграл- обозначим его через Ik-запишем в виде
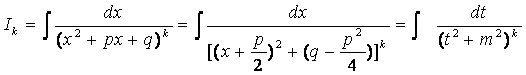 ,
,
полагая
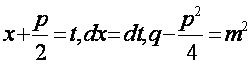
(по предположению корни знаменателя комплексные, а следовательно, ![]() ). Далее поступаем следующим образом:
). Далее поступаем следующим образом:
 .
.
Преобразуем интеграл:
![]()
Интегрируя по частям ,будем иметь
![]() .
.
Подставляя это выражение в равенство (1), получим
![]()
=![]()
=![]() .
.
В правой части содержится интеграл того же типа, что ![]() , но показатель степени знаменателя подынтегральной функции на единицу ниже
, но показатель степени знаменателя подынтегральной функции на единицу ниже ![]() ;таким образом, мы выразили
;таким образом, мы выразили ![]() через
через ![]() Продолжая идти тем же путем, дойдем до известного интеграла:
Продолжая идти тем же путем, дойдем до известного интеграла:
![]()
Подставляя затем всюду вместо t и m их значения, получим выражение интеграла (4) через х и заданные числа А, B, p,q.
Интегрирование рациональных дробей
Пусть требуется вычислить интеграл от рациональной дроби ![]() Если данная дробь неправильная, то мы представляем ее в виде суммы многочлена M(x) и правильной рациональной дроби
Если данная дробь неправильная, то мы представляем ее в виде суммы многочлена M(x) и правильной рациональной дроби ![]() . Последнюю же представляем по формуле в виде суммы простейших дробей. Таким образом, интегрирование всякой рациональной дроби сводится к интегрированию многочлена и нескольких простейших дробей.
. Последнюю же представляем по формуле в виде суммы простейших дробей. Таким образом, интегрирование всякой рациональной дроби сводится к интегрированию многочлена и нескольких простейших дробей.
Вид простейших дробей определяется корнями знаменателя f(x). Здесь возможны следующие случаи.
1.Случай.
Корни знаменателя действительны и различны, т. е.
F(x)=(x-a)(x-b)…(x-d).
В этом случае дробь ![]() разлагается на простейшие дроби 1типа:
разлагается на простейшие дроби 1типа:
![]()
и тогда
![]()
Похожие работы
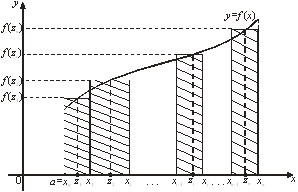
... дробей m и n; 2) если Z, то используется подстановка: a+bxn=ts, где s – знаменатель дроби 3) если Z, то применяется подстановка: ax-n+b=ts, где s – знаменатель дроби 9. Понятие определенного интеграла, его геометрический смысл. Определение. Если существует конечный передел интегральной суммы (8) - (8) при λ→0, не зависящий от способа разбиения &# ...
... предел функции Решение: Имеем неопределенность вида . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель , который при не равен нулю. В результате неопределенность будет раскрыта. 2. Производная и дифференциал Пусть функция определена в некоторой окрестности точки . Производной функции в точке называется предел отношения , когда ( ...
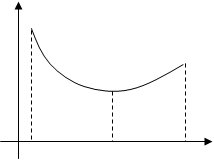
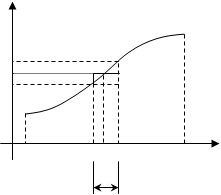
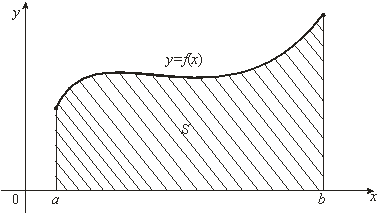
... выражением, – переменной интегрирования; отрезок называется промежутком интегрирования. Теорема 1. Если функция непрерывна на отрезке , то она интегрируема на этом отрезке. 2. Геометрический смысл определенного интеграла Пусть на отрезке задана непрерывная неотрицательная функция . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью ...
... переменных Z и z при произвольном изменении области G и переменных на кривой С. Очевидно, что при сделанных предположениях : Интеграл существует и является функцией комплексной переменной. Справедлива формула : (2) Эта формула устанавливает возможность вычисления производной от исходного интеграла путем дифференцирования подинтегральной функции по параметру. ТЕОРЕМА. Пусть f(Z) ...
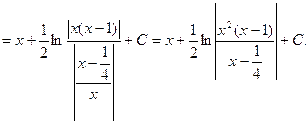

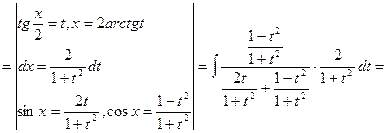


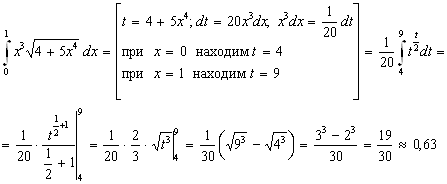
0 комментариев