Навигация
Дано: АВ=ВС=6, АК=КС=10, h=7, угол к плоскости 60, ОАВСК - пирамида, АВСК - четырехугольник
2.6. Дано: АВ=ВС=6, АК=КС=10, h=7, угол к плоскости 60, ОАВСК - пирамида, АВСК - четырехугольник.
Найти: VАВСКО.
Решение:
Двугранные углы при основании равны или 60° или 120°(по условию, но не обязательно 60°, в чем и состоит ловушка), вершина О проектируется в точку, равноудаленную от прямых, образующих четырехугольник, Þ АВСК - не параллелограмм, значит, две соседние стороны равны 6, а две другие, также соседние, 10.
Если у четырехугольника АВСК АВ=ВС=10, АК=КС=6, то существуют две равно - удаленные от его сторон точки (О1 и О2). Расстояния от проекции вершины О до сторон пирамиды равны 7/Ö3 (следствие из условия). Если проекция вершины - точка О1 (центр вписанной в АВСК окружности), то S АВСК=16×7/Ö3, но это невозможно, т.к. S АВСК £60
(наибольшая площадь достигается, если углы ÐКАВ и ÐВСК прямые, тогда
S АВСК = 1/2d1× d2×sin(d1d2)=1/2×8×15× sin 90°=60,Þвершина О проектируется в точку О2,расстояния от которой до сторон равны 7/Ö3, тогда SАВСК = =(10 - 6) 7/Ö3= 28/Ö3 , а VАВСКО=64/Ö3.
Ответ: VАВСКО=64/Ö3.
3. Частный случай.
Иногда поставленная задача оказывается настолько трудной, что не поддается решению, тогда используется следующий способ: решается часть задачи или рассматривается несколько задач, аналогичных данной, что и называется использованием “частного случая”. Бывает, что преподавателю не хватает какой-то простой задачи для иллюстрации новой теоремы, тогда тоже может помочь “частный случай”.
В истории есть примеры того, что обобщенные теоремы не находят применения, а их “частные случаи” получают широкое распространение и являются одними из важнейших среди прочих теорем математики (примером подобной ситуации может послужить теорема Паппа и ее “частный случай” теорема Пифагора).
Алгоритм конструирования:
Решение сложной конструкции
Детализирование задачи.
Изменение условий.
Объяснение возможного изменения решения.
Соединение и уточнение условий.
Решение полученной задачи.
Пример 6:Задача: "Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон. (Теорема Птолемея)" (ж. " Квант"№4 1991г.")3.1. Дано: окр., АВСК - вписанный четырехугольник, АС и ВК - диагонали.
Доказать: ВК × АС= СК ×АВ + ВС ×АК.
Доказательство:
Возьмем на диагонали АС точку М такую, что ÐАВМ= ÐСВК. Поскольку
![]()
![]()
![]()
![]()
![]() угол ÐСКВ=ÐМАВ (как вписанные), ВСК подобен АВМ, поэтому ВК: АВ=СК: АМ Û АВ×СК=АМ×ВК(1). Из того, что ÐАВК=ÐМВС (по построению), а Ð ВСМ= ÐАКВ (вписанные), следует, что АВК подобен МВС,ÞАК: СМ= ВК: ВСÛ АК×ВС=ВК× СМ (2).
угол ÐСКВ=ÐМАВ (как вписанные), ВСК подобен АВМ, поэтому ВК: АВ=СК: АМ Û АВ×СК=АМ×ВК(1). Из того, что ÐАВК=ÐМВС (по построению), а Ð ВСМ= ÐАКВ (вписанные), следует, что АВК подобен МВС,ÞАК: СМ= ВК: ВСÛ АК×ВС=ВК× СМ (2).
Сложив почленно (1) и (2), получаем ВК ×АС=СК ×АВ + ВС ×АК, что и требовалось доказать.
3.2. Итак, теорему можно поделить на группу терминов: "произведение диагоналей", "вписанный четырехугольник" и "сумма произведений противоположных сторон".
3.3. Для того чтобы получить частный случай теоремы Птолемея, выбран термин "вписанный четырехугольник", который изменяется на "вписанный квадрат".
3.4. В результате изменения условий, изменяется и решение: точка М переносится в центр окружности, который является и точкой пересечения диагоналей квадрата.
3.5. Полученная задача выглядит так: “Докажите, что квадрат стороны вписанного квадрата равен двум площадям этого квадрата”. (Составлена самостоятельно).
3.6. Решение:
Дано: АВСК - вписанный квадрат, АС и ВК - диагонали, О - центр окружности.
Доказать: ВК× ВК=2 SАВСК.
![]()
![]()
![]() Доказательство:
Доказательство:
Т.к. ÐАВО=ÐСВК (диагональ квадрата является биссектрисой),
![]()
![]() ÐСКВ=ÐОАВ (вписанные), ВСК подобен АВК,Þ АВ×АВ= АО×ВК (1).
ÐСКВ=ÐОАВ (вписанные), ВСК подобен АВК,Þ АВ×АВ= АО×ВК (1).
![]()
![]() Т.к.ÐАВК=ÐОВС (аналогично ÐАВО=ÐСВК), ÐВСО=ÐАОВ (вписанные), АВК подобен ОВС, Þ ВА×ВА=ВК×СО (2).
Т.к.ÐАВК=ÐОВС (аналогично ÐАВО=ÐСВК), ÐВСО=ÐАОВ (вписанные), АВК подобен ОВС, Þ ВА×ВА=ВК×СО (2).
Сложив(1)и(2),получаем: ВК×ВК=ВА×ВА, т.к. ВА×ВА=2SАВСК, ВК×ВК=2SАВСК, что и требовалось доказать.
Хочется отметить, что "Частный случай" всегда решается проще образовавшей его задачи.
В некоторых случаях между данными и искомыми величинами в задаче общего характера существует сложная зависимость, и решить эту задачу элементарными методами не удается, в то время как частная задача этого типа имеет вполне простое и красивое решение.
4. Варьирование условий.
Варьирование условий - способ конструирования задач, который может изменить решение и результат задачи путем замены всего одного слова, например, задача на построение треугольника по трем сторонам имеет элементарное решение, а если заменить "стороны" на "биссектрисы", решение многократно усложняется. Варьирование условий зачастую приводит к образованию целых циклов задач, очень похожих друг на друга по звучанию, но совершенно различных по типу и сложности решения. Варьирование бывает разным: в первом случае изменяется определение или термин, во втором - равенство или неравенство, причем эти два способа довольно сильно отличаются на практике, хотя и схожи в теории.
Алгоритм конструирования:
4.1. Выделение условий для изменения.
4.2. Изменение выбранных условий.
4.3. Уточнение формулировки.
Пример 7:
Задача: "На плоскости даны две точки: А и В. Найдите геометрическое место точек плоскости С таких, что для треугольника АВС имеет место равенство: ahа=вhв (где hа и hв - высоты, опущенные на стороны а и в). (ж. "Квант" №9, 1991г.)
4.1. Т. к. в задаче используется равенство, то для изменения выбраны его члены: а и в .
4.2. Пусть а изменится на проведенную к ней медиану ма, а в - на медиану мв.
4.3. Итоговая формулировка: "На плоскости даны две точки: А и В, найдите геометрическое место точек С таких, что для треугольника имеет место равенство:
мв× hа=hв× ма", (ж. “ Квант”).
5. Обобщение.
Обобщение - один из первых способов получения новых задач и теорем, хотя далеко не каждую задачу или теорему можно обобщить. Бурный процесс обобщения математических знаний и создание все более и более абстрактных теорий начались в девятнадцатом веке, и продолжается до сих пор.
В процессе развития математики многие математические понятия претерпевали значительные изменения в сторону обобщения. Некоторые первоначальные определения с более общей точки зрения оказывались неудачными, и их приходилось изменять, давать новые наименования.
Алгоритм конструирования:
5.1. Выявление возможности обобщения.
5.2. Обобщение выбранного факта.
5.3. Уточнение формулировки.
Обобщение - очень емкое понятие, это и получение более абстрактных понятий, и перенос утверждения на более широкое множество объектов, и получение новых интерпретаций, и перенос утверждения задачи из плоскости в пространство. С одним из самых простых обобщений является преобразование числовой задачи, путем замены числовых данных буквами-символами. Как ни элементарно подобное обобщение, оно может привести к интересным выводам, а иногда и к созданию новых формул.
Пример 8:
Теорема: "Основание хотя бы одной высоты треугольника лежит на соответствующей стороне, а не на ее продолжении", (ж. "Квант" №9, 1991г.)
5.1. Возможно перенести утверждение теоремы из плоскости в пространство, а конкретнее: изменить плоскую фигуру на объемную.
5.2. Термин "Треугольник" при выходе в пространство трансформируется в "тетраэдр"
5.3. Новая теорема выглядит так: "Для любого тетраэдра основание хотя бы одной высоты принадлежит соответствующей грани тетраэдра". (ж. “Квант”).
Заключение.
Материал, представленный в данной работе, имеет значение как для учителей, так и для учащихся. Свое применение для педагогов он может найти как пособие для составления задач конкретно к каждому уроку, если в учебниках и различных методических пособиях не найдется необходимых сведений. Учащимся данная работа поможет не растеряться перед сложной или объемной задачей, потому что, зная как задача была составлена, найти решение гораздо проще.
Разобранная тема необходима для изучения истории возникновения задач, для составления и решения как простых, так и сложных не только математических, но и жизненных заданий. Возможно, ее значение для большой науки не так уж велико, но на примере разобранных в ней приемов конструирования можно научится выделять опорные пункты в задаче, или же наоборот, обобщать. Важно то, что данная тема – путь к бесконечному творчеству, а какой его вид выберет человек – решать только ему.
Список литературы
Н.П. Тучнин "Как задать вопрос?"
И. Шарыгин "Откуда берутся задачи?"
А.В. Погорелов "Геометрия 7-11"
Журналы "Квант"
М.И. Сканави "Сборник задач по математике для поступающих в ВУЗы"
В.М. Финкельштейн "Когда задача не выходит".
Похожие работы
... и искомыми величинами в задаче общего характера существует сложная зависимость, и решить эту задачу элементарными методами не удается, в то время как частная задача этого типа имеет вполне простое и красивое решение. 4. ВАРЬИРОВАНИЕ УСЛОВИЙ. Варьирование условий - способ конструирования задач, который может изменить решение и результат задачи путем замены всего одного слова, например, ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
... в разработке методов превращения разнообразной конструкторской документации в цифровую форму и представлении всех задач и элементов процесса проектирования только в виде операций над числами и логическими выражениями с доведением их до алгоритмов и машинных программ. Но при автоматизации проектно-конструкторского процесса следует постоянно помнить, что ЭВМ — это вспомогательное средство, а не ...
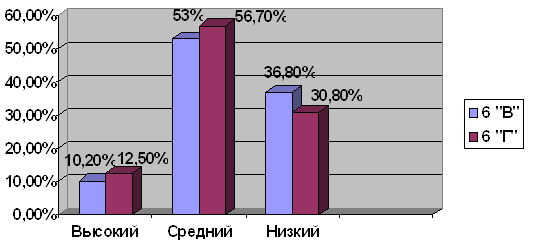
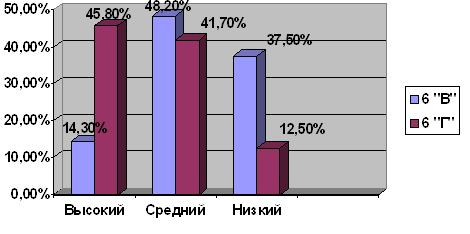
... и перенести полученные знания на практику. Глава 2. Работа учителя по развитию логического мышления на уроках математики 2.1 Опытно-экспериментальная работа и анализ ее результатов Опытно-экспериментальное исследование по выявлению уровня развития логического мышления школьников при решении текстовых задач проводилось на базе МОУ «Средняя общеобразовательная школа № 10» г. Кунгура в ...

0 комментариев