Навигация
1. ò xÖ(3x2–1)dx;
Пусть 3x2–1=t (t³0), возьмем производную от обеих частей:
6xdx = dt
xdx=dt/6
3
ó dt 1 1 ó 1 1 t 2 2 1 ———Ø
ô— t 2 = — ô t 2dt = – ——– + C = —Ö 3x2–1 +C
õ 6 6 õ 6 3 9
2. t
ò sin x cos 3x dx = ò – t3dt = – – + C
4
Пусть cos x = t
-sin x dx = dt
Метод преобразования подынтегральной функции в сумму или разность:
Примеры :
ò sin 3x cos x dx = 1/2 ò (sin 4x + sin 2x) dx = 1/8 cos 4x – ¼ cos 2x + C
ó x4+3x2+1 ó 1 1
ô———— dx = ô( x2+2 – ——– ) dx = — x2 + 2x – arctg x + C
õ x2+1 õ x2+1 3
Примечание: при решении этого примера хорошо делать многочлены ”углом”.
По частям
Если в заданном виде взять интеграл невозможно, а в то же время, очень легко находится первообразная одного множителя и производная другого, то можно использовать формулу.
(u(x)v(x))’=u’(x)v(x)+u(x)v(x)
u’(x)v(x)=(u(x)v(x)+u(x)v’(x)
Проинтегрируем обе части
ò u’(x)v(x)dx=ò (u(x)v(x))’dx – ò u(x)v’(x)dx
ò u’(x)v(x)dx=u(x)v(x)dx – ò u(x)v’(x)dx
Примеры:
ò x cos (x) dx = ò x dsin x = x sin x – ò sin x dx = x sin x + cos x + C
x = u(x)
cos x = v’(x)
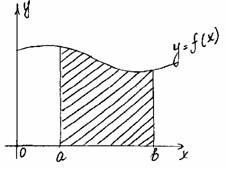
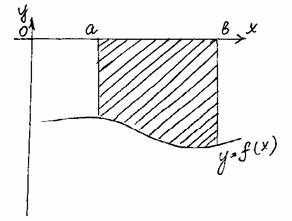
Криволинейная трапецияОпределение. Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абцисс и прямыми x=a, x=b, называется криволинейной трапецией.
Способы нахождения площади криволинейной трапеции
Теорема. Если f(x) непрерывная и неотрицательная функция на отрезке [a;b], то площадь соответствующей криволинейной трапеции равна приращению первообразных.
Дано: f(x)– непрерывная неопр. функция, xÎ[a;b].
Доказать: S = F(b) – F(a), где F(x) – первообразная f(x).
Доказательство:
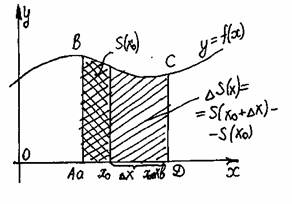
|
| 1) Рассмотрим вспомогательную функцию S(x). Каждому xÎ[a;b] поставим в соответствие ту часть криволинейной трапеции, которая лежит левее прямой, проходящей через точку с этой абциссой и параллельно оси ординат. Следовательно S(a)=0 и S(b)=Sтр |
Докажем, что S(a) – первообразная f(x).
D( f ) = D(S) = [a;b]
S’(x0)= lim( S(x0+Dx) – S(x0) / Dx ), при Dx®0 DS – прямоугольник
Dx®0 со сторонами Dx и f(x0)
S’(x0) = lim(Dx f(x0) /Dx) = lim f(x0)=f(x0): т.к. x0 точка, то S(x) –
Dx®0 Dx®0 первообразная f(x).
Следовательно по теореме об общем виде первообразной S(x)=F(x)+C.
Т.к. S(a)=0, то S(a) = F(a)+C
C = –Fa
S = S(b)=F(b)+C = F(b)–F(a)
II.
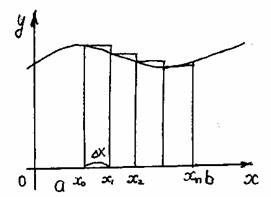
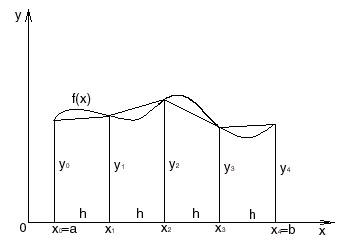
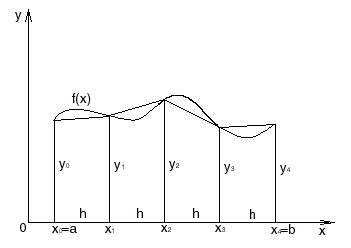
|
| 1). Разобьем отрезок [a;b] на n равных частей. Шаг разбиения Dx=(b–a)/n. При этом Sтр=lim(f(x0)Dx+f(x1)Dx+...+f(xn))Dx= n®¥ = lim Dx(f(x0)+f(x1)+...+f(xn)) При n®¥ получим, что Sтр= Dx(f(x0)+f(x1)+...+f(xn)) |
Предел этой суммы называют определенным интегралом.
b
Sтр=ò f(x)dx
a
Сумма стоящая под пределом, называется интегральной суммой.
Определенный интеграл это предел интегральной суммы на отрезке [a;b] при n®¥. Интегральная сумма получается как предел суммы произведений длины отрезка, полученного при разбиении области определения функции в какой либо точке этого интервала.
a — нижний предел интегрирования;
b — верхний.
Формула Ньютона–Лейбница.
Сравнивая формулы площади криволинейной трапеции делаем вывод:
если F – первообразная для b на [a;b], то
b
ò f(x)dx = F(b)–F(a)
a
b b
ò f(x)dx = F(x) ô = F(b) – F(a)
a a
Свойства определенного интеграла.
1.
b b
ò f(x)dx = ò f(z)dz
a a
2.
a
ò f(x)dx = 0
a
a
ò f(x)dx = F(a) – F(a) = 0
a
3.
b a
ò f(x)dx = – ò f(x)dx
a b
b a
ò f(x)dx = F(a) – F(b) ò f(x)dx = F(b) – F(a) = – (F(a) – F(b))
a b
Если a, b и c любые точки промежутка I, на котором непрерывная функция f(x) имеет первообразную, то
b c b
ò f(x)dx = ò f(x)dx + ò f(x)dx
a a c
F(b) – F(a) = F(c) – F(a) + F(b) – F(c) = F(b) – F(a)
(это свойство аддитивности определенного интеграла)
Если l и m постоянные величины, то
b b b
ò (lf(x) +m j(x))dx = l ò f(x)dx + m òj(x))dx –
a a c
– это свойство линейности определенного интеграла.
6.
b b b b
ò (f(x)+g(x)+...+h(x))dx = ò f(x)dx+ ò g(x)dx+...+ ò h(x)dx
a a a a
b
ò (f(x)+g(x)+...+h(x))dx = (F(b) + G(b) +...+ H(b)) –
a
– (F(a) + G(a) +...+ H(a)) +C =
= F(b)–F(a)+C1 +G(b)–G(a)+C2+...+H(b)–H(a)+Cn=
b b b
= ò f(x)dx+ ò g(x)dx+...+ ò h(x)dx
a a a
Набор стандартных картинок
|
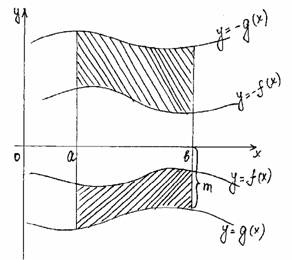
| Т.к. f(x)<0, то формулу Ньютона-Лейбница составить нельзя, теорема верна только для f(x)³0. Надо: рассмотреть симметрию функции относительно оси OX. ABCD®A’B’CD b S(ABCD)=S(A’B’CD) = ò –f(x)dx a |
|
| b b S= ò f(x)dx = ò g(x)dx a a |
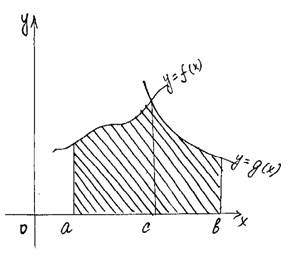
|
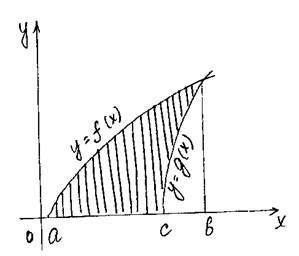
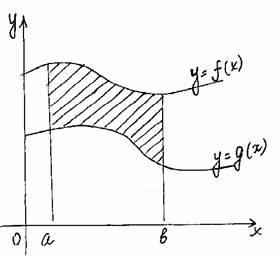
| c b S = ò (f(x)–g(x))dx+ò(g(x)–f(x))dx a c |
|
| f(x)® f(x)+m g(x)®g(x)+m b S= ò (f(x)+m–g(x)–m)dx = a b = ò (f(x)– g(x))dx a Если на отрезке [a;b] f(x)³g(x), то площадь между этими графиками равна b ò ((f(x)–g(x))dx a |
|
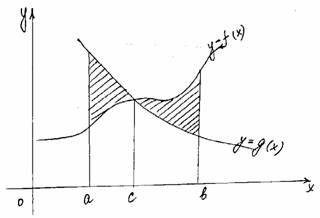
| Функции f(x) и g(x) произвольные и неотрицательные b b b S=ò f(x)dx – ò g(x)dx = ò (f(x)–g(x))dx a a a |
|
| b b S=ò f(x)dx + ò g(x)dx a a |
I. В физике.
Работа силы (A=FScosa, cosa ¹ 1)
Если на частицу действует сила F, кинетическая энергия не остается постоянной. В этом случае согласно
d(mu2/2) = Fds
приращение кинетической энергии частицы за время dt равно скалярному произведению Fds, где ds – перемещение частицы за время dt. Величина
dA=Fds
называется работой, совершаемой силой F.
Пусть точка движется по оси ОХ под действием силы, проекция которой на ось ОХ есть функция f(x) (f–непрерывная функция). Под действием силы точка переместилась из точки S1(a) в S2(b). Разобьем отрезок [a;b] на n отрезков, одинаковой длины Dx = (b – a)/n. Работа силы будет равна сумме работ силы на полученных отрезках. Т.к. f(x) –непрерывна, то при малом [a;x1] работа силы на этом отрезке равна f(a)(x1–a). Аналогично на втором отрезке f(x1)(x2–x1), на n-ом отрезке — f(xn–1)(b–xn–1). Следовательно работа на [a;b] равна:
А » An = f(a)Dx +f(x1)Dx+...+f(xn–1)Dx=
= ((b–a)/n)(f(a)+f(x1)+...+f(xn–1))
Приблизительное равенство переходит в точное при n®¥
b
А = lim [(b–a)/n] ( f(a)+...+f(xn–1))= ò f(x)dx (по определению)
n®¥ a
Пример.
Пусть пружина жесткости С и длины l сжата на половину свой длины. Определить величину потенциальной энергии Ер равна работе A, совершаемой силой –F(s) упругость пружины при её сжатии, то
l/2
Eп = A= – ò (–F(s)) dx
0
Из курса механики известно, что F(s)= –Cs.
Отсюда находим
l/2 l/2
Еп= – ò (–Cs)ds = CS2/2 | = C/2 l2/4
0 0
Ответ: Cl2/8.
Координаты центра масс
Центр масс – точка через которую проходит равнодействующая сил тяжести при любом пространственном расположении тела.
Пусть материальная однородная пластина о имеет форму криволинейной трапеции {x;y |a£x£b; 0£y£f(x)} и функция y=f(x) непрерывна на [a;b], а площадь этойкриволинейной трапеции равна S, тогда координаты центра масс пластины о находят по формулам:
b b
x0 = (1/S) ò x f(x) dx; y0 = (1/2S) ò f 2(x) dx;
a a
Примеры.
Центр масс.
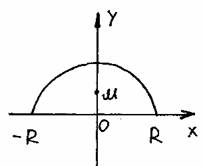
Найти центр масс однородного полукруга радиуса R.
Изобразим полукруг в системе координат OXY.
|
| Из соображений симметрии и однородности замечаем, что абсцисса точки M xm=0 Функция, описывающая полукруг имеет вид: y = Ö(R2–x2) Пусть S = pR2/2 — площадь полукруга, тогда |
R R
y = (1/2S) òÖ(R2–x2)dx = (1/pR2) òÖ(R2–x2)dx =
–R –R
R
= (1/pR2)(R2x–x3/3)|= 4R/3p
–R
Ответ: M(0; 4R/3p )
Путь, пройденный материальной точкой
Если материальная точка движется прямолинейно со скоростью u=u(t) и за время T= t2–t1 (t2>t1) прошла путь S, то
t2
S=ò u(t)dt.
t1
В геометрии
Объём — количественная характеристика пространственного тела. За единицу измерения объёма принимают куб с ребром 1мм(1ди, 1м и т.д.).
Количество кубов единичного объёма размещенных в данном теле — объём тела.
Аксиомы объёма:
Объём — это неотрицательная величина.
Объём тела равен сумме объёмов тел, его составляющих.
Найдем формулу для вычисления объёма:
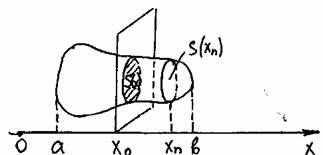
выберем ось ОХ по направлению расположения этого тела;
определим границы расположения тела относительно ОХ;
введем вспомогательную функцию S(x) задающую следующее соответствие: каждому x из отрезка [a;b] поставим в соответствие площадь сечения данной фигуры плоскостью, проходящей через заданную точку x перпендикулярно оси ОХ.
разобьем отрезок [a;b] на n равных частей и через каждую точку разбиения проведём плоскость перпендикулярную оси ОХ, при этом наше тело разобьется на части. По аксиоме
V=V1+V2+...+Vn=lim(S(x1)Dx +S(x2)Dx+...+S(xn)Dx
n®¥
Dx®0, а Sk®Sk+1, а объем части, заключенной между двумя соседними плоскостями равна объему цилиндра Vц=SоснH.
Имеем сумму произведений значений функций в точках разбиения на шаг разбиения, т.е. интегральную сумму. По определению определенного интеграла, предел этой суммы при n®¥ называется интегралом a
ò S(x)dx
b
a
V= ò S(x)dx, где S(x) – сечение плоскости, проходящей через
b выбранную точку перпендикулярно оси ОХ.
Для нахождения объема надо:
1). Выбрать удобным способом ось ОХ.
2). Определить границы расположения этого тела относительно оси.
3). Построить сечение данного тела плоскостью перпендикулярно оси ОХ и проходящей через соответственную точку.
4). Выразить через известные величины функцию, выражающую площадь данного сечения.
5). Составить интеграл.
6). Вычислив интеграл, найти объем.
Объем фигур вращения
Тело, полученное в результате вращения плоской фигуры, относительно какой-то оси, называют фигурой вращения.
Функция S(x) у фигуры вращения есть круг.
Sсеч = pr2
Sсеч(x)=p f 2(x)
b
V= ò f 2(x)
a
Длина дуги плоской кривой
Пусть на отрезке [a;b] функция y = f(x) имеет непрерывную производную y’ = f ’(x). В этом случае длину дуги l “куска” графика функции y = f(x), xÎ[a;b] можно найти по формуле
b
l = ò Ö(1+f’(x)2)dx
a
Список литературыМ.Я.Виленкин, О.С.Ивашев–Мусатов, С.И.Шварцбурд, “Алгебра и математический анализ”, Москва,1993г.
“Сборник задач по математическому анализу”, Москва,1996г.
И.В.Савельев, “Курс общей физики”, том 1, Москва, 19
Похожие работы
... они не требуют от учащихся дополнительных знаний по физике, а, следовательно, удовлетворяют как принципу научности, так и принципу доступности материала. 2.2. Изучение свойств определенного интеграла с помощью физических моделей При изучении интеграла существенным является отбор свойств, которые необходимо знать ученикам. Их должно быть достаточно для рассмотрения приложений интеграла и в ...
... , разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*. §2. Оценка погрешности метода Монте-Карло. Пусть для получения оценки a* математического ожидания а случайной величины Х было произведено n независимых испытаний (разыграно n возможных значений Х) и по ...
... с помощью метода трапеций. Программа состоит из трех функций main, f и trap. Функция main позволяет ввести интервалы интегрирования и задать точность вычисления интеграла, а также вызывает функцию trap для вычисления интеграла и распечатывает на экране результат. Функция f принимает аргумент x типа float и возвращает значение интегрируемой функции в этой точке. Trap – основная функция программы: ...
... этом отрезке функция непрерывна. Для выполнения поставленной задачи составлена нижеописанная программа, приближенно вычисляющая определенный интеграл с помощью метода трапеций. Программа состоит из трех функций main, f и trap. Функция main позволяет ввести интервалы интегрирования и задать точность вычисления интеграла, а также вызывает функцию trap для вычисления интеграла и распечатывает на ...
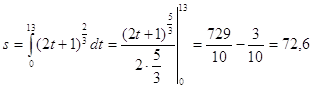



0 комментариев