Навигация
Симметрии многогранника системы независимости
Пусть E = { e1,e2,,en} - некоторое множество мощности n. Системой независимости на множестве E называется непустое семейство J его подмножеств, удовлетворяющее условию: если J![]()
![]() и I
и I![]() , то I
, то I![]() .
.
Множества семейства ![]() называется независимыми множествами. Максимальные по включению множества из
называется независимыми множествами. Максимальные по включению множества из ![]() называются базисами.
называются базисами.
Автоморфизмом системы независимости ![]() называется такое взаимооднозначное отображение множества E на себя, что (I){(e) | eI}
называется такое взаимооднозначное отображение множества E на себя, что (I){(e) | eI}![]() для любого независимого множества I. Группу автоморфизмов системы независимости
для любого независимого множества I. Группу автоморфизмов системы независимости ![]() будем обозначать через Aut(
будем обозначать через Aut(![]() ).
).
Пусть RE - евклидово пространство, ассоциированное с E посредством взаимоодназначного соответствия между множеством координатных осей пространства RE и множеством E. Иными словами, RE можно понимать как совокупность вектор-столбцов размерности n с вещественными компонентами, индексированными элементами множества E. Всякому S E сопоставим его вектор инциденций по правилу: xSe= 1 при eS , xSe= 0 при eS. Очевидно, что это правило задает взаимооднозначное соответствие между 2E и вершинами единичного куба в RE. Многогранник системы независимости ![]() определим как P(
определим как P(![]() ) = Conv(xI | I
) = Conv(xI | I![]() ). Ясно, что векторы инциденций независимых множеств системы независимости
). Ясно, что векторы инциденций независимых множеств системы независимости ![]() , и только они, являются вершинами многогранника P(
, и только они, являются вершинами многогранника P(![]() ) [4].
) [4].
Пусть PRE - произвольный многогранник. Симметрией многогранника P назовем такое невырожденное аффинное преобразование пространства RE, что (P){(x) | xP}=P. Как известно, всякое невырожденное аффинное преобразование определяется невырожденной (nn)-матрицей A и сдвигом hRE, то есть (x)=Ax+h при xRE [1]. Очевидно, что невырожденное аффинное преобразование пространства RE является симметрией многогранника P(![]() ) тогда и только тогда, когда для любого I
) тогда и только тогда, когда для любого I![]() существует такое J
существует такое J![]() , что (xI) = xJ.
, что (xI) = xJ.
Симметрию с нулевым сдвигом будем называть линейной симметрией. Очевидно, что множество всех симметрий многогранника P является группой относительно суперпозиции отображений, а множество линейных симметрий - ее подгруппой. Группу симметрий многогранника P мы будем обозначать через S(![]() ), а ее подгруппу линейных симметрий - через L(
), а ее подгруппу линейных симметрий - через L(![]() ).
).
Ранее в [3] была доказана изоморфность групп L(![]() ) и Aut(
) и Aut(![]() ) для матроида
) для матроида ![]() , в [2] - изоморфность группы линейных симметрий многогранника паросочетаний и группы автоморфизмов соответствующего графа. Пользуясь аналогичными методами, легко доказать изоморфность групп L(
, в [2] - изоморфность группы линейных симметрий многогранника паросочетаний и группы автоморфизмов соответствующего графа. Пользуясь аналогичными методами, легко доказать изоморфность групп L(![]() ) и Aut(
) и Aut(![]() ) для произвольной системы независимости
) для произвольной системы независимости ![]() .
.
В настоящей работе показано, что группа симметрий многогранника системы независимости выписывается с помощью подгруппы L(![]() ) и семейства некоторых специальных преобразований пространства RE.
) и семейства некоторых специальных преобразований пространства RE.
Рассмотрим задачу комбинаторной оптимизации на системе независимости с аддитивной целевой функцией:
|
| (1) |
где ve0 - вес элемента eE. Пусть имеется симметрия многогранника P со сдвигом xH. Тогда задача (1) сводится к задаче, размерность которой не больше, чем E-H.
Ниже приведены понятия и факты, необходимые для дальнейшего изложения.
Пусть H![]() . H-отображением будем называть линейное невырожденное преобразование пространства RE, удовлетворяющее условию: для любого I
. H-отображением будем называть линейное невырожденное преобразование пространства RE, удовлетворяющее условию: для любого I![]() существует такое J
существует такое J![]() , что (xI) = xJH, где под JH подразумевается симметрическая разность множеств J и H.
, что (xI) = xJH, где под JH подразумевается симметрическая разность множеств J и H.
Без ограничения общности будем считать, что размерность многогранника P равна n, ибо в противном случае существует элемент eЕ, не содержащийся ни в каком независимом множестве и, следовательно, вместо E можно рассматривать множество E{e} .
Похожие работы
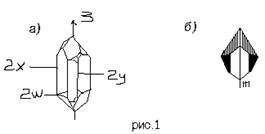
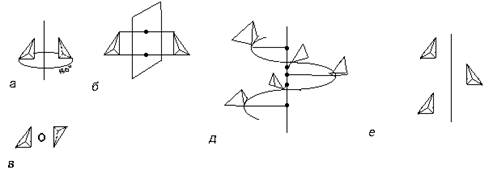
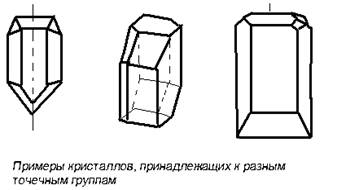
... , а затем и более фундаментального, одновременно и самого абстрактного (динамического) понимания симметрии. 2. 2.2.Симметрия кристаллов. Правильную, симметричную форму кристаллов издавна объясняли симметричным расположением атомов. Само существование атомов было еще гипотезой, но внешнее проявление стройного порядка заставляло предполагать внутреннюю причину. Быть может, правильные пирамиды, ...
... имеют достаточно четкое и правильное представление из собственного жизненного опыта, а формулировки которых являются слишком громоздкими. Выводы по § 1 1. Основные цели изучения темы «Объемы многогранников» в курсе стереометрии – развитие пространственных представлений учащихся, освоение способов вычисления практически важных величин и дальнейшее развитие логического мышления учащихся. ...
... . Реакции узлов более высокого уровня менее зависят от позиции и более устойчивы к искажениям. Структура Неокогнитрон имеет иерархическую структуру, ориентированную на моделирование зрительной системы человека. Он состоит из последовательности обрабатывающих слоев, организованных в иерархическую структуру (рис. 10.8). Входной образ подается на первый слой и передается через плоскости, ...
... , только если, например, нагреть кристалл так, чтобы он начал плавится. Порядок, закономерность, периодичность, симметрия расположения атомов - вот что характерно для кристаллов. Во всех кристаллах, во все твердых веществах частицы расположены правильным, четким строем, выстроены симметричным, правильным повторяющимся узором. Пока есть этот порядок существует твердое тело, кристалл. Нарушен ...
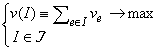
0 комментариев