Навигация
2.2.2. Тестовый пример.
4,1x1 + 0,1x2 + 0,2x3 + 0,2x4 = 21,14 ,
0,3x1 + 5,3x2 + 0,9x3 – 0,1x4 = – 17,82 ,
0,2x1 + 0,3x2 + 3,2x3 + 0,2x4 = 9,02 ,
0,1x1 + 0,1x2 + 0,2x3 – 9,1x4 = 17,08 ,
x1 = 5,2, x2 = –4,2, x3 = 3, x4 = –1,8.
2.2.3. Описание алгоритма. В переменную n вводится порядок матрицы системы, в переменную e – максимальная абсолютная погрешность. С помощью вспомогательной процедуры ReadSystem в двумерный массив a и одномерный массив b вводится c клавиатуры расширенная матрица системы. Начальное прибижение предполагается равным нулю. Оба массива и переменные n и e передаются функции Seidel. В функции Seidel исследуется сходимость системы, и в том случае если система не сходится, выполнение функции прекращается с результатом false. В ходе каждой итерации вычисляется новое приближение и и абсолютная погрешность. Когда полученная погрешность становится меньше заданной, выполнение функции прекращается. Полученное решение выводится на экран при помощи вспомогательной процедуры WriteX.
2.2.4. Листинг программы и результаты работы.
Uses CRT;
Const
maxn = 10;
Type
Data = Real;
Matrix = Array[1..maxn, 1..maxn] of Data;
Vector = Array[1..maxn] of Data;
{ Процедура ввода расширенной матрицы системы }
Procedure ReadSystem(n: Integer; var a: Matrix; var b: Vector);
Var
i, j, r: Integer;
Begin
r := WhereY;
GotoXY(2, r);
Write('A');
For i := 1 to n do begin
GotoXY(i * 6 + 2, r);
Write(i);
GotoXY(1, r + i + 1);
Write(i:2);
end;
GotoXY((n + 1) * 6 + 2, r);
Write('b');
For i := 1 to n do begin
For j := 1 to n do begin
GotoXY(j * 6 + 2, r + i + 1);
Read(a[i, j]);
end;
GotoXY((n + 1) * 6 + 2, r + i + 1);
Read(b[i]);
end;
End;
{ Процедура вывода результатов }
Procedure WriteX(n :Integer; x: Vector);
Var
i: Integer;
Begin
For i := 1 to n do
Writeln('x', i, ' = ', x[i]);
End;
{ Функция, реализующая метод Зейделя }
Function Seidel(n: Integer; a: Matrix; b: Vector; var x: Vector; e: Data) :Boolean;
Var
i, j: Integer;
s1, s2, s, v, m: Data;
Begin
{ Исследуем сходимость }
For i := 1 to n do begin
s := 0;
For j := 1 to n do
If j i then
s := s + Abs(a[i, j]);
If s >= Abs(a[i, i]) then begin
Seidel := false;
Exit;
end;
end;
Repeat
m := 0;
For i := 1 to n do begin
{ Вычисляем суммы }
s1 := 0;
s2 := 0;
For j := 1 to i - 1 do
s1 := s1 + a[i, j] * x[j];
For j := i to n do
s2 := s2 + a[i, j] * x[j];
{ Вычисляем новое приближение и погрешность }
v := x[i];
x[i] := x[i] - (1 / a[i, i]) * (s1 + s2 - b[i]);
If Abs(v - x[i]) > m then
m := Abs(v - x[i]);
end;
Until m < e;
Seidel := true;
End;
Var
n, i: Integer;
a: Matrix;
b, x: Vector;
e: Data;
Begin
ClrScr;
Writeln('Программа решения систем линейных уравнений по методу Зейделя');
Writeln;
Writeln('Введите порядок матрицы системы (макс. 10)');
Repeat
Write('>');
Read(n);
Until (n > 0) and (n 0) and (e < 1);
Writeln;
Writeln('Введите расширенную матрицу системы');
ReadSystem(n, a, b);
Writeln;
{ Предполагаем начальное приближение равным нулю }
For i := 1 to n do
x[i] := 0;
If Seidel(n, a, b, x, e) then begin
Writeln('Результат вычислений по методу Зейделя');
WriteX(n, x);
end
else
Writeln('Метод Зейделя не сходится для данной системы');
Writeln;
End.
Программа решения систем линейных уравнений по методу Зейделя
Введите порядок матрицы системы (макс. 10)
>4
Введите точность вычислений
>.000001
Введите расширенную матрицу системы
A 1 2 3 4 b
1 4.1 0.1 0.2 0.2 21.14
2 0.3 5.3 0.9 -0.1 -17.82
3 0.2 0.3 3.2 0.2 9.02
4 0.1 0.1 0.2 -9.1 17.08
Результат вычислений по методу Зейделя
x1 = 5.2000000008E+00
x2 = -4.2000000028E+00
x3 = 3.0000000003E+00
x4 = -1.80000000
Похожие работы
... 10.4 9.7 9.7 -8.4 Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = b1 , a21x2 + ...
... матрицы могут вычисляться по следующим формулам: 6. Метод квадратного корня Использование разложения на взаимно транспонированные треугольные матрицы при решении систем алгебраических уравнений называется метод квадратного корня. Метод разложения на транспонированные треугольные матрицы имеет модификацию, заключающуюся в выделении в произведении диагональной матрицы D с элементами на ...
... вычисляют в следующем порядке: xjn, xjn–1, …, xj1. 3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений Ax = b с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду x = Bx + c. Здесь B – квадратная матрица с элементами bij (i, ...
... на языке Turbo Pascal 7.0 для решении систем линейных алгебраических уравнений, используя метод простой итерации. 1.2 Математическая формулировка задачи Пусть А – невырожденная матрица и нужно решить систему где диагональные элементы матрицы А ненулевые. 1.3 Обзор существующих численных методов решения задачи Метод Гаусса В методе Гаусса матрица СЛАУ с помощью равносильных ...



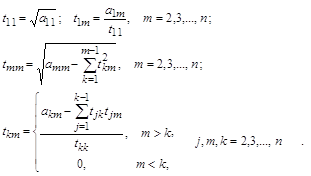
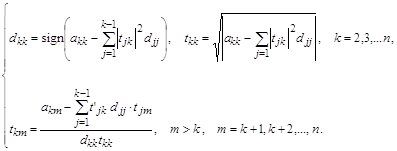
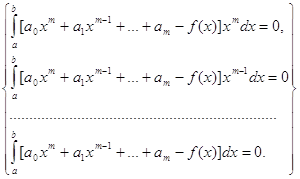
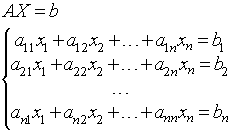
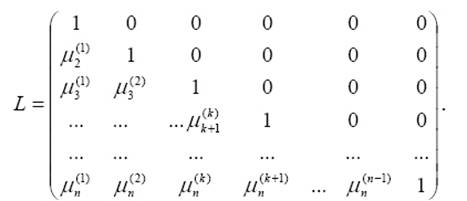
0 комментариев