Навигация
Разложение ф-ций в степенные ряды. Ряды Тейлора и Маклорена
2 Разложение ф-ций в степенные ряды. Ряды Тейлора и Маклорена.
Пусть![]() (1) сходится при |x-x0|<R а его сумма является ф-лой f(x)=
(1) сходится при |x-x0|<R а его сумма является ф-лой f(x)= ![]() (2) В этом случае говорят, что ф-ция f(x) разложена в степенной ряд. (1) .
(2) В этом случае говорят, что ф-ция f(x) разложена в степенной ряд. (1) .
Т1 Если ф-ция f распространяется в некоторой окрестности т. х0 f(x)= ![]() , то
, то ![]()
и справедлива формула: ![]()
![]() (15) Если в некоторой окрестности заданной точки ф-ция распадается в степенной ряд, то это разложение единственно.
(15) Если в некоторой окрестности заданной точки ф-ция распадается в степенной ряд, то это разложение единственно.
Пусть дествит. ф-ция f определена в некоторой окрестности т. х0 и имеет в этой точке производные всех порядков, тогда ряд:![]() (6) наз рядом Тейлора ф-ции f в т, х0
(6) наз рядом Тейлора ф-ции f в т, х0
При х0=0 ряд Тейлора принимает вид:
![]() (6’) и называется ряд Маклорена.
(6’) и называется ряд Маклорена.
Ряд Тейлора может:
1 Расходится всюду, кроме х=х0
2 Сходится, но не к исходной ф-ции f(x), а к какой-нибудь другой.
3 Сходится к исходной ф-ции f(x)
Бесконечная дифференцируемость ф-ции f(x) в какой-то т. х0 является необходимым условием разложимости ф-ции в ряд Тейлора, но не является достаточным. Для введения дополнительных условий треб. ф-ла Тейлора.
Т2 Если ф-ция f(x) (n+1) раз дифференцируема на интервале (x0-h, x0+h) h>0, то для всех x Î (x0-h, x0+h) имеет место ф-ла Тейлора:
 где остаток rn(x) можно записать:
где остаток rn(x) можно записать:
![]() (8)
(8)
![]() (9) Формула (8) наз остаточным членом ф-лы Тейлора в интегральной форме. Ф-ла (9) – формулой Лагранжа.
(9) Формула (8) наз остаточным членом ф-лы Тейлора в интегральной форме. Ф-ла (9) – формулой Лагранжа.
Преобразуя ф-лу Тейлора при х0 = 0 получаем ф-лу Маклорена.
Т3 Если ф-ция f(x) имеет в окрестности т х0 производные любого порядка и все они ограниченны одним и тем же числом С, т е " x Î U(x0) |f(n)(x)|<=C, то ряд Тейлора этой ф-ции сходится в ф-ции f(x) для всех х из этой окрестности.
№17
1 Формула ГринаСия очень полезная в сельском хозяйстве формула устанавливает связь между криволинейными и двойными интегралами.
Пусть имеется некоторая правильная замкнутая область Д, ограниченная контуром L и пущая ф-ции P(x,y) и Q(x,y) непрерывны вместе со своими частными производными: ![]() в данной области. тогда имеет место ф-ла:
в данной области. тогда имеет место ф-ла:
![]()
И вот вся эта фигулина и есть формула Грина.
Контур L определяющий область д может быть задан показательными уравнениями х = х1(у), х=х2(у) с<=y<=d x1(y)<=x2(y) или
y = y1(x), y=y2(x) a<=x<=b y1(x)<=y2(x).
Рассмотрим область Д ограниченную неравенствами: a<=x<=b и y1(x)<=y2(x). и преобразуем двойной интеграл ![]() к криволинейным для чего сведем его к повторному и ф-ле Невтона-Лыебница выполним интегрирование по у и получим:
к криволинейным для чего сведем его к повторному и ф-ле Невтона-Лыебница выполним интегрирование по у и получим:
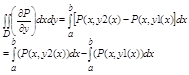 каждый из 2 определенных интегралов в правой части последнего равенства = криволинейному интегралу 2 рода взятому по соответствующей кривой а именно:
каждый из 2 определенных интегралов в правой части последнего равенства = криволинейному интегралу 2 рода взятому по соответствующей кривой а именно:

![]()
Итак двойной интеграл: ![]()
Формула Грина остается справедливой для всякой замкнутой области Д, которую можно разбить проведением дополнительных линий на конечной число правильных замкнутых областей.
2 Разложение элементарных ф-ций в ряд Тейлора (Маклорена)
1Разложение ф-ции ех
![]() ряд Маклорена.
ряд Маклорена.
радиус сходимости:
R=¥ следовательно ряд абсолютно сходится на всей числовой прямой.
2Разложение sinx и cosx В степенной ряд Маклорена
![]()
сходится на всей числовой оси
![]() сходится на всей числовой оси
сходится на всей числовой оси
3. f(x) = (1+x)a
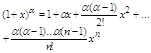
Наз. биномиальный ряд с показателем a Различают 2 случая:
1- a Î N, тогда при любом х все члены ф-лы исчезают, начиная с (a +2) поэтому ряд Маклорена содержит конечное число членов и сходится при всех х. Получается формула Бинома Невтона: ![]() , где
, где ![]() биномиальный коэффициент.
биномиальный коэффициент.
2- a Î R>N (a ¹ 0 х ¹ 0) и ряд сходится абсолютно при |x|>1
4 Разложение ф-ции ln(1+x)
![]()
сходится при –1<x<=1
5 Разложение arctgx в степенной ряд Маклорена
![]() сходится при -1<=x<=1
сходится при -1<=x<=1
№18
1 Некоторые приложения криволинейных интегралов 1 рода.
1.Интеграл![]() - длине дуги АВ
- длине дуги АВ
2.Механический смысл интеграла 1 рода.
Если f(x,y) = r(x,y) – линейная плотность материальной дуги, то ее масса: ![]()
для пространственной там буква зю добавляется.
3.Координаты центра масс материальной дуги:
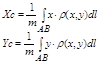
4. Момент инерции дуги лежащей в плоскости оху относительно начала координат и осей вращения ох, оу:
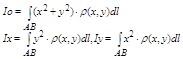
5. Геометрический смысл интеграла 1 рода
Пусть ф-ция z = f(x,y) – имеет размерность длины f(x,y)>=0 во всех точках материальной дуги лежащей в плоскости оху тогда:
![]() , где S – площадь цилиндрической поверхности, кот состоит из перпендикуляров плоскости оху, восст в точках М(x,y) кривой АВ.
, где S – площадь цилиндрической поверхности, кот состоит из перпендикуляров плоскости оху, восст в точках М(x,y) кривой АВ.
2 Геометрические и арифметические ряды.
№19
1 Некоторые приложения криволинейных интегралов 2 рода.
Вычисление площади плоской области Д с границей L
![]()
2.Работа силы. Пусть материальная т очка под действием силы перемещается вдоль непрерывной плоской кривой ВС, направясь от В к С, работа этой силы:
![]()
при пространственной кривой там исчо третья функция появитца для буквы зю.
2 Свойства сходящихся рядов
№20
1 Условия независимости криволинейного интеграла 2 рода от пути интегрирования.
Плоская область W наз односвязной если не имеет дыр. т. е. однородная.
Пусть ф-ция P(x,y) и Q(x,y)вместе со своими частными производными непрерывны в некоторой замкнутой, односвязной области W тогда следующие 4 условия эквиваленты, т. е. выполнение какого либо из них влечет остальные 3.
1. Для " замкнутой кусочногладкой кривой L в W значение криволинейного интеграла:
![]()
2. Для все т. А и т. В области W значение интеграла ![]()
не зависит от выбора пути интегрирования, целиком лежащего в W.
3. Выражение Pdx+Qdy представляет собой полный дифференциал некоторых функций определенных в W существует ф-ция E=c(х,у) опред в W такая, что dE = Pdx+Pdy
4. В области W ![]()
Отседова следовает, что условие 3 является необходимым и достаточным условием при котором интегралы 2 рода не зависят от выбора пути интегрирования.
0 комментариев