Навигация
Решение через матрицу, обратную к базисной
4. Решение через матрицу, обратную к базисной.
Оптимальное
решение двойственной
задачи можно
найти по формуле
![]() .
Как видно из
оптимальной
симплекс-таблицы,
.
Как видно из
оптимальной
симплекс-таблицы,
![]() .
Тогда
.
Тогда ![]() .
Соответственно,
.
Соответственно,
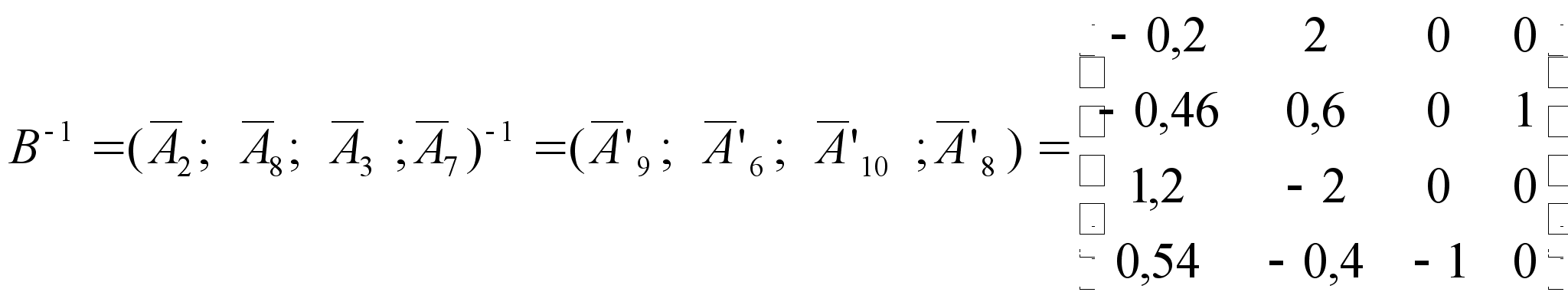 .
.
Получим:
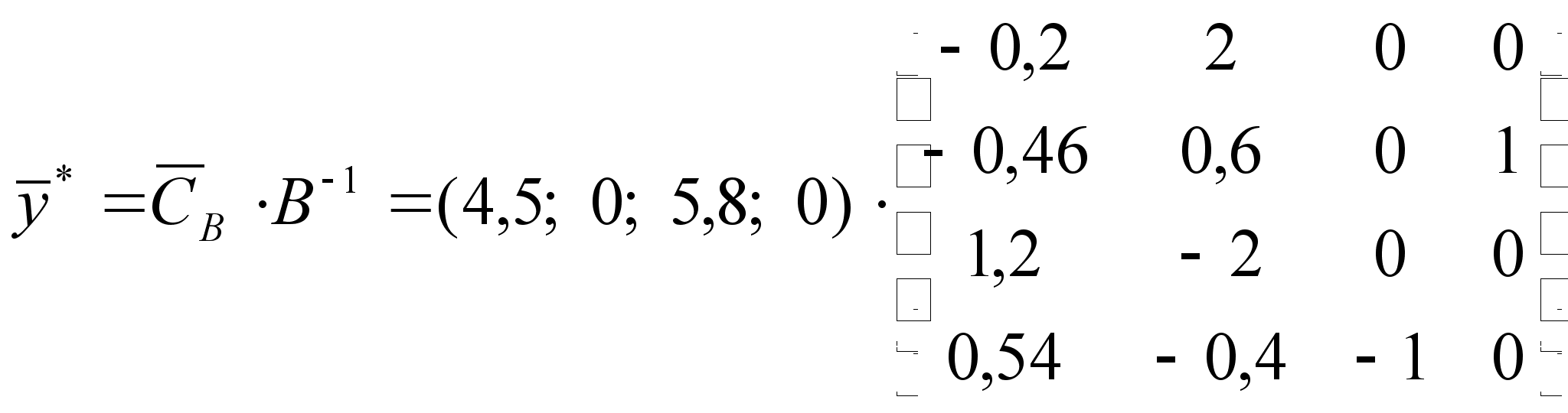 ,
,
Откуда ![]() .
.
Таким
образом, мы
видим, что всеми
четырьмя способами
было получено
одно и то же
решение: ![]() ;
;![]() .
.
Согласно первой теореме двойственности, если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план, причем значения функций цели при оптимальных планах равны между собой; если же целевая функция одной из задач неограниченна, то другая совсем не имеет планов, и наоборот.
В нашем случае пара задач имеет оптимальные планы, значения целевых функций при которых равны 5,28. Экономический смысл этого состоит в том, что в оптимальном плане минимальные затраты фирмы на производство тонны сплава равны максимальной прибыли некой другой фирмы от продажи первой фирме необходимых для производства ресурсов по условным ценам, равным двойственным оценкам этих ресурсов.
Как было
указано выше,
вторая теорема
двойственности
заключается
в выполнении
соотношений
дополняющей
нежесткости
в случае оптимальности
планов пары
задач (соотношения
(5) и (6)). Приведем
сначала экономическую
интерпретацию
условия (6). Каждому
из четырёх
"ресурсов"
исходной задачи
соответствует
его двойственная
оценка, или
условная цена
(![]() ,
,![]() ,
,![]() и
и ![]() соответственно).
В случае положительности
двойственной
оценки (в нашем
случае
соответственно).
В случае положительности
двойственной
оценки (в нашем
случае ![]() и
и ![]() )
справедливы
равенства
)
справедливы
равенства
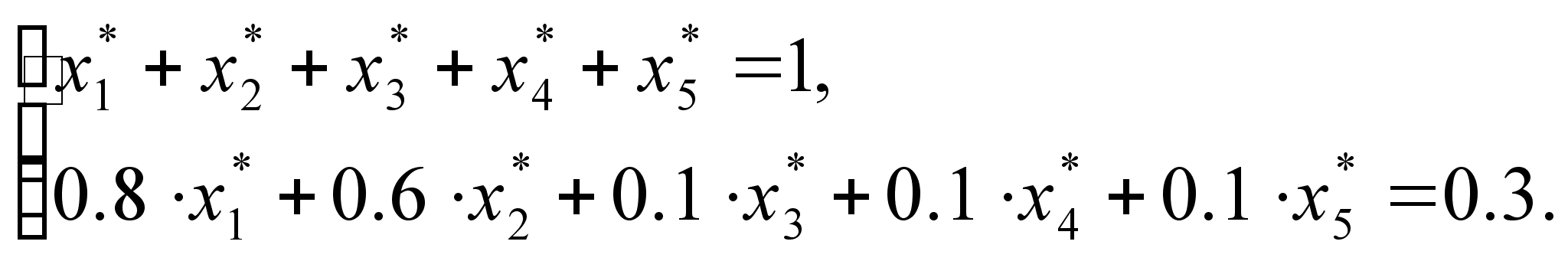 ,
,
т.е.
первый и второй
"ресурсы"
используются
полностью и
являются дефицитными.
Следует оговориться,
что первое
равенство
выполняется
всегда, в противном
случае задача
не имеет решения.
Это логически
понятно, поскольку
сумма частей
всегда равна
целому. Что
касается третьего
и четвёртого
ресурсов, то
они имеют нулевую
двойственную
оценку, т.е. эти
ресурсы не
является дефицитным.
Рассмотрим
теперь условие
(5). Поскольку ![]() ,
то справедливы
неравенства:
,
то справедливы
неравенства:
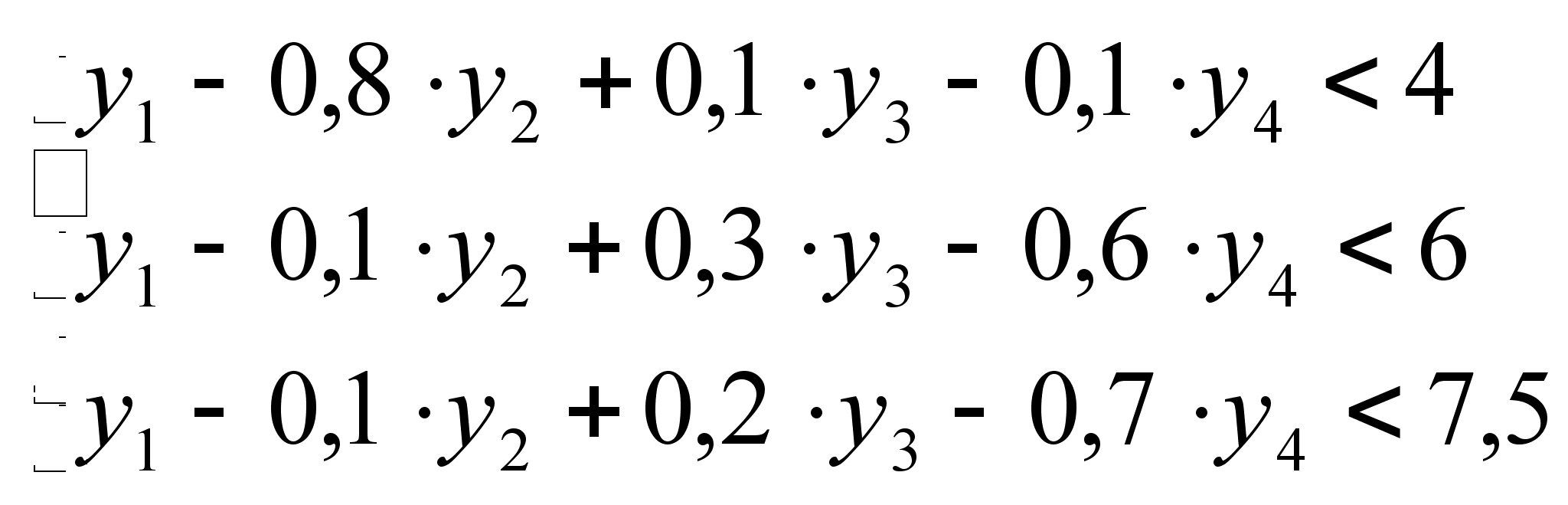 .
.
Экономически
это значит, что
затраты на
сырье №1, 4 и 5 превосходят
возможные
затраты в случае
закупки отдельных
ресурсов, поэтому
эти виды сырья
использоваться
не будут. С другой
стороны, ![]() ,
,![]() ,
следовательно,
,
следовательно,
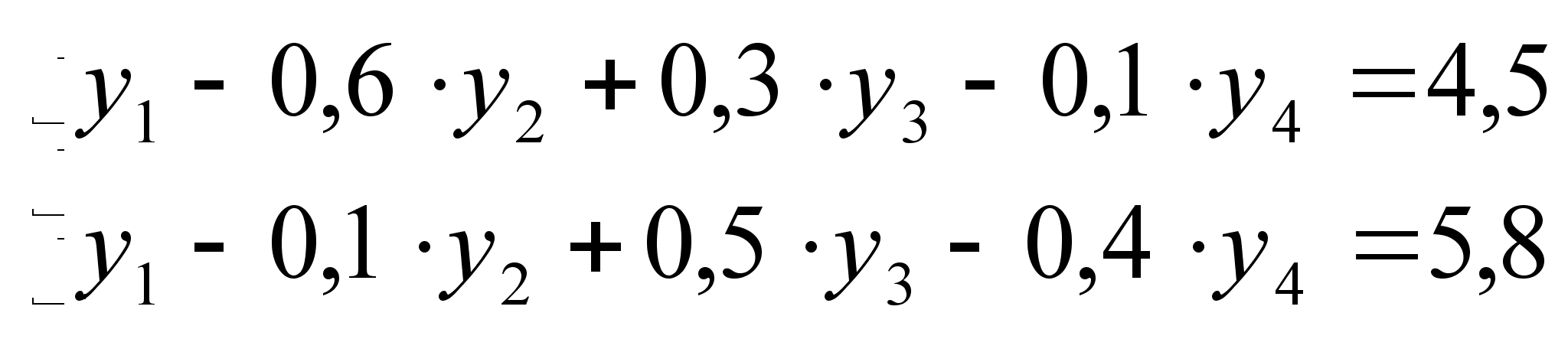
т.е. затраты на сырье первого и второго вида равны альтернативным затратам на производство, значит эти виды сырья будут использоваться.
Третья теорема
двойственности
позволяет
определить
зависимость
изменения
целевой функции
начальной
задачи от изменения
запасов "ресурсов":
 ,
т.е. в нашем случае
как изменяются
минимальные
издержки на
производство
единицы сплава
в зависимости
от изменения
"ресурсов".
Так, пусть, например,
максимальная
доля олова
увеличится
на 0,1, т.е. до 40 %. Тогда,
по третьей
теореме двойственности,
минимальные
издержки на
производство
единицы сплава
уменьшатся
на
,
т.е. в нашем случае
как изменяются
минимальные
издержки на
производство
единицы сплава
в зависимости
от изменения
"ресурсов".
Так, пусть, например,
максимальная
доля олова
увеличится
на 0,1, т.е. до 40 %. Тогда,
по третьей
теореме двойственности,
минимальные
издержки на
производство
единицы сплава
уменьшатся
на ![]() [у.е.].
С другой стороны,
изменение
минимальной
доли цинка или
свинца не приведет
к изменению
минимальных
издержек, поскольку
их двойственные
оценки равны
нулю. Но двойственные
оценки позволяют
о влиянии на
целевую функцию
не любых изменений
ресурсов, а
лишь таких,
какие не приводят
к недопустимости
оптимального
решения.
[у.е.].
С другой стороны,
изменение
минимальной
доли цинка или
свинца не приведет
к изменению
минимальных
издержек, поскольку
их двойственные
оценки равны
нулю. Но двойственные
оценки позволяют
о влиянии на
целевую функцию
не любых изменений
ресурсов, а
лишь таких,
какие не приводят
к недопустимости
оптимального
решения.
7
Лабораторная работа № 4
Телешовой Елизаветы, гр. 726,
Послеоптимизационный анализ задач линейного программирования. 1.Анализ чувствительности оптимального решения задачи к изменению свободных членов ограничений.Для изготовления определенного сплава из свинца, цинка и олова используется сырье из тех же металлов, отличающееся составом и стоимостью.
| Сырье | Содержание в процентах | ||||
| Компоненты | 1 | 2 | 3 | 4 | 5 |
| Свинец | 10 | 10 | 40 | 60 | 70 |
| Цинк | 10 | 30 | 50 | 30 | 20 |
| Олово | 80 | 60 | 10 | 10 | 10 |
| Стоимость, у. Е. | 4 | 4,5 | 5,8 | 6 | 7,5 |
Определить, сколько нужно взять сырья каждого вида, чтобы изготовить с минимальной себестоимостью сплав, содержащий олова не более 30%, цинка не менее 10%, свинца не более 40%.
Математическая модель:
Пусть хi – доля сырья i-го вида в единице полученного сплава. Тогда функция цели (себестоимость единицы сплава в у.е.) запишется следующим образом:
![]() .
.
Система ограничений будет иметь вид:

Запишем систему в каноническом виде:
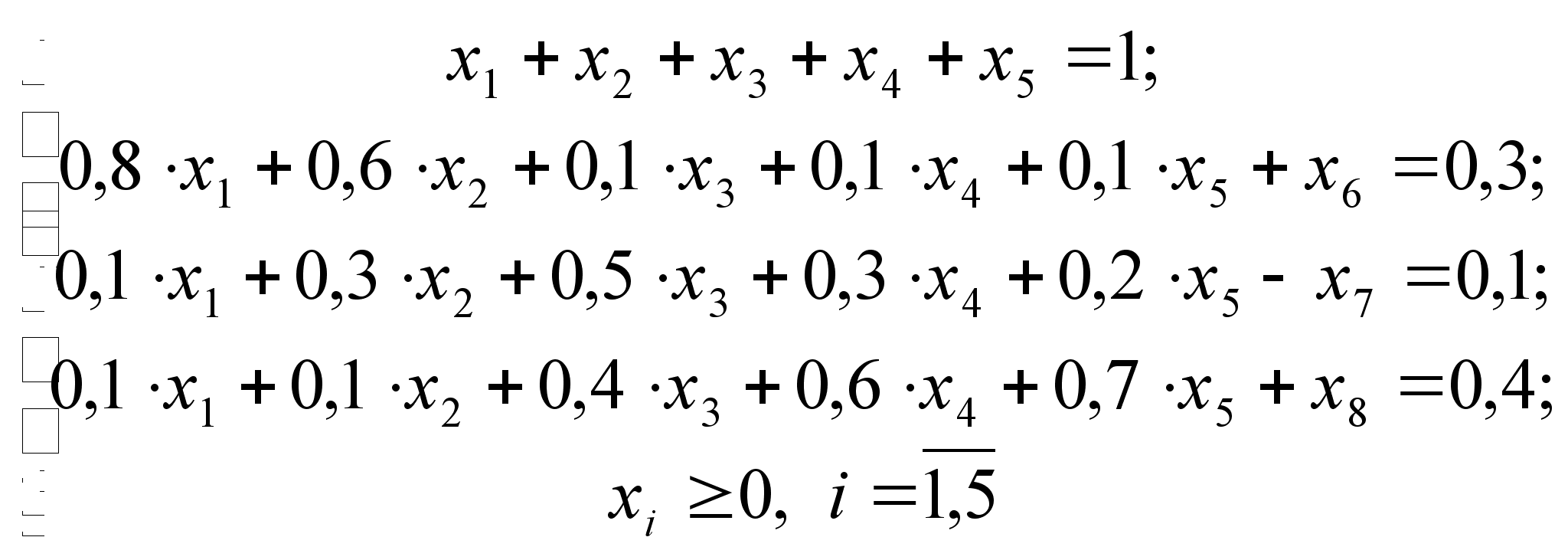
Оптимальная симплекс-таблица:
| 4 | 4,5 | 5,8 | 6 | 7,5 | 0 | 0 | 0 | M | M | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | В |
| 4,5 | X2 | 1,4 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | -0,2 | 0 | 0,4 |
| 0 | X8 | 0,12 | 0 | 0 | 0,2 | 0,3 | 0,6 | 0 | 1 | -0,46 | 0 | 0,12 |
| 5,8 | X3 | -0,4 | 0 | 1 | 1 | 1 | -2 | 0 | 0 | 1,2 | 0 | 0,6 |
| 0 | X7 | 0,12 | 0 | 0 | 0,2 | 0,3 | -0,4 | 1 | 0 | 0,54 | -1 | 0,32 |
| F | -0,02 | 0 | 0 | -0,2 | -1,7 | -2,6 | 0 | 0 | -6,06 | 0 | 5,28 | |
Оптимальное
решение: ![]() и оптимальное
значение целевой
функции:
и оптимальное
значение целевой
функции: ![]() .
.
Экономически
полученное
решение интерпретируется
следующим
образом: для
получения
единицы сплава
минимальной
себестоимости
необходимо
взять 40% сырья
№2 и 60% сырья №3.
При этом сплав
содержит ровно
30% олова, более
20% (точнее, 42%) цинка
и менее 40% (28%) свинца.
Минимальная
себестоимость
единицы сплава
составляет
5,28 у.е. Оптимальные
двойственные
оценки ![]() .
.
Теперь найдём область устойчивости двойственных оценок к изменению свободных членов ограничений. Как известно, область устойчивости двойственных оценок – это область изменения свободных членов ограничений, при которой двойственные оценки не меняются. Неизменность двойственных оценок говорит о том, что не меняют своих номеров базисные и свободные переменные в решении.
В связи с
вычислением
интервалов
устойчивости
необходимо
сделать замечание
о знаках неравенств.
Мы помним, что
изначально
их изменение
мы учитывали
(< на >), но знаки
самих неравенств
не меняли. Сейчас
мы также не
будем менять
знаки второго
и четвёртого
неравенств,
но примем во
внимание обратный
знак ![]() при расчёте
конкретных
значений. (Это
делается для
более наглядной
экономической
интерпретации
интервалов
устойчивости.)
при расчёте
конкретных
значений. (Это
делается для
более наглядной
экономической
интерпретации
интервалов
устойчивости.)
Пусть свободные
члены изменились
на ![]() ,
,![]() ,
,![]() и
и ![]() соответственно.
Тогда оптимальное
решение новой
задачи (базисные
компоненты)
можно найти
как:
соответственно.
Тогда оптимальное
решение новой
задачи (базисные
компоненты)
можно найти
как:
![]() .
.
Базисное решение вычисляется через матрицу, обратную к базисной, и свободные члены ограничений. Из оптимальной симплекс-таблицы получим матрицу, обратную к базисной, и оптимальное решение (базисные компоненты):
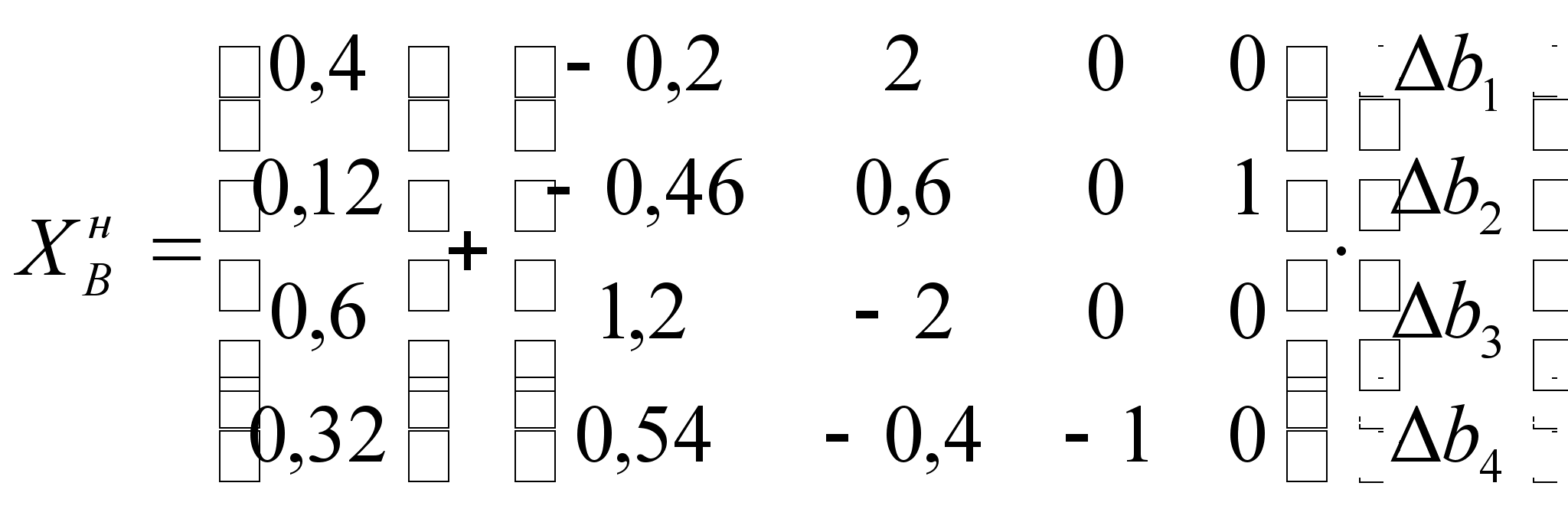 =>
=>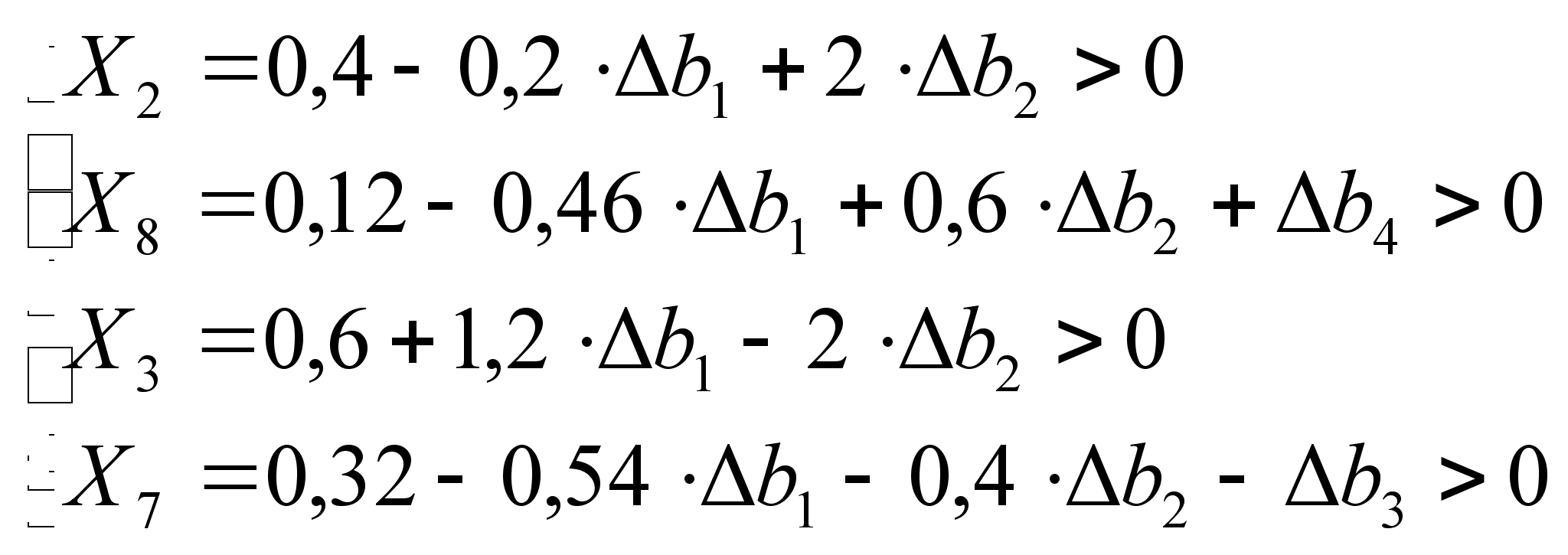
Все элементы решения должны быть неотрицательны, иначе решение будет недопустимым, т.е. базисное решение остаётся оптимальным до тех пор, пока оно допустимое. Область устойчивости следующая:
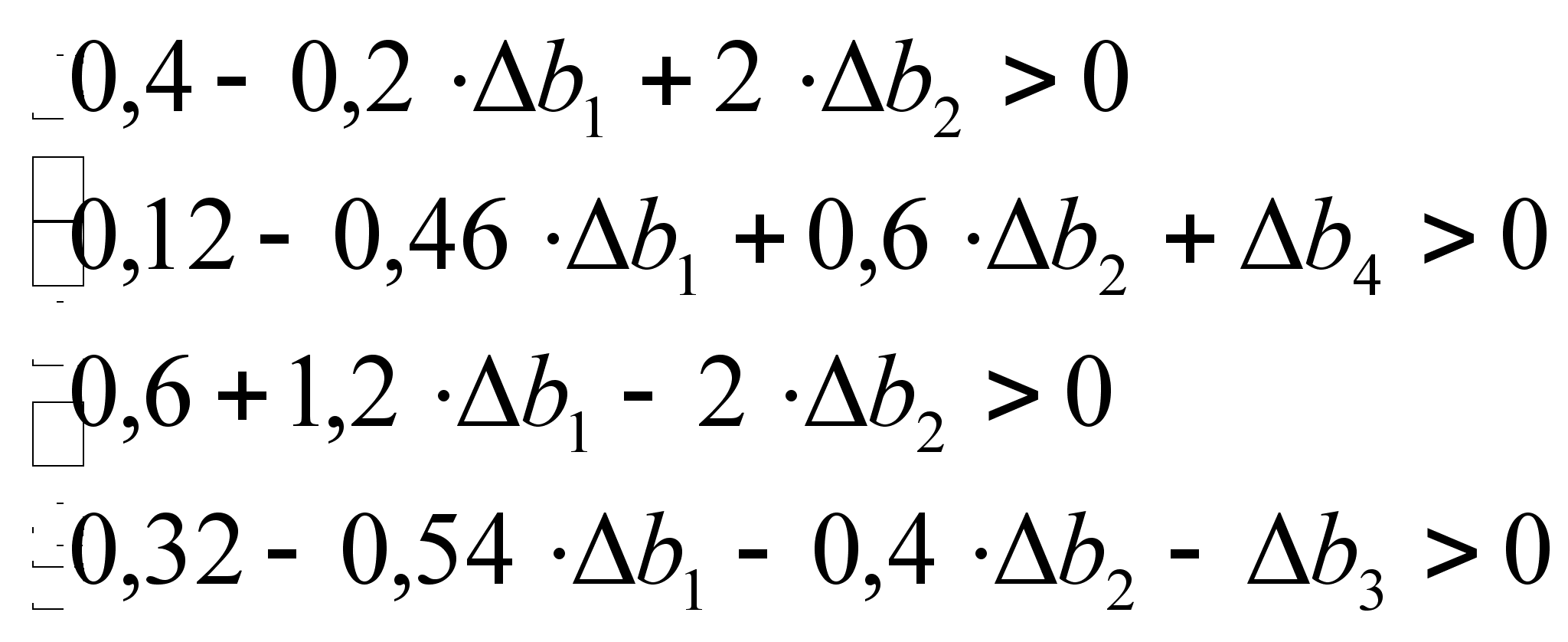 .
.
Теперь найдём интервалы устойчивости (интервал устойчивости двойственных оценок к изменению правой части ограничения или i-го ресурса – такое множество i–го ресурса, при котором двойственные оценки не меняются):
1)![]() ,
,![]() :
:
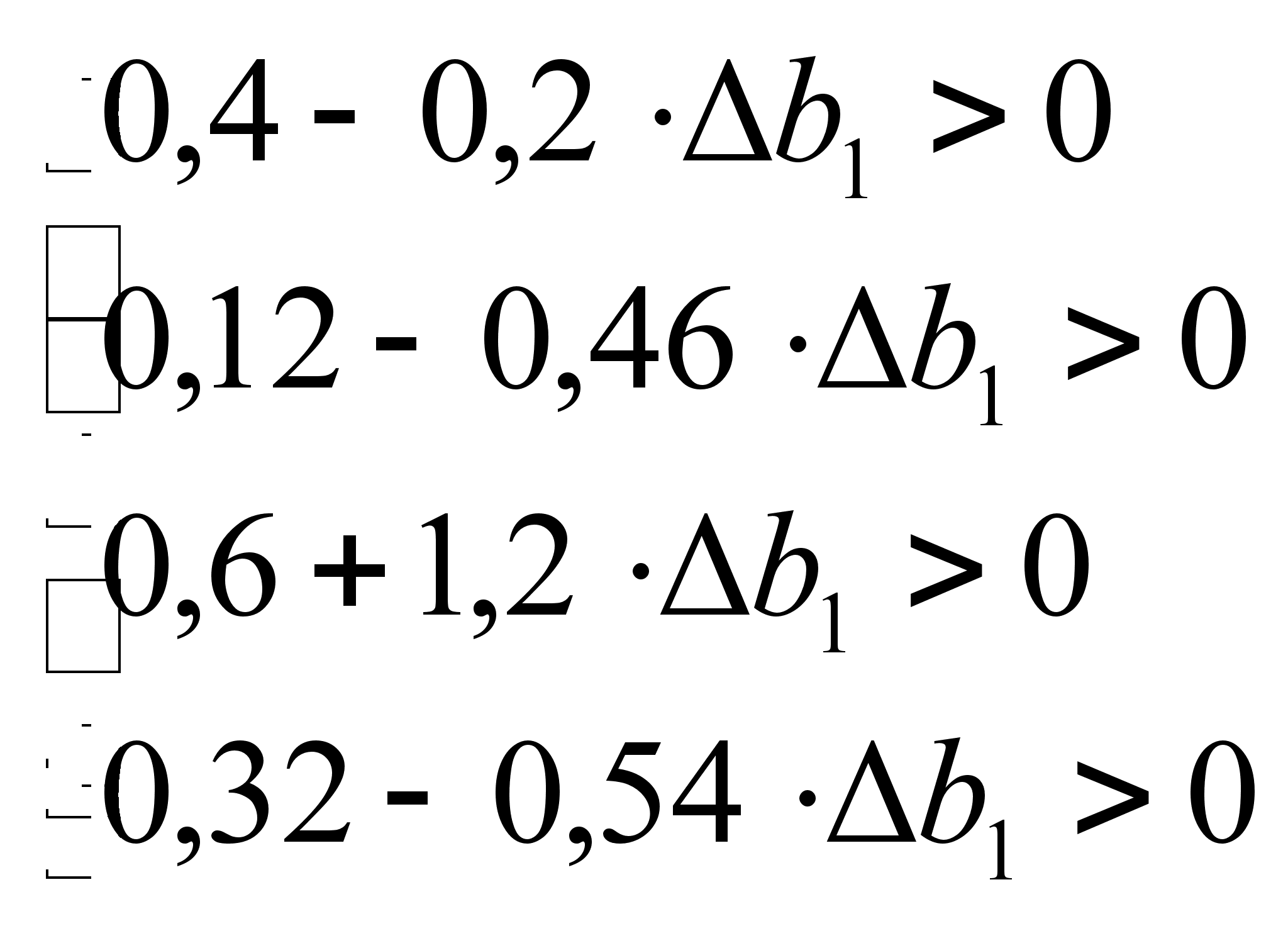 =>
=> ![]() ,
,![]()
2)![]() ,
,![]() :
:
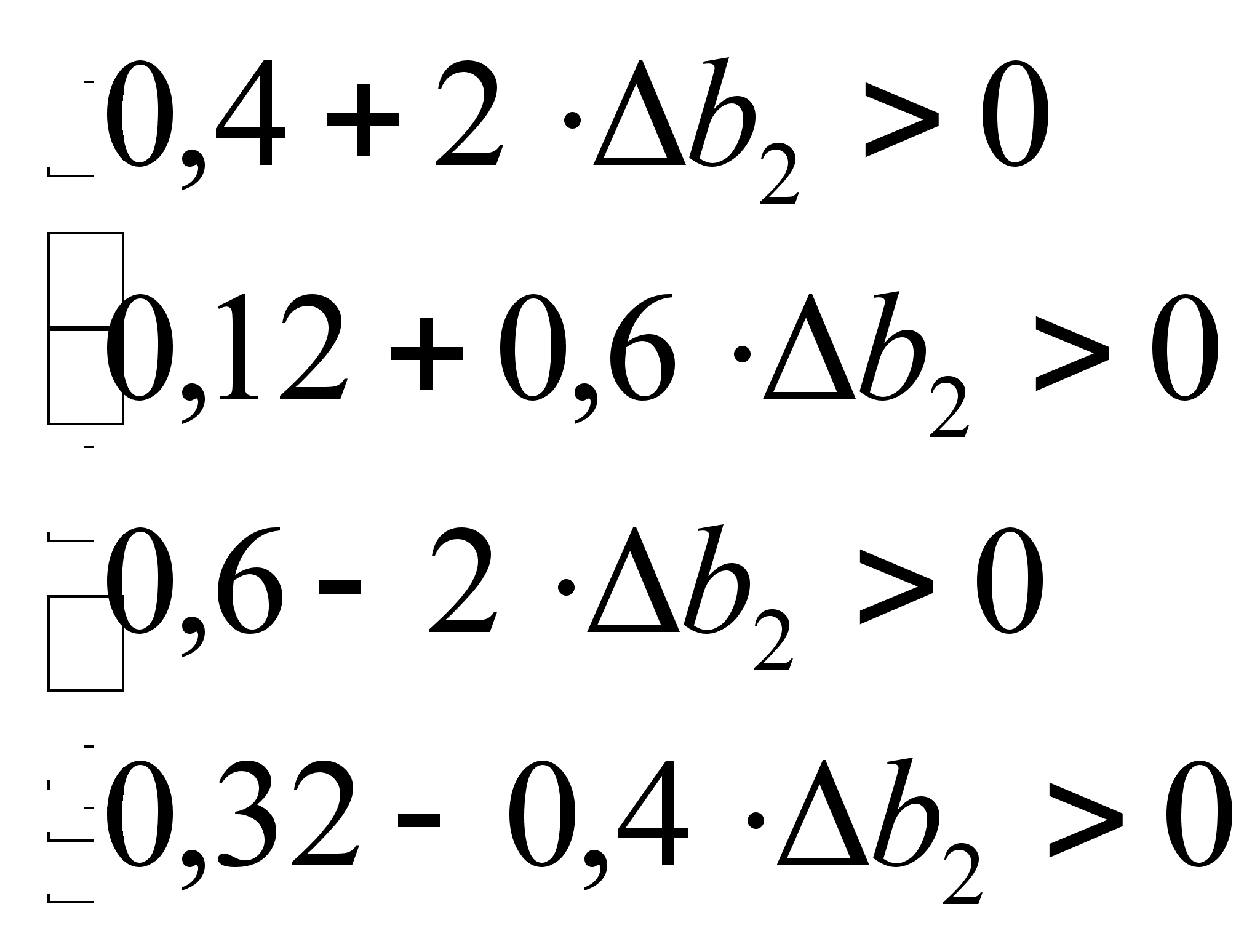 =>
=> ![]() ,
,![]()
3)![]() ,
,![]() :
:
![]() =>
=> ![]() ,
,![]() .
.
4)![]() ,
,![]() :
:
![]() =>
=> ![]() ,
,![]() .
.
Полученные
результаты
экономически
означают, что
свободный член
в первом ограничении
может меняться
от 0,5 до 1,26,
но экономического
смысла это ни
какого не имеет,
т.к. сумма составляющих
долей сплава
всегда 100%. Содержание
олова в новом
сплаве варьируется
от 10%
до 60%,
цинка – от нуля
(![]() не имеет экономической
интерпретации)
до 42%
и свинца – от
28%
до 100% (аналогично
случаю с цинком
не имеет экономической
интерпретации)
до 42%
и свинца – от
28%
до 100% (аналогично
случаю с цинком
![]() не может быть
объяснена
экономически).
Возможны также
различные
комбинации
изменений,
которые описывает
область устойчивости
(интервалы
устойчивости
являются
своеобразными
частными случаями
области устойчивости).
При данных
изменениях
ресурсов двойственные
оценки не изменятся,
а значит
и номера
базисных переменных
также не изменятся.
не может быть
объяснена
экономически).
Возможны также
различные
комбинации
изменений,
которые описывает
область устойчивости
(интервалы
устойчивости
являются
своеобразными
частными случаями
области устойчивости).
При данных
изменениях
ресурсов двойственные
оценки не изменятся,
а значит
и номера
базисных переменных
также не изменятся.
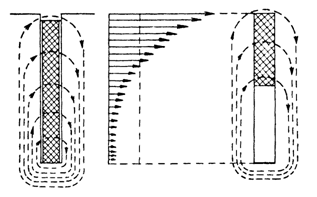
И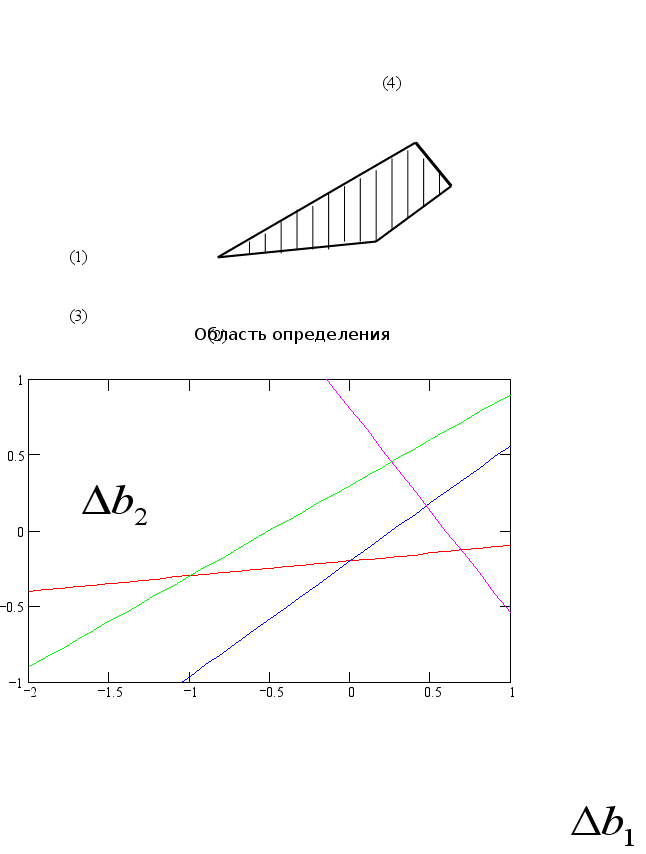
зобразим
область устойчивости
двойственных
оценок к изменению
свободных
членов ограничений
графически.
Для этого, исходя
из экономических
соображений
и наглядности
графика, построим
его в координатах
![]() и
и ![]() ,
т.е.
,
т.е. ![]() .
Получим:
.
Получим:
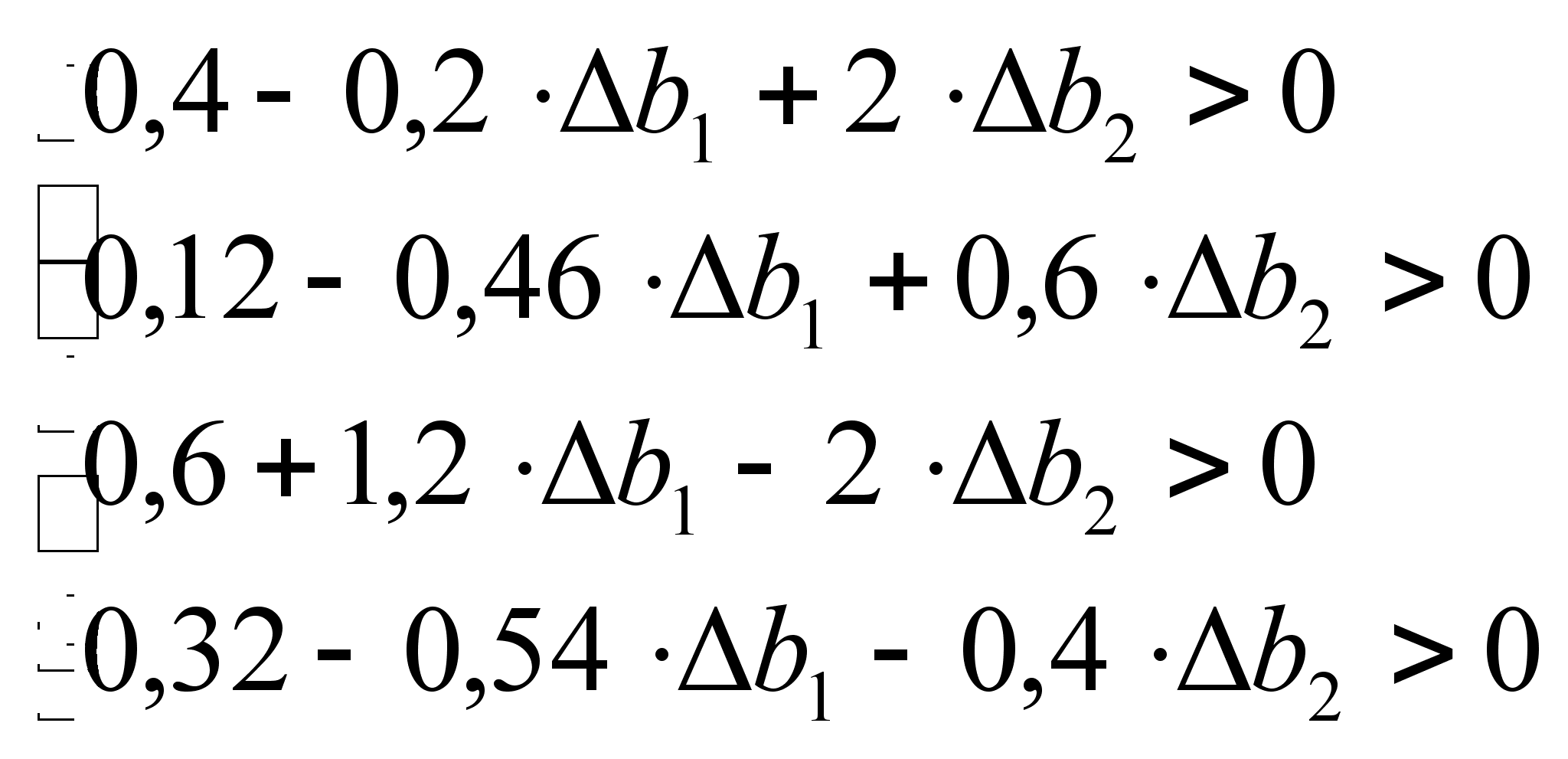
![]()
Пример практического применения интервалов устойчивости.
Изменим условие задачи следующим образом:
а) содержание олова в новом сплаве не должно превосходить 15%;
Интервал
устойчивости
для олова – это ![]() .
15% или 0,15 входят
в этот интервал,
следовательно
двойственные
оценки не изменятся
и оптимальное
решение будет
(при
.
15% или 0,15 входят
в этот интервал,
следовательно
двойственные
оценки не изменятся
и оптимальное
решение будет
(при ![]() ).
).
 .
.
По третьей теореме двойственности найдём значение критерия при этом решении:
![]() =>
=> ![]() .
.
б) содержание цинка должно быть не менее 45%;
Интервал
устойчивости
для цинка - ![]() .
Т.к. содержание
цинка в сплаве
должно быть
не более 42%, а т.к.
0,45 не входит в
интервал устойчивости
двойственных
оценок, то
двойственные
оценки и номера
базисных переменных
сменятся (
.
Т.к. содержание
цинка в сплаве
должно быть
не более 42%, а т.к.
0,45 не входит в
интервал устойчивости
двойственных
оценок, то
двойственные
оценки и номера
базисных переменных
сменятся (![]() ).
).
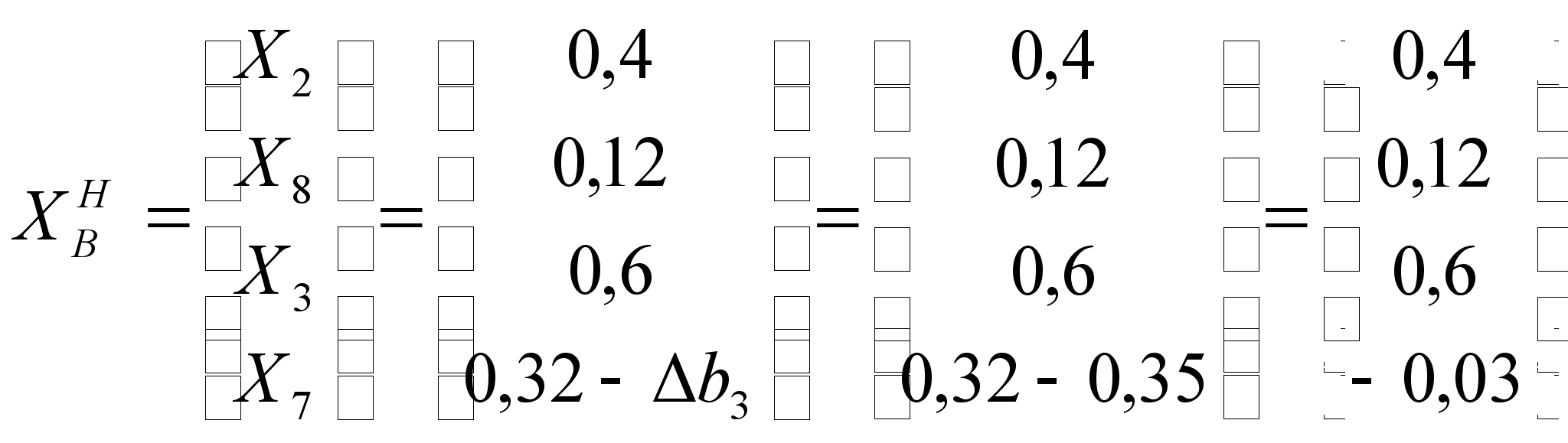 .
.
Решение недопустимое. Но если бы оно было допустимым, то оно было бы и оптимальным, а значит, оценки бы удовлетворяли критерию оптимальности. Полученное решение является псевдопланом и можно использовать двойственный симплекс-метод.
| 4 | 4,5 | 5,8 | 6 | 7,5 | 0 | 0 | 0 | 0 | 0 | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | В |
| 4,5 | X2 | 1,4 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | -0,2 | 0 | 0,4 |
| 0 | X8 | 0,12 | 0 | 0 | 0,2 | 0,3 | 0,6 | 0 | 1 | -0,46 | 0 | 0,12 |
| 5,8 | X3 | -0,4 | 0 | 1 | 1 | 1 | -2 | 0 | 0 | 1,2 | 0 | 0,6 |
| 0 | X7 | 0,12 | 0 | 0 | 0,2 | 0,3 | -0,4 | 1 | 0 | 0,54 | -1 | -0,03 |
| F | -0,02 | 0 | 0 | -0,2 | -1,7 | -2,6 | 0 | 0 | -6,06 | 0 | 5,28 | |
Определим,
какую из переменных
выведем из
базиса. В данном
случае это
будет единственная
отрицательная
переменная
![]() .
Введём в базис
одну из свободных
переменных,
у которой коэффициент
разрешающей
строки отрицателен.
Разрешающий
столбец выбирается
по минимальному
по модулю отношению
оценок к отрицательным
коэффициентам
разрешающей
строки. Переменой,
вводимой в
базис будет
.
Введём в базис
одну из свободных
переменных,
у которой коэффициент
разрешающей
строки отрицателен.
Разрешающий
столбец выбирается
по минимальному
по модулю отношению
оценок к отрицательным
коэффициентам
разрешающей
строки. Переменой,
вводимой в
базис будет
![]() .
После стандартных
преобразований
однократного
замещения
получим новую
симплекс-таблицу:
.
После стандартных
преобразований
однократного
замещения
получим новую
симплекс-таблицу:
| 4 | 4,5 | 5,8 | 6 | 7,5 | 0 | 0 | 0 | 0 | 0 | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | В |
| 4,5 | X2 | 2 | 1 | 0 | 1 | 1,5 | 0 | 5 | 0 | 2,5 | -5 | 0,25 |
| 0 | X8 | 0,3 | 0 | 0 | 0,5 | 0,75 | 0 | 1,5 | 1 | 0,35 | -1,5 | 0,075 |
| 5,8 | X3 | -1 | 0 | 1 | 0 | -0,5 | 0 | -5 | 0 | -1,5 | 5 | 0,75 |
| 0 | X6 | -0,3 | 0 | 0 | -0,5 | -0,75 | 1 | -2,5 | 0 | -1,35 | 2,5 | 0,075 |
| F | -0,8 | 0 | 0 | -1,5 | -3,65 | 0 | -6,5 | 0 | 2,55 | 6,5 | 5,475 | |
Как видим,
оценки по-прежнему
удовлетворяют
критерию
оптимальности
и все базисные
переменные
неотрицательны,
значит, решение
допустимое
и оптимальное.
Новое решение
задачи ![]() .
Оптимальное
значение критерия
.
Оптимальное
значение критерия
![]() .
Это означает,
что для производства
единицы сплава
необходимо
взять 25% второго
сырья и 75% третьего
сырья. При этом
доля цинка в
новом сплаве
будет ровно
45%, олова 22,5% и свинца
32,5%. Минимальная
стоимость тонны
сплава будет
5,475 у.е.
.
Это означает,
что для производства
единицы сплава
необходимо
взять 25% второго
сырья и 75% третьего
сырья. При этом
доля цинка в
новом сплаве
будет ровно
45%, олова 22,5% и свинца
32,5%. Минимальная
стоимость тонны
сплава будет
5,475 у.е.
в) в новом сплаве должно быть менее 40% олова и более 30% цинка;
Запишем
область устойчивости
двойственных
оценок, учитывая
новые изменения
(![]() ;
;
![]() ):
):
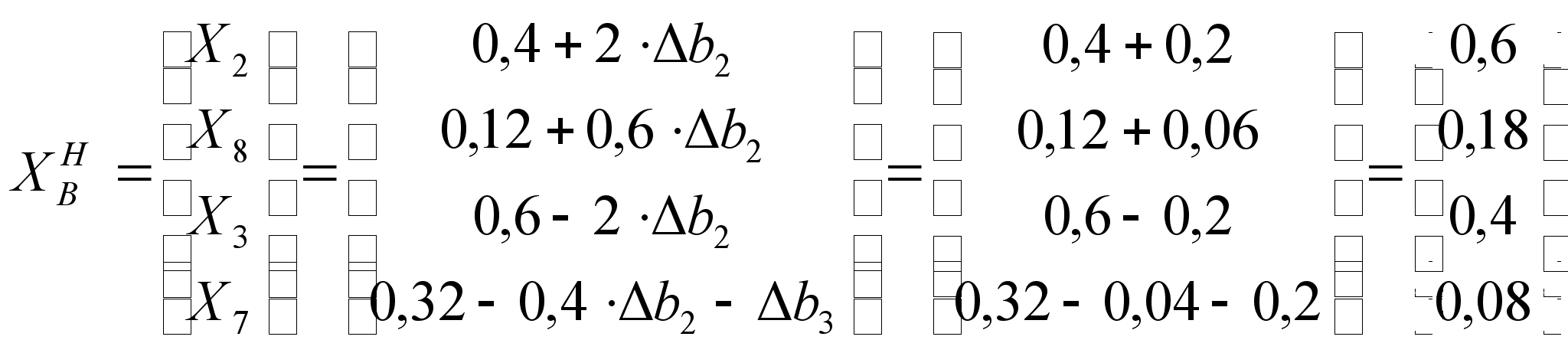 .
.
Решение является допустимым, а значит, и оптимальным. Значение критерия найдём по третьей теореме двойственности:
![]() =>
=> ![]()
г) менее 60% олова и более 40% цинка;
В данном
случае изменения
составляют:
увеличение
содержания
олова на 30% и цинка
на 30%, т.е ![]() и
и ![]() .
Поэтому
.
Поэтому
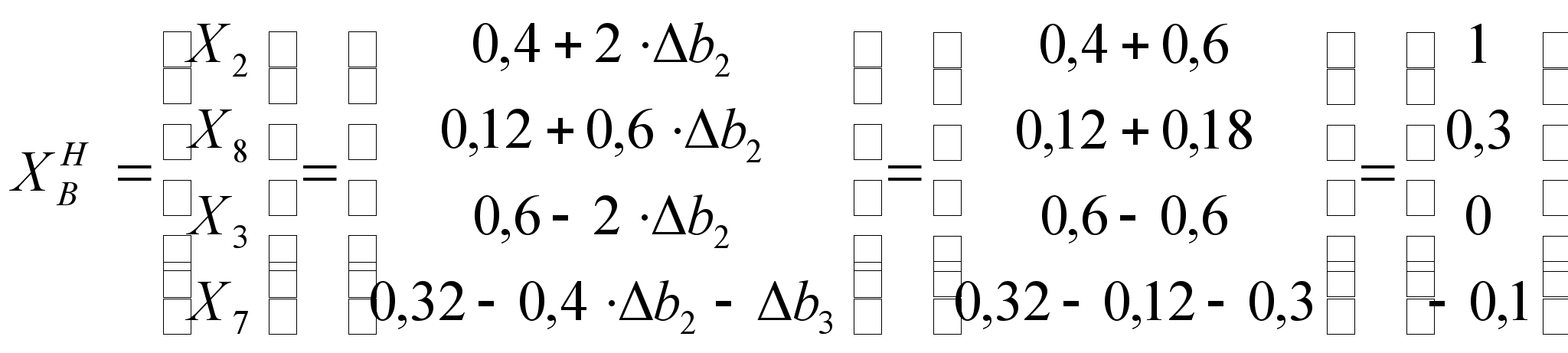
Решение недопустимое, но является псевдопланом, поэтому, руководствуясь рассуждениями, аналогичными пункту б), решим задачу двойственным симплекс-методом.
| 4 | 4,5 | 5,8 | 6 | 7,5 | 0 | 0 | 0 | 0 | 0 | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | В |
| 4,5 | X2 | 1,4 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | -0,2 | 0 | 0,4 |
| 0 | X8 | 0,12 | 0 | 0 | 0,2 | 0,3 | 0,6 | 0 | 1 | -0,46 | 0 | 0,12 |
| 5,8 | X3 | -0,4 | 0 | 1 | 1 | 1 | -2 | 0 | 0 | 1,2 | 0 | 0,6 |
| 0 | X7 | 0,12 | 0 | 0 | 0,2 | 0,3 | -0,4 | 1 | 0 | 0,54 | -1 | -0,1 |
| F | -0,02 | 0 | 0 | -0,2 | -1,7 | -2,6 | 0 | 0 | -6,06 | 0 | 5,28 | |
Оптимальная симплекс-таблица:
| 4 | 4,5 | 5,8 | 6 | 7,5 | 0 | 0 | 0 | 0 | 0 | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | В |
| 4,5 | X2 | 2 | 1 | 0 | 1 | 1,5 | 0 | 5 | 0 | 2,5 | -5 | 0.5 |
| 0 | X8 | 0,3 | 0 | 0 | 0,5 | 0,75 | 0 | 1,5 | 1 | 0,35 | -1,5 | 0,15 |
| 5,8 | X3 | -1 | 0 | 1 | 0 | -0,5 | 0 | -5 | 0 | -1,5 | 5 | 0,5 |
| 0 | X6 | -0,3 | 0 | 0 | -0,5 | -0.75 | 1 | -2.5 | 0 | -1.35 | 2,5 | 0,25 |
| F | -0,8 | 0 | 0 | -1,5 | -3,65 | 0 | -6,5 | 0 | 2,55 | 6,5 | 5,15 | |
Получим
следующее
решение: ![]() ,
,
![]() .
Таким образом,
для изготовления
нового сплава
необходимо
взять 50%
сырья №2
и 50% сырья
№3.
.
Таким образом,
для изготовления
нового сплава
необходимо
взять 50%
сырья №2
и 50% сырья
№3.
Задача анализа дополнительно закупаемых объёмов ресурсов с целью обеспечения наибольшей эффективности планирования.
Предположим, что появилась возможность покупать сырьё у других поставщиков по более низкой цене: цинк по 2 у.е., а за олово и свинец, т.к. согласно экономическому смыслу задачи они являются "антиблагами", мы получаем большую доплату от их поставщика: 1,5 у.е. и 0,5 у.е. соответственно. Руководитель предприятия выделил на закупку ресурсов 3 у.е.
Решение:
По ранее
полученным
результатам
мы знаем, что
предприятие
тратит минимум
средств (5,28 у.е.)
когда в полученном
сплаве ровно
30% олова, 42% цинка
и 28% свинца (будем
считать для
удобства, что
для производства
10 тонн сплава
необходимо
3 тонны олова,
4,2 тонны цинка
и 2,8 тонн свинца).
Т.к. олово и свинец
мы получаем
с доплатой, то
возьмём их в
полном объёме,
необходимом
для производства
сплава. От "покупки"
олова мы получим
![]() ,
а от свинца –
,
а от свинца –
![]() ,
т.е. всего 5,9 у.е.
(в связи с их
доходностью,
а не убыточностью
временно исключим
их из рассмотрения).
,
т.е. всего 5,9 у.е.
(в связи с их
доходностью,
а не убыточностью
временно исключим
их из рассмотрения).
Будем вести
анализ закупок
цинка. На первой
итерации мы
не закупаем
цинк, т.к. в этом
случае он бы
приносил больше
убытка (двойственная
оценка равна
нулю по сравнению
с предлагаемой
ценой в 2 у.е.).
Решив новую
задачу без
производства
олова и свинца,
мы безусловно
выйдем за границы
области устойчивости
двойственных
оценок. Кроме
того, сменится
решение: двойственная
оценка цинка
увеличится
до 3 и новое значение
целевой функции
понизится до
4 у.е. Вычтем из
этих затрат
на производство
сплава доход
от получения
олова и цинка:
![]() .
Это значит, что
на производство
сплава мы не
только не тратим
средств, но и
получаем прибыль
1,9 у.е.
.
Это значит, что
на производство
сплава мы не
только не тратим
средств, но и
получаем прибыль
1,9 у.е.
С увеличением двойственной оценки цинка становится выгодно покупать его. Но мы располагаем суммой денег только 3 у.е. и можем закупить на них 1,5 тонн вместо 2 необходимых. Теперь нам нужно производить только 0,5 тонны цинка. На второй итерации мы получаем такое же решение: критерий равен 4 у.е. и двойственная оценка цинка, которого мы производим 3 тонны, равна 4.
Таким образом, мы получили оптимальное решение расходования выделенных 3 у.е.: "закупать" с доплатой 4 тонны олова и 5 тонн свинца и покупать по цене 2 у.е. 1,5 тонны цинка. При таком плане предприятие получит прибыль от производства сплава в размере 1,9 у.е.
2.Анализ чувствительности оптимального решения задачи к изменению коэффициентов целевой функции.Определим интервал устойчивости решения к изменению стоимости сырья, то есть, в каких пределах могут меняться цены на сырьё, чтобы план выпуска сплава не изменился. Для этого рассмотрим два случая: изменение цен (коэффициентов целевой функции) происходит на сырьё, использующееся при производстве сплава (базисные переменные) и не использующееся (свободные переменные).
Похожие работы
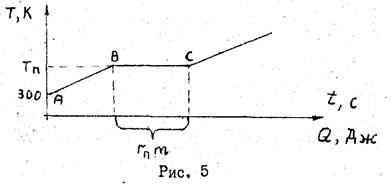
... изменение. 3. Что такое термодинамическая вероятность состояния (статистический вес). 4. Статистический смысл изменения энтропии. 5. Первый закон термодинамики. 6. Вывод рабочей формулы (36) данной работы. 7. Второй закон термодинамики и его статистический смысл. 6. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ И УДЕЛЬНОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ МЕТАЛЛА Цель работы Исследовать фазовый переход первого рода ...
... , выражать свою позицию, рефлексировать собственное поведение, самостоятельно принимать решения и т.п.» [20, с.351]. Именно такие ситуации возможно создавать при проведении лабораторного практикума. Студент, выполняя самостоятельно творческое задание исследовательского характера, проходит от начала до конца путь исследователя, решающего реальную научную проблему. Пройдя такой путь несколько раз ...
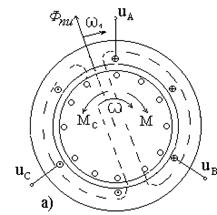
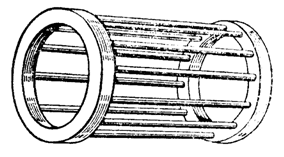
... концентрических окружностей с уменьшающимся радиусом по мере затухания колебаний скорости и момента. Аналогичная картина наблюдается при ступенчатом набросе нагрузки. 5. РАЗРАБОТКА ВИРТУАЛЬНОЙ ЛАБОРАТОРНОЙ РАБОТЫ НА БАЗЕ ВИРТУАЛЬНОЙ АСИНХРОННОЙ МАШИНЫ Иную возможность анализа АД представляет специализированный раздел по электротехнике Toolbox Power System Block. В его библиотеке имеются блоки ...
... Р- 122”.- Техническое описание. 3 “Техника чтения схем автоматического управления и технологического контроля”. – Энергоатомиздат, 1991.4 ДОКЛАД “Проект лабораторного стенда по изучению частотного электропривода на базе автономного инвертора напряжения фирмы OMRON”. В настоящее время на АО “Северсталь” происходит активное внедрение частотных преобразователей. Это объясняется тем, что частотное ...

0 комментариев