Навигация
Предположим, что теорема доказана для любого k < s и что φ содержит s логических связок и кванторов
2. Предположим, что теорема доказана для любого k < s и что φ содержит s логических связок и кванторов.
(a)
φ есть
![]() ψ.
По индуктивному
предположению,
существует
класс W
такой, что
ψ.
По индуктивному
предположению,
существует
класс W
такой, что
![]() x1…
x1…![]() xn
(
xn
(![]()
![]() W
W ![]() ψ (x1,…,xn,
Y1,…,
Ym)).
ψ (x1,…,xn,
Y1,…,
Ym)).
Теперь остается
положить
Z = ![]() .
.
(b)
φ есть
ψ ![]() θ.
По индуктивному
предположению,
существуют
классы Z1
и Z2
такие, что
θ.
По индуктивному
предположению,
существуют
классы Z1
и Z2
такие, что
![]() x1…
x1…![]() xn
(
xn
(![]()
![]() Z1
Z1
![]() ψ
(x1,…,xn,
Y1,…,
Ym))
и
ψ
(x1,…,xn,
Y1,…,
Ym))
и
![]() x1…
x1…![]() xn
(
xn
(![]()
![]() Z2
Z2
![]() θ
(x1,…,xn,
Y1,…,
Ym)).
θ
(x1,…,xn,
Y1,…,
Ym)).
Искомым
классом Z в этом случае
будет класс
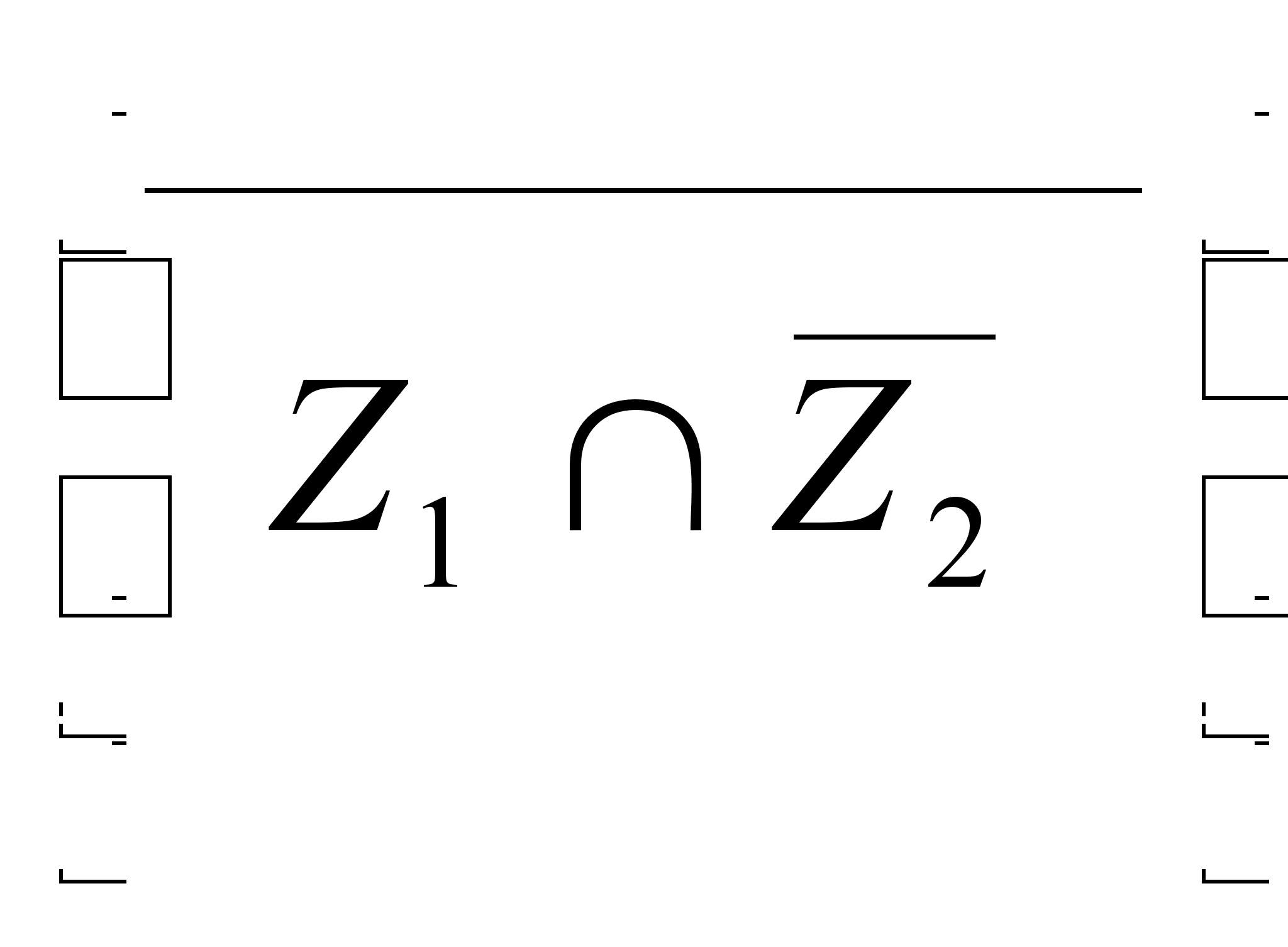 .
.
(c)
φ есть ![]() x
ψ. По индуктивному
предположению,
существует
класс W
такой, что
x
ψ. По индуктивному
предположению,
существует
класс W
такой, что
![]() x1…
x1…![]() xn
xn![]() x
(
x
(![]()
![]() W
W![]() ψ (x1,…,
xn,
x,
Y1,…,
Ym)).
ψ (x1,…,
xn,
x,
Y1,…,
Ym)).
Применим сперва
![]()
![]() X
X![]() Z
Z ![]() x1
…
x1
… ![]() xn
(
xn
(![]()
![]() Z
Z![]()
![]() y
(
y
(![]()
![]() X)).
X)).
при X
= ![]() и получим класс
Z1
такой, что
и получим класс
Z1
такой, что
![]() x1
…
x1
… ![]() xn
(
xn
(![]()
![]() Z1
Z1![]()
![]() x
x![]() ψ
(x1,…,
xn,
x, Y1,…,
Ym)).
ψ
(x1,…,
xn,
x, Y1,…,
Ym)).
Теперь положим
окончательно
Z
= ![]() ,
замечая, что
,
замечая, что ![]() x
ψ эквивалентно
x
ψ эквивалентно
![]()
![]() x
x![]() ψ.
ψ.
Примеры. 1.
Пусть φ
(X,
Y1,
Y2)
есть формула ![]() u
u![]() v
(X
=
v
(X
= ![]() & u
& u ![]()
![]() Y1
& v
Y1
& v ![]() Y2).
Здесь кванторы
связывают
только переменные
для множеств.
Поэтому, в силу
теоремы о
существовании
классов,
Y2).
Здесь кванторы
связывают
только переменные
для множеств.
Поэтому, в силу
теоремы о
существовании
классов, ![]()
![]() Z
Z
![]() x
(x
x
(x ![]() Z
Z ![]()
![]() u
u![]() v
(x
=
v
(x
= ![]() & u
& u ![]() Y1
& v
Y1
& v ![]() Y2)),
а на основании
аксиомы объемности,
Y2)),
а на основании
аксиомы объемности,
![]()
![]() 1Z
1Z
![]() x
(x
x
(x ![]() Z
Z ![]()
![]() u
u![]() v
(x
=
v
(x
= ![]() & u
& u ![]() Y1
& v
Y1
& v ![]() Y2)).
Поэтому
возможно следующее
определение,
вводящее новую
функциональную
букву
Y2)).
Поэтому
возможно следующее
определение,
вводящее новую
функциональную
букву
![]() :
:
Определение.
![]() x
(x
x
(x ![]() Y1
Y1![]() Y2
Y2![]()
![]() u
u![]() v
(x
=
v
(x
= ![]() & u
& u ![]() Y1
& v
Y1
& v ![]()
![]() Y2)).
(Декартово
произведение
классов Y1 и Y2).
Y2)).
(Декартово
произведение
классов Y1 и Y2).
Определения.
X2
обозначает
X ![]() X
(в частности,
V2
обозначает
класс всех
упорядоченных
пар).
X
(в частности,
V2
обозначает
класс всех
упорядоченных
пар).
…………………………………………………………………………………………………
Xn
обозначает
Xn-1![]() X
(в частности,
Vn
обозначает
класс всех
упорядоченных
n-ок).
X
(в частности,
Vn
обозначает
класс всех
упорядоченных
n-ок).
Rel(X)
служит сокращением
для Х ![]() V2
(X есть
отношение).
V2
(X есть
отношение).
2. Пусть φ
(X,
Y)
обозначает
Х ![]() Y.
По теореме
о существовании
классов и на
основании
аксиомы объемности,
Y.
По теореме
о существовании
классов и на
основании
аксиомы объемности,
![]()
![]() 1Z
1Z![]() x
(x
x
(x ![]() Z
Z ![]() x
x ![]() Y).
Таким образом,
существует
класс Z,
элементами
которого являются
все подмножества
класса Y.
Y).
Таким образом,
существует
класс Z,
элементами
которого являются
все подмножества
класса Y.
Определение.
![]() x
(x
x
(x ![]() P
(Y)
P
(Y) ![]() x
x ![]() Y).
(P
(Y):
класс всех
подмножеств
класса Y.)
Y).
(P
(Y):
класс всех
подмножеств
класса Y.)
3. Рассмотрим
в качестве φ
(X,
Y)
формулу ![]() v
(X
v
(X ![]() v
& v
v
& v ![]() Y).
Y).
По теореме
о существовании
классов и на
основании
аксиомы объемности,
![]()
![]() 1Z
1Z![]() x
(x
x
(x ![]() Z
Z ![]()
![]() v
(x
v
(x ![]() v
& v
v
& v ![]() Y)),
т.е. существует
единственный
класс Z,
элементами
которого являются
все элементы
элементов
класса Y
и только они.
Y)),
т.е. существует
единственный
класс Z,
элементами
которого являются
все элементы
элементов
класса Y
и только они.
Определение.
![]() x
(x
x
(x ![]()
![]() (Y)
(Y) ![]()
![]() v
(x
v
(x ![]() v
& v
v
& v ![]() Y)). (
Y)). (![]() (Y):
объединение
всех элементов
класса Y)
(Y):
объединение
всех элементов
класса Y)
4. Пусть
φ (X)
есть ![]() u
(X
=
u
(X
= ![]() ).
По теореме
о существовании
классов и на
основании
аксиомы объемности,
существует
единственный
класс Z
такой, что
).
По теореме
о существовании
классов и на
основании
аксиомы объемности,
существует
единственный
класс Z
такой, что ![]() x
(x
x
(x ![]() Z
Z ![]()
![]() u
(x
=
u
(x
= ![]() )).
)).
Определение.
![]() x
(x
x
(x ![]() I
I ![]()
![]() u
(x
=
u
(x
= ![]() )).
(Отношение
тождества.)
)).
(Отношение
тождества.)
Следствие. Для всякой предикативной формулы φ (X1,…,Xn, Y1,… …, Ym)
![]()
![]() 1W(
W
1W(
W ![]() Vn &
Vn & ![]() x1…
x1…![]() xn
(
xn
(![]()
![]() W
W ![]()
![]() φ (x1,…,xn,
Y1,…,
Ym)).
φ (x1,…,xn,
Y1,…,
Ym)).
Доказательство.
В силу предложения
4, существует
класс Z,
для которого
![]() x1…
x1…![]() xn
(
xn
(![]()
![]() Z
Z ![]() φ (x1,…,xn,
Y1,…,
Ym)).
Очевидно,
искомым классом
W
является класс
W
= Z
∩ Vn;
его единственность
вытекает из
аксиомы объемности.
φ (x1,…,xn,
Y1,…,
Ym)).
Очевидно,
искомым классом
W
является класс
W
= Z
∩ Vn;
его единственность
вытекает из
аксиомы объемности.
Определение. Для всякой
предикативной
формулы φ
(X1,…,Xn,
Y1,…
…, Ym)
через ![]() φ
(x1,…,xn,
Y1,…,
Ym))
обозначается
класс всех n-ок
φ
(x1,…,xn,
Y1,…,
Ym))
обозначается
класс всех n-ок ![]() , удовлетворяющих
формуле φ
(x1,…,xn,
Y1,…,
Ym)),
т. е.
, удовлетворяющих
формуле φ
(x1,…,xn,
Y1,…,
Ym)),
т. е. ![]() u
(u
u
(u ![]()
![]()
![]() φ (x1,…,xn,
Y1,…,
Ym)
φ (x1,…,xn,
Y1,…,
Ym) ![]()
![]() x1…
x1…![]() xn(u
=
xn(u
= ![]() & φ
(x1,…,xn,
Y1,…
…, Ym))).
Следствие
оправдывает
такое определение.
В частности,
при n
= 1 получим
& φ
(x1,…,xn,
Y1,…
…, Ym))).
Следствие
оправдывает
такое определение.
В частности,
при n
= 1 получим ![]()
![]() u
(u
u
(u ![]()
![]() φ (x,
Y1,
…, Ym)
φ (x,
Y1,
…, Ym) ![]() φ (u,
Y1,…,
Ym))
(иногда
вместо
φ (u,
Y1,…,
Ym))
(иногда
вместо ![]() φ
(x1,…,xn,
Y1,…,
Ym)
применяют
запись {
φ
(x1,…,xn,
Y1,…,
Ym)
применяют
запись {![]() |
φ (x1,…,xn,
Y1,…,
Ym)}).
|
φ (x1,…,xn,
Y1,…,
Ym)}).
Примеры. 1.
Пусть φ
есть ![]()
![]() Y.
Обозначим
Y.
Обозначим ![]()
![]() (
(![]()
![]() Y)
сокращенно
через
Y)
сокращенно
через ![]() ,
тогда
,
тогда ![]()
![]()
![]() V2 &
V2 &
![]() x1
x1![]() x2(
x2(![]()
![]() Y
Y ![]()
![]()
![]() Y).
Назовем
Y).
Назовем ![]() обратным
отношением
класса Y.
обратным
отношением
класса Y.
2. Пусть
φ
есть ![]() v
(
v
(![]()
![]() Y).
Обозначим
через R(Y)
выражение
Y).
Обозначим
через R(Y)
выражение ![]() (
(![]() v
(
v
(![]()
![]() Y)).
Тогда
Y)).
Тогда ![]()
![]() u
(u
u
(u ![]() R(Y)
R(Y) ![]()
![]() v
(
v
(![]()
![]() Y)).
Класс R(Y)
называется
областью
значений
класса Y.
Очевидно,
Y)).
Класс R(Y)
называется
областью
значений
класса Y.
Очевидно, ![]() R(Y)
= D(
R(Y)
= D(![]() ).
).
Заметим, что аксиомы В1 — В7 являются частными случаями теоремы о существовании классов, т. е. предложения 4. Иными словами, вместо того, чтобы выдвигать предложение 4 в качестве схемы аксиом, можно с тем же результатом ограничиться лишь некоторым конечным числом его частных случаев. Вместе с тем, хотя предложение 4 и позволяет доказывать существование большого числа самых разнообразных классов, нам, однако, ничего еще не известно о существовании каких-либо множеств, кроме самых простых множеств таких, как 0, {0}, {0, {0}}, {{0}} и т. д. Чтобы обеспечить существование множеств более сложной структуры, введем дальнейшие аксиомы.
А к с и о м а U. (Аксиома объединения.)
![]() x
x![]() y
y![]() u
(u
u
(u ![]() y
y ![]()
![]() v
(u
v
(u ![]() v & v
v & v ![]() x)).
x)).
Эта
аксиома утверждает,
что объединение ![]() (х)
всех элементов
множества
х
является также
множеством,
т. е.
(х)
всех элементов
множества
х
является также
множеством,
т. е. ![]()
![]() x
(M(
x
(M(![]() (х))).
Множество
и
(х))).
Множество
и ![]() (х)
обозначают
также через
и
(х)
обозначают
также через
и ![]() v.
v.
Средством порождения новых множеств из уже имеющихся является образование множества всех подмножеств данного множества.
А к с и о м а W. (Аксиома множества всех подмножеств.)
![]() x
x![]() y
y![]() u
(u
u
(u ![]() y
y ![]() u
u ![]() x).
x).
Эта аксиома
утверждает,
что класс всех
подмножеств
множества х
есть также
множество; его
будем называть
множеством
всех подмножеств
множества
х. В силу
этой аксиомы,
![]()
![]() x
(M(P
(х))).
x
(M(P
(х))).
Примеры.
![]() P
(0)
= {0}.
P
(0)
= {0}.
![]() P
({0})
= {0, {0}}.
P
({0})
= {0, {0}}.
![]() P
({0,
{0}})
= {0, {0}, {0, {0}}, {{0}}}.
P
({0,
{0}})
= {0, {0}, {0, {0}}, {{0}}}.
Значительно более общим средством построения новых множеств является следующая аксиома выделения.
А к с и о м а S.
![]() x
x![]() Y
Y ![]() z
z![]() u
(u
u
(u ![]() z
z ![]() u
u ![]() x & u
x & u ![]() Y).
Y).
Таким образом,
для любого
множества х
и для любого
класса Y
существует
множество,
состоящее
из элементов,
общих для х
и Y.
Следовательно,
![]()
![]() x
x![]() Y
(M
(x
∩ Y)),
т. е. пересечение
множества с
классом есть
множество.
Y
(M
(x
∩ Y)),
т. е. пересечение
множества с
классом есть
множество.
Предложение 5. ![]()
![]() x
x![]() Y
(Y
Y
(Y ![]() x
x ![]() M
(Y)) (т. е. подкласс
множества
есть множество).
M
(Y)) (т. е. подкласс
множества
есть множество).
Доказательство.
![]()
![]() x
(Y
x
(Y ![]() x
x ![]() Y
∩ x
= Y)
и
Y
∩ x
= Y)
и
![]()
![]() x
(M
(Y
∩ x)).
x
(M
(Y
∩ x)).
Так как всякая предикативная формула A(у) порождает соответствующий класс (предложение 4), то из аксиомы S следует, что для любого множества х класс всех его элементов, удовлетворяющих данной предикативной формуле A(у), есть множество.
Однако для полного развития теории множеств потребуется аксиома, более сильная, чем аксиома S. Введем предварительно несколько определений.
Определения
Un
(X)
означает
![]() x
x![]() y
y![]() z
(
z
(![]()
![]() X
&
X
& ![]()
![]() X
X ![]() y
= z).
y
= z).
(X однозначен.)
Fnc
(X)
означает X ![]() V2
& Un
(X). (X есть
функция.)
V2
& Un
(X). (X есть
функция.)
Y
1
X
означает
X
∩ (Y ![]() V).
(Ограничение
Х областью
Y.)
V).
(Ограничение
Х областью
Y.)
Un1
(X)
означает
Un
(X)
& Un
(![]() ). (X
взаимно
однозначен.)
). (X
взаимно
однозначен.)
X‘Y 
Если существует
единственное
z
такое, что ![]()
![]() X,
то z
= X‘y;
в противном
случае X‘y
= 0. Если Х
есть функция,
а у —
множество из
области определения
X, то X‘y
есть значение
этой функции,
примененной
к у (В
дальнейшем
будем по мере
необходимости
вводить новые
функциональные
буквы и предметные
константы, как
только будет
ясно, что соответствующее
определение
может быть
обосновано
теоремой о
единственности.
В настоящем
случае происходит
введение некоторой
новой функциональной
буквы h
с сокращенным
обозначением
Х‘Y
вместо h
(X, Y)).
X,
то z
= X‘y;
в противном
случае X‘y
= 0. Если Х
есть функция,
а у —
множество из
области определения
X, то X‘y
есть значение
этой функции,
примененной
к у (В
дальнейшем
будем по мере
необходимости
вводить новые
функциональные
буквы и предметные
константы, как
только будет
ясно, что соответствующее
определение
может быть
обосновано
теоремой о
единственности.
В настоящем
случае происходит
введение некоторой
новой функциональной
буквы h
с сокращенным
обозначением
Х‘Y
вместо h
(X, Y)).
X‘‘Y = R(Y 1 X). (Если Х есть функция, то X‘‘Y есть область значений класса X, ограниченного областью Y.)
А к с и о м а R. (Аксиома замещения.)
![]() x
(Un (X)
x
(Un (X) ![]()
![]() y
y![]() u
(u
u
(u ![]() y
y ![]()
![]() v
(
v
(![]()
![]() X & v
X & v ![]() X))).
X))).
Аксиома замещения утверждает, что если класс Х однозначен, то класс вторых компонент тех пар из X, первые компоненты которых принадлежать, является множеством (эквивалентное утверждение: M(R (x 1X))) Из этой аксиомы следует, что если Х есть функция, то область значений результата ограничения Х посредством всякой области, являющейся множеством, также есть множество.
Следующая аксиома обеспечивает существование бесконечных множеств.
А к с и о м а I. (Аксиома бесконечности.)
![]() x
(0
x
(0
![]() x &
x & ![]() u
(u
u
(u ![]() x
x ![]() u
u ![]() {u}
{u}
![]() x)).
x)).
Аксиома
бесконечности
утверждает,
что существует
такое множество
х, что
0 ![]() x,
и если и
x,
и если и ![]() x,
то и
x,
то и ![]() {и}
также принадлежит
х. Для
такого множества
х, очевидно,
{0}
{и}
также принадлежит
х. Для
такого множества
х, очевидно,
{0} ![]() x,
{0, {0}}
x,
{0, {0}} ![]() x,
{0, {0}, {0, {0}}}
x,
{0, {0}, {0, {0}}} ![]() x и т. д. Если
теперь положим
1 = {0}, 2 = {0, 1}, … , n
= {0, 1, … , n
– 1}, то для любого
целого п
≥ 0 будет
выполнено п
x и т. д. Если
теперь положим
1 = {0}, 2 = {0, 1}, … , n
= {0, 1, … , n
– 1}, то для любого
целого п
≥ 0 будет
выполнено п ![]() х, и при
этом 0 ≠ 1, 0 ≠ 2, 1 ≠ 2, 0 ≠ 3,
1 ≠ ≠ 3, 2 ≠ 3, …
х, и при
этом 0 ≠ 1, 0 ≠ 2, 1 ≠ 2, 0 ≠ 3,
1 ≠ ≠ 3, 2 ≠ 3, …
Список аксиом теории NBG завершен. Видно, что NBG имеет лишь конечное число аксиом, а именно: аксиому Т (объемности), аксиому Р (пары), аксиому N (пустого множества), аксиому S (выделения), аксиому U (объединения), аксиому W (множества всех подмножеств), аксиому R (замещения), аксиому I (бесконечности) и семь аксиом существования классов В1—В7.
Убедимся
теперь в том,
что парадокс
Рассела невыводим
в NBG.
Пусть Y
= ![]() (x
(x ![]() x)
,т. е.
x)
,т. е. ![]() х
(х
х
(х ![]() Y
Y ![]() х
х ![]() х). (Такой
класс Y
существует,
в силу теоремы
о существовании
классов (предложение
4), так как формула х
х). (Такой
класс Y
существует,
в силу теоремы
о существовании
классов (предложение
4), так как формула х ![]() х предикативна.)
В первоначальной,
т. е. не сокращенной,
символике эта
последняя
формула записывается
так:
х предикативна.)
В первоначальной,
т. е. не сокращенной,
символике эта
последняя
формула записывается
так: ![]() X
(M(X)
X
(M(X) ![]() (X
(X ![]() Y
Y ![]() X
X
![]() X)).
Допустим
M(Y).
Тогда Y
X)).
Допустим
M(Y).
Тогда Y ![]() Y
Y ![]() Y
Y
![]() Y,
что, в силу
тавтологии
(A
Y,
что, в силу
тавтологии
(A ![]()
![]() A)
A) ![]() A
& &
A
& & ![]() A,
влечет Y
A,
влечет Y ![]() Y
Y ![]() Y
Y
![]() Y.
Отсюда по теореме
дедукции получаем
Y.
Отсюда по теореме
дедукции получаем ![]() M(Y)
M(Y)![]() (Y
(Y ![]() Y
Y ![]() Y
Y
![]() Y),
а затем, в силу
тавтологии
(B
Y),
а затем, в силу
тавтологии
(B ![]() (A
&
(A
& ![]() A))
A))![]()
![]() B
, получаем
и
B
, получаем
и ![]() М(Y).
Таким образом,
рассуждения,
с помощью которых
обычно выводится
парадокс Рассела,
в теории NBG
приводят всего
лишь к тому
результату,
что Y
есть собственный
класс, т. е. не
множество.
Здесь имеем
дело с типичным
для теории NBG
способом избавления
от обычных
парадоксов
(например, парадоксов
Кантора и
Бурали-Форти).
М(Y).
Таким образом,
рассуждения,
с помощью которых
обычно выводится
парадокс Рассела,
в теории NBG
приводят всего
лишь к тому
результату,
что Y
есть собственный
класс, т. е. не
множество.
Здесь имеем
дело с типичным
для теории NBG
способом избавления
от обычных
парадоксов
(например, парадоксов
Кантора и
Бурали-Форти).
Определения
X
Irr
Y
означает ![]() y
(y
y
(y ![]() Y
Y ![]()
![]()
![]() X)
& Rel
(X).
X)
& Rel
(X).
(X есть иррефлексивное отношение на Y.)
X
Tr
Y
означает
Rel
(X)
& ![]() u
u![]() v
v![]() w
(u
w
(u![]() Y
& v
Y
& v![]() Y
& w
Y
& w![]() Y
&
Y
&
& ![]()
![]() X
&
X
&![]()
![]() X
& X
X
& X ![]()
![]()
![]() X).
X).
(X есть транзитивное отношение на Y.)
X Part Y означает (X Irr Y) & (X Tr Y).
(X частично упорядочивает Y.)
X
Con
Y
означает
Rel(X)
& ![]() u
u![]() v
(u
v
(u![]() Y
& v
Y
& v![]() Y
& u
≠ v
Y
& u
≠ v ![]()
![]()
![]()
![]() X
X ![]()
![]()
![]() X).
X).
X Tot Y означает (X Irr Y) & (X Tr Y) & (X Con Y).
(X упорядочивает Y.)
X
We
Y
служит
обозначением
для Rel(X)
& (X
Irr
Y)
& ![]() Z
(Z
Z
(Z![]() Y
&
Y
&
& Z
≠ 0 ![]()
![]() y
(y
y
(y ![]() Z
&
Z
& ![]() v
(v
v
(v ![]() Z
& v
≠ y
Z
& v
≠ y ![]()
![]()
![]() X &
X &
& ![]()
![]() X))).
X))).
(X вполне упорядочивает Y, т. е. отношение Х иррефлексивно на Y, и всякий непустой подкласс класса Y имеет наименьший в смысле отношения Х элемент.)
§2. Аксиома выбора. Лемма Цорна.
Аксиома выбора является одним из самых знаменитых и наиболее оспариваемых утверждений теории множеств.
Следующие формулы эквивалентны:
А к с и о м а в ы б о р а (АС): Для
любого множества
х существует
функция f такая, что для
всякого непустого
подмножества
у множества
х f‘
y ![]() y
(такая функция
называется
в ы б и р а ю щ е
й ф у н к ц и е й
для х).
y
(такая функция
называется
в ы б и р а ю щ е
й ф у н к ц и е й
для х).
М у л ь т и п л и к а т и в н а я а к с и о м а (Mult): Для любого множества х непустых и попарно непересекающихся множеств, существует множество у (называемое в ы б и р а ю щ и м м н о ж е с т в о м для х), которое содержит в точности по одному элементу из каждого множества, являющегося элементом х.
![]() u
(u
u
(u ![]() x
x ![]() u ≠ 0 &
u ≠ 0 & ![]() v
(v
v
(v ![]() x & v ≠ u
x & v ≠ u ![]() v
∩ u = 0))
v
∩ u = 0))![]()
![]()
![]() y
y![]() u
(u
u
(u ![]() x
x ![]()
![]() 1w
(w
1w
(w ![]() u ∩ y)).
u ∩ y)).
П р и н ц и п в п о л н е у п о
р я д о ч е н и я
(W.
O.):
Всякое
множество
может быть
вполне упорядочено. ![]() x
x ![]() y
(y We x).
y
(y We x).
Т р и х о т о
м и я (Trich): ![]() x
x![]() y
(x
y
(x
![]() y
y![]() y
y ![]() x).
x).
Л е м м а Ц о р н а (Zorn): Если в частично упорядоченном множестве х всякая цепь (т. е. всякое упорядоченное подмножество) имеет верхнюю грань, то в х существует максимальный элемент.
![]() x
x![]() y
((y Part x) &
y
((y Part x) & ![]() u
(u
u
(u ![]() x & y Tot u
x & y Tot u ![]()
![]() v
(v
v
(v ![]() x &
x &![]() w
(w
w
(w ![]() u
u ![]() w
=
w
=
= v ![]()
![]()
![]() y)))
y))) ![]()
![]() v
(v
v
(v ![]() x
&
x
&![]() w
(w
w
(w ![]() x
x ![]()
![]()
![]() y))).
y))).
Доказательство.
1. ![]() (W.
O.)
(W.
O.) ![]() Trich.
Пусть даны
множества х
и у.
Согласно (W.
O.),
х и у
могут быть
вполне упорядочены.
Поэтому существуют
такие порядковые
числа α и β, что
х
Trich.
Пусть даны
множества х
и у.
Согласно (W.
O.),
х и у
могут быть
вполне упорядочены.
Поэтому существуют
такие порядковые
числа α и β, что
х ![]() α и y
α и y
![]() β. Но так
как α
β. Но так
как α ![]() β или β
β или β ![]() α, то либо
x
α, то либо
x
![]() y,
либо y
y,
либо y ![]() x.
x.
2. ![]() Trich
Trich ![]() (W.
O.).
Пусть дано
множество х.
Согласно теореме
Хартогса, существует
такое порядковое
число α, которое
не равномощно
никакому подмножеству
множества х.
Тогда, в силу
Trich,
х равномощно
некоторому
подмножеству
у порядкового
числа α, и вполне
упорядочение
Еу
множества у
порождает
некоторое
вполне упорядочение
множества х.
(W.
O.).
Пусть дано
множество х.
Согласно теореме
Хартогса, существует
такое порядковое
число α, которое
не равномощно
никакому подмножеству
множества х.
Тогда, в силу
Trich,
х равномощно
некоторому
подмножеству
у порядкового
числа α, и вполне
упорядочение
Еу
множества у
порождает
некоторое
вполне упорядочение
множества х.
3. ![]() (W.
O.)
(W.
O.) ![]() Mult.
Пусть х
есть некоторое
множество
непустых, попарно
непересекающихся
множеств. Согласно
(W.
O.),
существует
отношение R,
вполне упорядочивающее
множество
Mult.
Пусть х
есть некоторое
множество
непустых, попарно
непересекающихся
множеств. Согласно
(W.
O.),
существует
отношение R,
вполне упорядочивающее
множество ![]() (х).
Следовательно,
существует
такая определенная
на х
функция f,
что f‘u
для любого
и
(х).
Следовательно,
существует
такая определенная
на х
функция f,
что f‘u
для любого
и ![]() х есть
наименьший
относительно
R
элемент и.
(Заметим, что
и
х есть
наименьший
относительно
R
элемент и.
(Заметим, что
и ![]()
![]() (х).)
(х).)
4. ![]() Mult
Mult ![]() AC.
Для любого
множества х
существует
функция g
такая, что
если и
есть непустое
подмножество
х, то
g‘и
= u
AC.
Для любого
множества х
существует
функция g
такая, что
если и
есть непустое
подмножество
х, то
g‘и
= u ![]() {и}.
Пусть х1
—область
значении функции
g.
Легко видеть,
что х1
является
множеством
непустых попарно
непересекающихся
множеств. На
основании
Mult,
для х1
существует
выбирающее
множество у.
Отсюда, если
0 ≠ u
и u
{и}.
Пусть х1
—область
значении функции
g.
Легко видеть,
что х1
является
множеством
непустых попарно
непересекающихся
множеств. На
основании
Mult,
для х1
существует
выбирающее
множество у.
Отсюда, если
0 ≠ u
и u ![]() х, то и
х, то и ![]() {и}
{и} ![]() х1 и у
содержит и
притом единственный
элемент
х1 и у
содержит и
притом единственный
элемент![]() из и
из и ![]() {и}.
Функция f‘
u
= v
является
искомой выбирающей
функцией для
х.
{и}.
Функция f‘
u
= v
является
искомой выбирающей
функцией для
х.
5. ![]() АС
АС ![]() Zorn.
Пусть у
частично
упорядочивает
непустое множество
х таким
образом, что
всякая y-цепь
в х имеет
в х
верхнюю грань.
На основании
АС, для х
существует
выбирающая
функция f.
Рассмотрим
произвольный
элемент b
множества х,
и по
трансфинитной
индукции определим
функцию F
такую, чтобы
выполнялось
F‘0
= b
и F‘α
= f‘u
для любого α,
где u
есть множество
всех таких
верхних граней
v
множества F‘‘
α относительно
упорядочения
у, что
v
Zorn.
Пусть у
частично
упорядочивает
непустое множество
х таким
образом, что
всякая y-цепь
в х имеет
в х
верхнюю грань.
На основании
АС, для х
существует
выбирающая
функция f.
Рассмотрим
произвольный
элемент b
множества х,
и по
трансфинитной
индукции определим
функцию F
такую, чтобы
выполнялось
F‘0
= b
и F‘α
= f‘u
для любого α,
где u
есть множество
всех таких
верхних граней
v
множества F‘‘
α относительно
упорядочения
у, что
v ![]() х и v
х и v ![]() F‘‘
α. Пусть
β есть наименьшее
порядковое
число, которому
соответствует
пустое множество
верхних граней
v
множества
F‘‘
β относительно
упорядочения
v,
принадлежащих
x
и не принадлежащих
F‘‘
β. (Порядковые
числа, обладающие
таким свойством,
существуют;
в противном
случае функция
F
была бы взаимно
однозначной
с областью
определения
Оп и
с некоторым
подмножеством
множества
х в
качестве области
значений, откуда
по аксиоме
замещения R
следовало бы,
что Оп
есть множество.)
Пусть g
= β
1 F.
Функция g
взаимно однозначна
и что если α
F‘‘
α. Пусть
β есть наименьшее
порядковое
число, которому
соответствует
пустое множество
верхних граней
v
множества
F‘‘
β относительно
упорядочения
v,
принадлежащих
x
и не принадлежащих
F‘‘
β. (Порядковые
числа, обладающие
таким свойством,
существуют;
в противном
случае функция
F
была бы взаимно
однозначной
с областью
определения
Оп и
с некоторым
подмножеством
множества
х в
качестве области
значений, откуда
по аксиоме
замещения R
следовало бы,
что Оп
есть множество.)
Пусть g
= β
1 F.
Функция g
взаимно однозначна
и что если α
Похожие работы
... действительных чисел. 3.3. Конечные и бесконечные множества Конечное множество - множество, состоящее из конечного числа элементов. Пример. A = {1, 2, 3, 4, 5}. Основной характеристикой конечного множества является число его элементов. Теория конечных множеств изучает правила: как, зная количество элементов некоторых множеств, вычислить количество элементов других множеств, которые составлены из ...
... нашем примере: сила, с которой брошена монета, форма монеты и многие другие). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны. Поэтому теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет, она просто не в силах это сделать. Еще пример, выпадение снега в Москве 30 ноября является ...
... понятия вероятности задача некоторой несостоятельности классического определения вероятности была решена. Однако наблюдаются попытки дать трактовку вероятности с более широких позиций, в том числе и с позиций теории информации. 2. Динамика развития понятия математического ожидания 2.1 Предпосылки введения понятия математического ожидания Одним из первых приблизился к определению понятия ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...

0 комментариев