Эффективные методы одномерного поиска (метод Золотого сечения и метод Фибоначчи);

1.  Эффективные методы одномерного поиска (метод Золотого сечения и метод Фибоначчи);

2.  Методы полиномиальной интерполяции (Пауэлл, Ньютон, сплайн-интерполяция).

Для конкретизации модельной схемы помимо процедуры вычисления длины шага h_k необходимо также задавать алгоритм расчета требуемого направления поиска .

В отличие от одномерного случая, где возможно всего лишь два направления движения ( вперед и назад), уже в двумерной задаче множество направлений поиска является бесконечным.

В этом случае возникает проблема выбора направления поиска . Именно способ вычисления  и определяет «лицо» алгоритма безусловной минимизации. Поэтому названия алгоритмам оптимизации даются по реализованным в них процедурам вычисления .

В данной курсовой работе в качестве метода синтеза применяется метод сопряженных градиентов. В группе данных методов процедура вычисления направления поиска не предполагает решения каких либо СЛАУ. Эти методы принципиально отличаются от методов Ньютна и квазиньютоновских методов.

Рассмотрим задачу поиска минимума квадратичной функции вида:

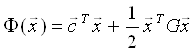
с,G - вектор и полноопределенная матрица, независящие от вектора  .

Предполагается, что нам известно к-тое приближение в точке минимума и (к+1) линейно независимых векторов .

Будем искать точку минимума целевой функции Ф() на линейном множестве векторов +Р_к, где Р_к – (к+1)-мерное множество, образованное линейно независимыми векторами.

Множества, образованные вида +Р_к называются линейными многообразиями.

Задача сводится к нахождению точки минимума Ф() на этом линейном многообразии.

Для решения этой задачи сначала вводится матрица Р_к=[]. Введение такой матрицы позволяет сформулировать задачу поиска минимума функции Ф() на многообразии +Р_к следующим образом: найти

То есть надо найти вектор , таким образом, чтобы точка  была бы точкой минимума функции .

Для решения этой задачи необходимо сначала в функцию Ф(х) вместо  , затем продифференцировать получившуюся функцию по вектору , приравнять результат к нулю и оттуда выразить вектор, который является решением задачи.

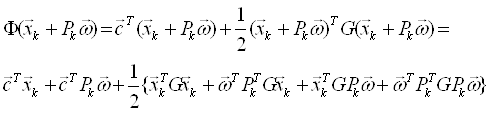
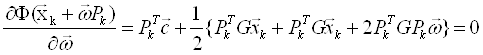
Если есть функция

, то

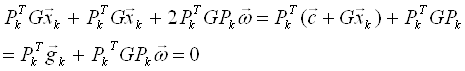
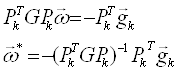
Тогда точка минимума

 (1)

Формулу (1) можно рассматривать как формулу рекуррентного расчета точки в классических методах спуска. Другими словами, формула (1) описывает процедуру пошаговой минимизации квадратичной функции Ф(х).

Формула (1) обладает рядом свойств:

 ,

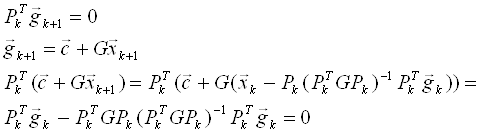
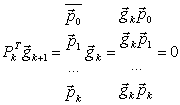то есть каждая компонента должна быть равна нулю

Так как предполагается, что все точки x_j при j=1,к рассчитывается по формуле (1), то справедливо следующее свойство:

 i>j

Тогда формулу (1) можно преобразовать

е_к – (к+1) столбец единичной матрицы

С учетом всего этого формула (1) примет вид

Последнее выражение можно упростить, если матрица  будет ортогональной. Ето возможно сделать, если вектора  выбирать специальным образом. Вектора  должны быть сопряженными относительно матрицы G, то есть должны выполняться следующие соотношения

Тогда получаем упрощенное выражение

Таким образом мы установили, что среди методов минимизации квадратичных функций, укладывающихся в общую модельную схему, существует метод, к-тая итерация которого приводит в точку минимума функции Ф() на многообразии +Р_к-1.

Теоретически такой метод конечен, то есть он обеспечивает нахождение минимума функции Ф() не более чем за N шагов (N-размерность задачи), так как многообразие +Р_к-1 на последнем N-том шаге совпадает с множеством значений аргумента  и следовательно, если минимум функции Ф() не был найден ранее, то он обязательно будет найден на этом шаге.

Для того, чтобы полностью определить метод сопряженных градиентов необходимо определить правило выбора вектора . Это правило выглядит следующим образом:

 (2)

 - скаляр, который выбирается по двум теоретически эквивалентным формулам:

1.  - формула Флетчера-Ривса

2. 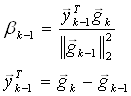 - формула Полака-Рибьера

Метод сопряженных градиентов для квадратических функций легко обобщается на случай целевой функции общего вида. Для этого необходимо ввести процедуру одномерного поиска длины шага h_k и определиться, всегда ли направление поиска будет выдаваться по формуле (2) или допустимы отступления от нее. Такие отступления называются восстановлениями или рестартами. В начале рестарта вектор . Метод сопряженных градиентов, использующий такие рестарты, называется традиционным. Традиционный метод сопряженных градиентов сходится в тех же предположениях, что и метод наискорейшего спуска. Он обладает теоретической N-шаговой сверхлинейной сходимостью, но из-за наличия ошибок округления реальная скорость сходимости метода сопряженных градиентов практически всегда линейна.

Таким образом, хотя схема метода сопряженных градиентов далека от идеала, тем не менее этот метод остается единственным разумным средством для решения задачи оптимизации очень большой размерности (число переменных более 1000000).