Навигация
Погрешности произведения и частного приближенных чисел
5. Погрешности произведения и частного приближенных чисел
Формулы для оценки абсолютной погрешности произведения и частного является более сложными, чем для суммы и разности. Поэтому для частного и произведения абсолютные погрешности обычно определяют, используя известную формулу
![]() ,
,
для a = x1x2...xn или a = x1/x2, где относительная погрешность произведения приближенных чисел определяется следующим образом:
![]()
Формула показывает, что относительные погрешности нескольких приближенных чисел складываются при выполнении операции умножения над этими числами.
Для предельной относительной погрешности формула имеет вид:
![]()
Аналогичным образом можно получить оценки погрешности частного двух приближенных чисел:
 ;
; 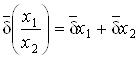
6. Погрешность функции
Основная задача теории погрешностей заключается в следующем: по известным значениям погрешностей исходных данных определить погрешность некоторой функции от этих величин.
Пусть задана функция f(x), значение которой требуется вычислить для приближенного значения аргумента ![]() , имеющего известную предельную абсолютную погрешность
, имеющего известную предельную абсолютную погрешность ![]() . Если функция f(x) дифференцируема в точке x0, то погрешность ее значения в этой точке можно оценить как
. Если функция f(x) дифференцируема в точке x0, то погрешность ее значения в этой точке можно оценить как
погрешность вычислительный приближенный функция
![]() .
.
Считается, что формула справедлива, если относительные ошибки аргумента и результата малы по сравнению с единицей, т.е.
dx0 << 1 и df(x0) << 1.
Нетрудно заметить, что вычисление функции в точке с большим модулем производной может привести к значительному увеличению погрешности результата по сравнению с погрешностью аргумента (катастрофическая потеря точности).
7. Погрешность функции нескольких переменных
Пусть y = f(x1, x2, …, xn) – приближенное значение функции от приближенных аргументов![]() ,
, ![]() , …,
, …, ![]() , которые имеют абсолютные ошибки
, которые имеют абсолютные ошибки ![]() ,
, ![]() , …,
, …, ![]() .
.
Для определения ![]() используют принцип наложения ошибок, согласно которому учитывают влияние погрешностей каждого из аргументов в отдельности, а затем полученные погрешности суммируют. Для этого вначале временно предполагают, что все аргументы, кроме x1 являются точными числами, и находится соответствующая частная ошибка, вносимая только погрешностью этого аргумента
используют принцип наложения ошибок, согласно которому учитывают влияние погрешностей каждого из аргументов в отдельности, а затем полученные погрешности суммируют. Для этого вначале временно предполагают, что все аргументы, кроме x1 являются точными числами, и находится соответствующая частная ошибка, вносимая только погрешностью этого аргумента ![]() :
:
![]() ,
,
где производная определяется по x1. Затем вычисляется частная ошибка, вносимая аргументом ![]() :
:
![]() .
.
В итоге искомая погрешность функции ![]() , определяется суммой всех частных ошибок:
, определяется суммой всех частных ошибок:
![]() .
.
Условиями применимости этой формулы считается выполнение следующих неравенств:
dxi << 1 (i = ![]() ); d f(x1, x2, …, xn) << 1.
); d f(x1, x2, …, xn) << 1.
8. Обратная задача теории погрешностей
Обратная задача теории погрешностей заключается в определении погрешностей исходных данных по заданной погрешности результата. С использованием понятия функции нескольких переменных эта задача формулируются следующим образом: определить предельные погрешности аргументов функции, чтобы погрешность функции в целом не превышала бы заданной величины.
Эта задача является математически неопределенной, так как одна и та же погрешность результата может быть получена при разных погрешностях исходных данных. В простейшем случае для решения этой задачи используют принцип равных влияний, согласно которому в формуле для определения предельной абсолютной погрешности функции нескольких аргументов вида
![]() .
.
все слагаемые из правой части принимаются равными:
![]()
Отсюда значения предельных абсолютных погрешностей аргументов определяются следующим образом:
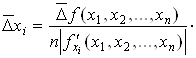
Список литературы
1. Адаптивные телеизмерительные системы, под ред. А. Б. Фремке, М. 1981 г.
2. Левин, Плоткин, Цифровые системы передачи информации, 1982 г.
3. Свиридов Н. Г. Проектирование РТС передачи информации Рязань, РРТИ, 1988 г.
Похожие работы
... нельзя рассматривать как единое целое. Кроме того, необходимо кроме сумматора иметь и вычитатель. В результате этого прямой код не применяется для выполнения операции алгебраического сложения, но применяется для выполнения операций умножения и деления. 1.1.3 Дополнительный код В дополнительном коде операция вычитания заменяется операцией алгебраического сложения. При этом знаковый разряд и ...
... находится в соответствии с данной выше оценкой погрешности и, кроме того, свидетельствует, что формула Симпсона значительно точнее формулы трапеций. Поэтому формулу Симпсона для приближенного вычисления определенных интегралов используют чаще, чем формулу трапеций. Как отмечалось выше, приближенные формулы для вычисления определенного интеграла применяют в тех случаях, когда первообразная ...
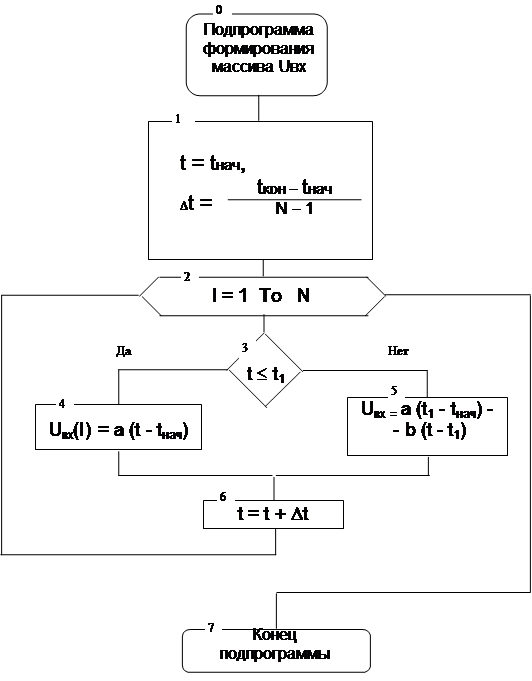
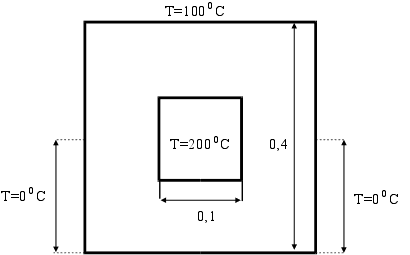
... В данной работе решаются задачи машинного анализа электрических цепей. В курсовом проекте необходимо для заданной электрической цепи по известному входному сигналу UВХ(t) построить выходной сигнал UВЫХ(t) , а затем определить некоторые его характеристики W. Характеристика W вычисляется с погрешностью не более 0.1. Погрешность вычисления величины W зависит от количества расчетных точек N, для ...
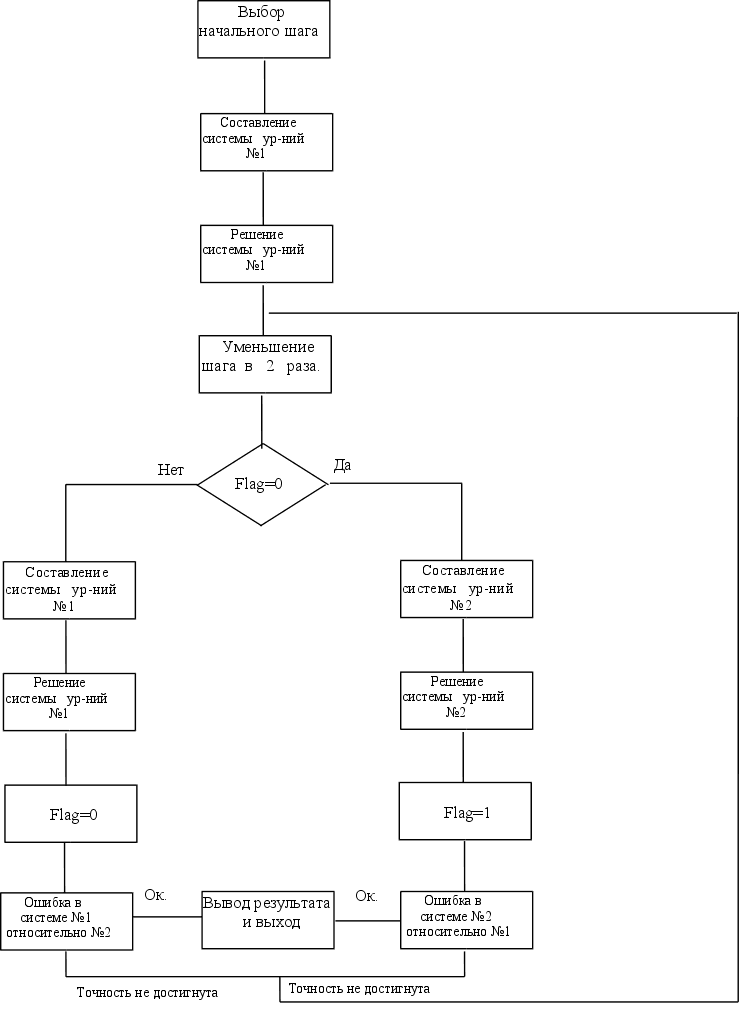
... получают последовательные приближения до тех пор, пока действительная погрешность корней не станет меньше заданной. Различные методы отличаются друг от друга способом вычисления очередного приближения, но во всех методах существуют две главные проблемы: обеспечение сходимости процесса итераций; оценка достигнутой погрешности. Пусть дана линейная система ...

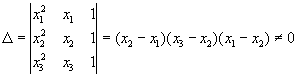
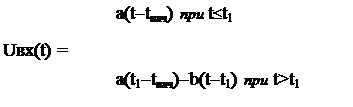
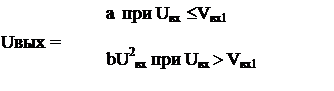


0 комментариев