Метод Шенкса

2. Метод Шенкса

Прямий метод розрахунку дискретного логарифма може використати два варіанти: - кратне додавання точки  до збігу із точкою  (шлях від точки  до точки ) або шлях від точки  до точки. У найгіршому випадку для визначення числа  із точки  може знадобитися до  додавань точки ( при  маємо множину зворотних за знаком точок, - координати яких уже відомі). Обчислювальна складність безпосереднього розрахунку дискретного логарифма оцінюється числом операцій . Щоб скоротити шлях до збігу (колізії) з відомою точкою, природно на всьому шляху поставити маркери , , координати яких визначено на етапі попередніх обчислень. Рухаючись від точки  до найближчого маркера, ми істотно скорочуємо зону пошуку (рис 1). Виникає лише питання, як розставити маркери?

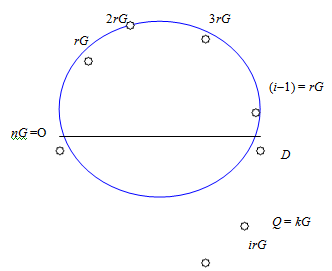
Рисунок 1 - Подання елементів циклічної групи точками на колі й інтервал аналізу за методом Шенкса

По суті введення маркерів - це обмін обчислень на пам'ять. Якщо об'єми цих ресурсів зробити рівними, то відстань між маркерами слід вибирати рівною  . Ця ідея запропонована Д.Шенксом.

Метод Шенкса часто називають методом великих і малих кроків (Giant step-Baby step). Маркери  - це Giant step. Номери  цих точок з їх -координатами зберігаються в пам'яті. Baby step – це послідовні додавання точок  після чого обчислені -координати порівняюються з координатами маркерів. При збігу координат отримуємо , звідки визначається шукане значення . Метод Шенкса є детерміністським.

Обчислювальна складність методу  оцінюється як середнє число малих кроків. Основний недолік методу – надмірний об'єм необхідної пам'яті, пропорційний .

Крім того, на кожному кроці порівняння координат здійснюється по всіх точках, що зберігаються в пам'яті. Для задач реального криптоаналізу метод не знайшов застосування. Однак, часто метод Шенкса приводиться як теоретична основа для інших, більш практичних методів рішення .

3.  Метод ділення точок на два ( продовження)

Він заснований на використанні точок <P> з максимальним порядком ,  (коефіцієнт кривої a=0). Задамо рекурентну функцію ділення-відрахування

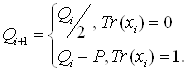
 (1)

Оскільки кожне ділення дає дві точки, повна процедура утворює дерево розв’язків із  галузями ( - число віднімань точки ). В ідеальному випадку, при правильному виборі точок ділення, одна з галузей найбільш коротким шляхом веде до точки , а інша – . При цьому двійковий запис алгоритму ділення (0) або відрахування – ділення (1) дає шукане число  або . Для цього буде потрібно не більше  ділень. Зрозуміло, при випадковому виборі точок ділення ймовірність знаходження таких галузей мізерно мала.

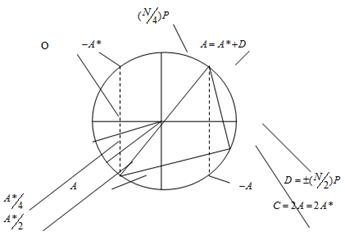
Точки групи <P> зручно подати у вигляді еквідистантних точок кола, починаючи відлік від точки ПРО, розташованої ліворуч за годинниковою стрілкою (рис. 2). Будь-якій парній точці групи <P> ®  відповідають дві точки ділення  й , розташовані на одній діагоналі кола й пов'язані співвідношенням  із точкою  другого порядку. Значення точок ,  верхнього півкола можна розглядати як додатні, а нижнього півкола  - як від’ємні. Координати  кожної такої пари збігаються, а . У процедурі ділення, що прагне до точки , можна ігнорувати знак точки, зазначимо, що є лише - координата точки. Назвемо "правильною" точкою ділення точку лівого півкола (на рис 2 – точка ). Послідовний вибір "правильних" точок ділення в процедурі  веде до точки  й, відповідно до розв’язання . Злом криптосистеми, у такий спосіб зводиться до вирішення еквівалентних проблем:

– визначення, у якому пів кола групи <P> перебуває деяка точка цієї групи;

– визначення співвідношення (більше - менше) між двома довільними
точками  й  групи <P>;

– визначення парності ( непарності) числа  для точки ;

– чи виконується редукція за модулем  при подвоєнні довільної точки  із групи  порядку ?

Доки відповісти на ці запитання не вдається ECC залишається стійкою криптосистемою з експоненційною складністю розв’язання . Для криптоаналізу зовсім необов'язково прийти до точки  або , достатньо знайти точку з -координатою точки, що раніше зустрічалася в цій процедурі, або будь-якої іншої відомої точки групи <P>. У першому випадку рішення  при колізії  близько до - методу Полларда, у другому – до методу Шенкса.

Доцільно використовувати максимально можливу кількість інформації (передрозрахунки) з метою збільшення ймовірності колізій, однак це веде до збільшення кількості перевірок і розширення пам'яті.

крива поле дискретний логарифмування атака

Рисунок 2 - Геометрична ілюстрація методу ділення точок кривої на два Якщо в 1 залишити лише одну операцію ділення на два з вибором точки із групи , то ітераційна процедура ділення на два в остаточному підсумку також призведе до точки  (або іншої відомої точки), якщо 2 є примітивним елементом поля . Послідовне ділення точок на два вимагає в НБ лише одне множення в полі на кожному кроці, інші операції практично не вимагають витрат. При цьому, імовірно, можна досягти максимальної швидкості криптоаналізу. Цей метод, однак, рівносильний повному перебору всіх точок. Більш доцільним, можливо, є випадковий пошук колізій зі складністю . 4. Аномальні криві й криві над розширеннями малого поля

Аномальні криві над розширеннями поля  (криві Коблиця) виду ,  мають особливості структури групи E, що дозволяють зменшити в  раз об'єм аналізованих точок кривої (у порівнянні із групою загальної структури) і, відповідно, у  раз обчислювальну складність пошуку колізій. Це пов'язано з виникненням класів еквівалентності точок кривої, породжуваних послідовним піднесенням у квадрат координат вихідної точки.

Позначимо функцію  при цьому  Для будь-якої точки  порядку  кривої  над полем  визначається ендоморфізм Фробеніуса (відображення поля в поле), який задовольняє характеристичне рівняння

Тут операція додавання визначена як додавання в групі E, а параметр  називають слідом ендоморфізма Фробеніуса. Зокрема, для кривої Коблиця з коефіцієнтами з поля  й параметром  маємо

Тому що функція  не змінює порядку точки, справедлива рівність , при цьому , а характеристичне рівняння Фробеніуса приймає вигляд

Розв’язання цього квадратного рівняння в кільці  дає значення параметра , що визначає всі точки класу еквівалентності

Через те, що їхні координати визначаються послідовним піднесенням у квадрат, простіше всього їх виразити в НБ, у якому їх -бітовий запис утворює циклічний код із  слів для кожної координати. Такі точки називають помітними. Задача розв’язання , таким чином, зводиться до пошуку класу еквівалентності з точністю до циклічного зсуву, що практично не вимагає додаткових обчислень. Неважко переконатися, що для підгрупи  точок цієї кривої порядку  коренем рівняння

є значення , а класи еквівалентності містять точки

Для точок максимального порядку  корінь рівняння

дорівнює  Один із класів еквівалентності точок даного порядку включає точки . Їхні координати утворюються послідовним піднесенням у квадрат. Усього є 4 класи еквівалентності точок максимального порядку.

В порівнянні із загальним типом груп  аномальні бінарні криві поступаються у стійкості в  раз, що не є катастрофічною втратою. Для полів з розширенням  втрата складає не більше 4-х біт. Тому з урахуванням високої технологічності такі криві не виключаються із криптографічних застосувань і входять у відомі стандарти. Подібні ж міркування справедливі, якщо як вихідну прийняти криву ,  над малим полем , після чого ту ж криву розглядати над розширенням  (при цьому як і раніше ). Слід Фробеніуса  визначає порядок кривої над підполем  (і розв’язання характеристичного рівняння для скаляра ), а слід  - порядок кривої над полем . Виникнення класів еквівалентності точок кривої над таким розширенням приводить до втрати складності криптоатаки в  раз. Крім того, поле  є композиційним і містить принаймні підполя . Такі криві уразливі стосовно атаки методом спуску Вейля.

Аномальні криві над простим полем ,  визначаються як криві з порядком  й, відповідно, слідом Фробеніуса . Такі криві виявилися криптографічно слабкими, тому що порядки групи  й адитивної групи поля  рівні, що дозволяє порівняно просто побудувати атаку ізоморфізму, що переводить точки кривої в елементи групи . Цей метод уперше був запропонований І. Семаєвим, а також незалежно авторами Т. Сатохом, К. Араки й Н. Смартом. Складність  при цій атаці стає поліноміальною, що робить аномальні криві даного типу неприйнятними в криптографії.

5. - атака

Під час вивчення властивостей суперсингулярних кривих виявилося, що порядок групи  над полем  ділить порядок мультиплікативної групи розширень  або . Це дозволяє побудувати ізоморфізм між елементами групи E й мультиплікативної групи розширеного поля, після чого розв’язувати більше просту задачу визначення дискретного логарифма в полі. Ця атака ізоморфізму заснована на використанні ²спарювання Вейля² і була запропонована А. Менезисом , Т. Окамото й С. Ванстоном, у зв'язку із чим називається - атакою.

Суперсингулярні криві над полем  при непарних розширеннях  мають три класи ізоморфізму, зображених у таблиці 3 з порядками , , .

Таблиця 3 - Порядки суперсингулярних кривих над полем при непарних степенях

Крива		Порядок
	Непарне

Для кривої  з порядком  ізоморфізм існує вже при розширенні , тому що мультиплікативна група цього поля має порядок . Для інших кривих ізоморфізм виникає при розширенні , тому що  й, отже,  ділить порядок  мультиплікативної групи поля . Оскільки відомі субекспоненційні алгоритми розв’язання  в полі, такі розширення порівняно невеликі й роблять атаку успішною. У цьому зв'язку суперсингулярні криві не рекомендуються в криптографічних стандартах.

Несурперсингулярні криві й криві над простими полями також проходять тест на - атаку. Тест на стійкість до цієї атаки можна рахувати успішним, якщо порядок   не ділить порядок мультиплікативної групи розширення , рівний , для всіх розширень  Верхня межа безпеки звичайно приймається рівною