Навигация
Відзначити ці крапки на числовій прямій
2. Відзначити ці крапки на числовій прямій.
3. Розглядаємо рівняння на кожному із проміжків і встановлюємо знак виражень, які перебувають під модулями.
1) При ![]() або
або ![]() . Щоб визначити знак кожного з виражень під модулем на цьому проміжку, досить взяти будь-яке значення
. Щоб визначити знак кожного з виражень під модулем на цьому проміжку, досить взяти будь-яке значення ![]() із цього проміжку й підставити у вираження. Якщо отримане значення негативно, виходить, при всіх
із цього проміжку й підставити у вираження. Якщо отримане значення негативно, виходить, при всіх ![]() із цього проміжку вираження буде негативним; якщо отримане числове значення позитивно, виходить, при всіх значеннях
із цього проміжку вираження буде негативним; якщо отримане числове значення позитивно, виходить, при всіх значеннях ![]() із цього проміжку вираження буде позитивним.
із цього проміжку вираження буде позитивним.
Візьмемо значення ![]() із проміжку
із проміжку ![]() й підставимо його значення у вираження
й підставимо його значення у вираження ![]() , одержуємо
, одержуємо ![]() , значить на цьому проміжку
, значить на цьому проміжку ![]() негативно, а отже ``вийде'' з під модуля зі знаком ``мінус'', одержимо:
негативно, а отже ``вийде'' з під модуля зі знаком ``мінус'', одержимо: ![]() .
.
При цьому значенні ![]() , вираження
, вираження ![]() одержить значення
одержить значення ![]() , виходить, воно на проміжку
, виходить, воно на проміжку ![]() також приймає негативні значення й ``вийде'' з модуля зі знаком ``мінус'', одержимо:
також приймає негативні значення й ``вийде'' з модуля зі знаком ``мінус'', одержимо: ![]() .
.
Вираження ![]() одержить значення
одержить значення ![]() й ``вийде'' з під модуля зі знаком ``мінус'':
й ``вийде'' з під модуля зі знаком ``мінус'': ![]() .
.
Рівняння на цьому проміжку вийде таким: ![]() , вирішуючи його, знаходимо:
, вирішуючи його, знаходимо: ![]() .
.
З'ясовуємо, чи входить це значення в проміжок ![]() . Виявляється входить, значить
. Виявляється входить, значить ![]() є коренем рівняння.
є коренем рівняння.
2) При ![]() . Вибираємо будь-яке значення
. Вибираємо будь-яке значення ![]() із цього проміжку. Нехай
із цього проміжку. Нехай ![]() . Визначаємо знак кожного з виражень під модулем при цьому значенні
. Визначаємо знак кожного з виражень під модулем при цьому значенні ![]() . Виявляється, що вираження
. Виявляється, що вираження ![]() позитивно, а два інших негативні.
позитивно, а два інших негативні.
Рівняння на цьому проміжку прийме вид: ![]() . Вирішуючи його, знаходимо
. Вирішуючи його, знаходимо ![]() . Це значення не входить у проміжок
. Це значення не входить у проміжок ![]() , а виходить, не є коренем рівняння.
, а виходить, не є коренем рівняння.
3) При ![]() . Вибираємо довільне значення
. Вибираємо довільне значення ![]() із цього проміжку, скажемо,
із цього проміжку, скажемо, ![]() і підставляємо в кожне з виражень. Знаходимо, що вираження
і підставляємо в кожне з виражень. Знаходимо, що вираження ![]() й
й ![]() позитивні, а
позитивні, а ![]() --- негативно. Одержимо наступне рівняння:
--- негативно. Одержимо наступне рівняння: ![]() .
.
Після перетворення, одержимо: ![]() , а виходить, рівняння не має корінь на цьому проміжку.
, а виходить, рівняння не має корінь на цьому проміжку.
4) При ![]() . Неважко встановити, що всі вираження на цьому проміжку позитивні, а значить одержимо рівняння:
. Неважко встановити, що всі вираження на цьому проміжку позитивні, а значить одержимо рівняння: ![]() ,
, ![]() ,
, ![]() що входить у проміжок і є коренем рівняння.
що входить у проміжок і є коренем рівняння.
Відповідь. ![]() ,
, ![]() .
.
Приклад Вирішити рівняння
![]()
Рішення.
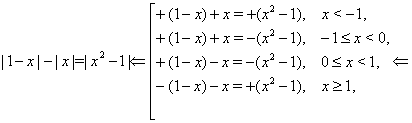
Відповідь. ![]() ,
, ![]() .
.
Використання тотожності ![]() , при рішенні рівнянь
, при рішенні рівнянь
Зі сформульованої властивості модуля можна вивести два корисних наслідки:
![]()
![]()
Проілюструємо застосування першого з них для рішення задачі вступного іспиту в Санкт-Петербурзький державний університет.
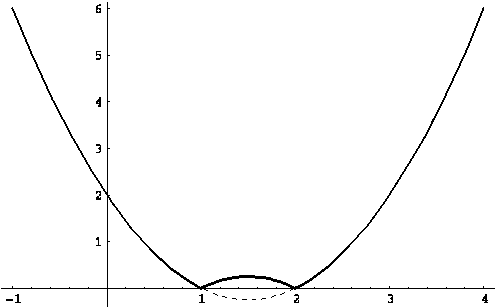
Приклад Зобразити графік функції
![]()
Рішення. Перепишемо функцію, що задає, вираження, використовуючи перший наслідок:
![]() .
.
Залишилося тільки побудувати графіки функцій ![]() ,
, ![]() в одній системі координат і визначити ділянки, на яких один з них вище іншого (див. мал. (??)).
в одній системі координат і визначити ділянки, на яких один з них вище іншого (див. мал. (??)).
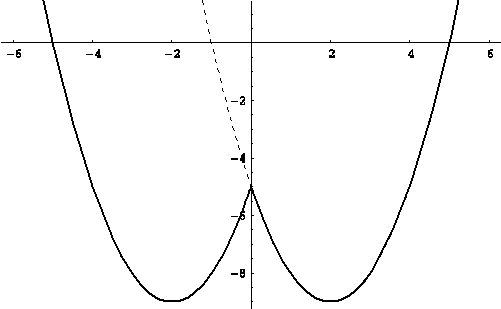
Використання другої тотожності зручно для побудови графіка функції
![]() .
.
Рішення. У силу другої тотожності, вираження, яке задає функцію, записується у вигляді: ![]() .
.
Шуканий графік зображений на малюнку (див. мал. (??)).
Приклад Знайдіть максимальне значення вираження
![]()
де ![]() ,
, ![]() , ...,
, ..., ![]() --- різні натуральні числа від 1 до 1990.
--- різні натуральні числа від 1 до 1990.
Рішення. Помітимо, що модуль різниці двох ненегативних чисел не більше їхнього максимуму. Тому ![]() не більше, ніж
не більше, ніж ![]() ,
, ![]() не більше, ніж
не більше, ніж ![]() ,
, ![]() не більше, ніж
не більше, ніж ![]() . Далі, дане вираження не може рівнятися 1990, оскільки парність цього вираження збігається з парністю суми
. Далі, дане вираження не може рівнятися 1990, оскільки парність цього вираження збігається з парністю суми ![]() . Нарешті приведемо приклад, що показує, що значення вираження може рівнятися 1989:
. Нарешті приведемо приклад, що показує, що значення вираження може рівнятися 1989:
![]()
Відповідь. 1989.
Рішення рівнянь утримуючі модулі ненегативних виражень
Приклад Чому дорівнює сума корінь рівняння (корінь, якщо він один) рівняння
![]()
Рішення. Розглянемо вираження
![]()
і перетворимо його до виду
![]()
Очевидно, що чисельник дробу при будь-яких значеннях змінної є позитивним числом. Значить дробове вираження позитивно, якщо ![]() (тому що
(тому що ![]() ). Перетворимо отримане вираження, за умови
). Перетворимо отримане вираження, за умови ![]() . Одержимо рівняння, рівносильне вихідному:
. Одержимо рівняння, рівносильне вихідному:
![]()
![]()
Відповідь. ![]() .
.
Приклад Вирішити рівняння
![]()
Рішення. Оскільки ліва частина рівняння ненегативна, при всіх припустимих значеннях змінної, на множині корінь рівняння права його частина теж повинна бути ненегативної, звідси умову ![]() , на цьому проміжку знаменники обох дробів рівні, і залишається вирішити рівняння
, на цьому проміжку знаменники обох дробів рівні, і залишається вирішити рівняння ![]() . Вирішуючи його й з огляду на обмеження
. Вирішуючи його й з огляду на обмеження ![]() , одержуємо
, одержуємо
Відповідь. ![]() .
.
Приклад Вирішити рівняння:
![]()
Рішення. Неважко догадатися, що всі вираження, що коштують під знаками другого, третього й т.д. модулів, позитивні. І оскільки модуль позитивного вираження дорівнює самому цьому вираженню, одержимо
![]()
![]()
Відповідь. ![]() .
.
Рішення рівнянь із використанням геометричної інтерпретації
Геометричний зміст вираження ![]() --- довжина відрізка координатної осі, що з'єднує крапки з абсцисами
--- довжина відрізка координатної осі, що з'єднує крапки з абсцисами ![]() й
й ![]() . Переклад алгебраїчної задачі на геометричну мову часто дозволяє уникнути громіздких викладень.
. Переклад алгебраїчної задачі на геометричну мову часто дозволяє уникнути громіздких викладень.
Приклад Вирішимо рівняння
![]() .
.
Рішення. Будемо міркувати в такий спосіб: виходячи з геометричної інтерпретації модуля, ліва частина рівняння являє собою суму відстаней від деякої крапки з абсцисою ![]() до двох фіксованих крапок з абсцисами 1 і 2. Тоді всі крапки з абсцисами з відрізка
до двох фіксованих крапок з абсцисами 1 і 2. Тоді всі крапки з абсцисами з відрізка ![]() мають необхідну властивість, а крапки, розташовані поза цим відрізком,--- немає.
мають необхідну властивість, а крапки, розташовані поза цим відрізком,--- немає.
Відповідь. ![]() .
.
Приклад Вирішимо рівняння ![]() .
.
Рішення. Міркуючи аналогічно, одержимо, що різниця відстаней до крапок з абсцисами 1 і 2 дорівнює одиниці тільки для крапок, розташованих на координатній осі правіше числа 2.
Відповідь. ![]() .
.
Приклад Вирішити нерівність ![]() .
.
Рішення. Зобразимо на координатної прямої крапки, сума відстаней від яких до крапок ![]() і
і ![]() в точності дорівнює
в точності дорівнює ![]() . Це всі крапки відрізка
. Це всі крапки відрізка ![]() . Для всіх чисел поза даним відрізком сума відстаней буде більше двох.
. Для всіх чисел поза даним відрізком сума відстаней буде більше двох.
Відповідь. ![]() .
.
Зауваження. Узагальненням рішення вищенаведених рівнянь є наступні рівносильні переходи:
![]()
Приклад Вирішите нерівність: ![]() .
.
Рішення. Вирішимо нерівність, використовуючи координатну пряму. Дана нерівність виконується для всіх крапок c координатою![]() , які перебувають ближче до крапки з координатою
, які перебувають ближче до крапки з координатою ![]() , чим до крапки з координатою
, чим до крапки з координатою ![]() . Тому що
. Тому що ![]() , те шуканими є всі крапки, розташовані лівіше крапки з координатою
, те шуканими є всі крапки, розташовані лівіше крапки з координатою ![]() .
.
Відповідь. ![]() .
.
Приклад Вирішите рівняння
![]() .
.
Рішення. Розглянемо на числовій прямій крапку з координатою ![]() . Сума
. Сума ![]() дорівнює сумі відстаней від крапки
дорівнює сумі відстаней від крапки ![]() до крапок з координатами 2, 1, 0, -1, -2. Помітимо, що сума відстаней від будь-якої крапки до крапок
до крапок з координатами 2, 1, 0, -1, -2. Помітимо, що сума відстаней від будь-якої крапки до крапок ![]() і
і ![]() не менше довжини відрізка
не менше довжини відрізка ![]() (і рівність досягається тоді й тільки тоді, коли крапка розташована на відрізку
(і рівність досягається тоді й тільки тоді, коли крапка розташована на відрізку ![]() ). Звідси одержуємо, що
). Звідси одержуємо, що ![]() не менше 4, а
не менше 4, а ![]() не менше 2 при кожному
не менше 2 при кожному ![]() . Тому для того, щоб сума
. Тому для того, щоб сума ![]() була дорівнює
була дорівнює ![]() , необхідно, щоб
, необхідно, щоб ![]() . Отже,
. Отже, ![]() необхідно дорівнює
необхідно дорівнює ![]() . Легко перевірити, що значення
. Легко перевірити, що значення ![]() дійсно є рішенням даного рівняння.
дійсно є рішенням даного рівняння.
Відповідь. ![]() .
.
Приклад Гальперин Г.О. Позитивні числа ![]() ,
, ![]() ,
, ![]() і
і ![]() такі, що система рівнянь
такі, що система рівнянь
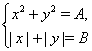
має ![]() рішень, а система рівнянь
рішень, а система рівнянь
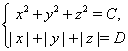
має ![]() рішень. Відомо, що
рішень. Відомо, що ![]() . Знайдіть
. Знайдіть ![]() і
і ![]() .
.
Рішення. Перше рівняння є рівняння окружності, другому задовольняють крапки квадрата із центром на початку координат і з діагоналями, що належать осям координат. Система із двох перших рівнянь залежно від ![]() і
і ![]() або не має рішень, або має чотири рішення, або вісім. Отже,
або не має рішень, або має чотири рішення, або вісім. Отже, ![]() може рівнятися або 0, або 4, або 8. Перше рівняння другої системи є рівняння сфери. Другому задовольняють крапки октаедра із центром на початку координат і з вершинами, що лежать на осях координат на рівних відстанях від центра. Ця система залежно від
може рівнятися або 0, або 4, або 8. Перше рівняння другої системи є рівняння сфери. Другому задовольняють крапки октаедра із центром на початку координат і з вершинами, що лежать на осях координат на рівних відстанях від центра. Ця система залежно від ![]() і
і ![]() або не має рішень, або має 6 рішень (вершини октаедра лежать на сфері), або має 8 рішень (сфера стосується граней октаедра), або має нескінченне число рішень (сфера перетинає грані октаедра по окружностях або декільком дугам окружностей). Отже,
або не має рішень, або має 6 рішень (вершини октаедра лежать на сфері), або має 8 рішень (сфера стосується граней октаедра), або має нескінченне число рішень (сфера перетинає грані октаедра по окружностях або декільком дугам окружностей). Отже, ![]() може рівнятися або 0, або 6, або 8, або
може рівнятися або 0, або 6, або 8, або ![]() . Умові
. Умові ![]() задовольняє тільки варіант
задовольняє тільки варіант ![]() ,
, ![]() .
.
Відповідь. ![]() ,
, ![]() .
.
Переклад алгебраїчної задачі на геометричну мову -і- зручний і потужний метод рішення задач. У якості ще одного приклада розберемо блок задач олімпіади математико-механічного факультету Спбгу:
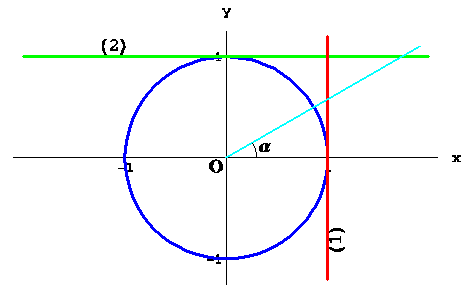
Приклад Даний функція: ![]() .
.
а) Вирішите рівняння ![]() ;
;
б) Вирішите нерівність ![]() ;
;
в) Знайдіть кількість рішень рівняння ![]() залежно від значень параметра
залежно від значень параметра ![]() .
.
Рішення. Побудуємо графік функції ![]() . Для цього помітимо, що
. Для цього помітимо, що ![]() , а тоді ми можемо спочатку побудувати графіка функції
, а тоді ми можемо спочатку побудувати графіка функції ![]() , і потім відбити його щодо осі ординат. Перетворимо вираження, що задає функцію
, і потім відбити його щодо осі ординат. Перетворимо вираження, що задає функцію ![]() :
:
![]()
Оскільки дана система визначає верхнє півколо радіуса 2 із центром у крапці (2; 0), графік вихідної функції являє собою об'єднання двох півкіл (див. мал. (??)).
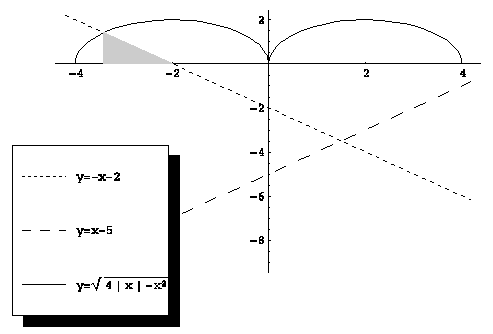
Тепер рішення задач не представляє праці:
а) Корінь рівняння є абсциса крапки перетинання прямій ![]() із графіком функції
із графіком функції ![]() . Знайдемо неї геометрично: заштрихований на малюнку прямокутний трикутник є рівнобедреним (кутовий коефіцієнт прямої дорівнює
. Знайдемо неї геометрично: заштрихований на малюнку прямокутний трикутник є рівнобедреним (кутовий коефіцієнт прямої дорівнює ![]() ), його гіпотенуза є радіус окружності, її довжина 2. Тоді довжина катета, що лежить на осі абсцис, є
), його гіпотенуза є радіус окружності, її довжина 2. Тоді довжина катета, що лежить на осі абсцис, є ![]() , а шукана абсциса дорівнює
, а шукана абсциса дорівнює ![]() .
.
б) Нерівність ![]() виконана при всіх
виконана при всіх ![]() з відрізка
з відрізка ![]() .
.
в) При ![]() ,
, ![]() рішень ні, при
рішень ні, при ![]() рівняння
рівняння ![]() має три рішення, при
має три рішення, при ![]() --- чотири рішення, при
--- чотири рішення, при ![]() --- два рішення.
--- два рішення.
Рішення рівнянь із використанням тотожності ![]()
Приклад Вирішити рівняння
![]()
Рішення. Двічі застосовуючи тотожність ![]() , одержимо рівняння
, одержимо рівняння
![]()
рішенням якого є інтервал ![]() .
.
Відповідь. ![]() .
.
Приклад Вирішити рівняння
![]()
Рішення.
![]()
Відповідь. ![]() .
.
Застосування теореми про знаки при рішенні рівнянь
Сформулюємо теорему, зручну при рішенні нерівностей, щодо добутків або приватних різниць модулів:
Теорема Знак різниці модулів двох виражень збігається зі знаком різниці квадратів цих виражень.
Приклад Вирішити нерівність
![]()
Рішення. Скористаємося теоремою:
![]()
Використовуючи формулу різниці квадратів, розкладемо чисельник і знаменник на множники й вирішимо отриману раціональну нерівність.
![]()
Відповідь. ![]()
Рішення рівнянь переходом до наслідку
Всі рівняння з модулями можуть бути вирішені в такий спосіб: розглянемо весь набір рівнянь, що може вийде при розкритті модулів, але не будемо виписувати відповідні проміжки. Вирішуючи кожне з отриманих рівнянь, одержимо наслідки вихідного рівняння. Залишається тільки перевірити чи не придбали ми сторонніх корінь прямої їхньою підстановкою у вихідне рівняння.
Приклад Вирішимо рівняння
![]()
Рішення. Послідовно переходячи до наслідків, одержуємо:
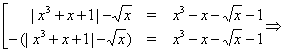
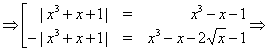
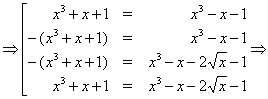
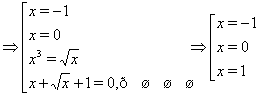
Неважко переконається, що знайдені числа не є коріннями вихідного рівняння.
Відповідь. ні рішення.
У випадку вкладених знаків модуля теж можна розглянути весь набір яких, що виходять при розкритті модуля рівнянь серед рішень, утримуються рішення вихідного рівняння, а потім відібрати із всіх отриманих рішень підходящі хоча б за допомогою перевірки.
Приклад Вирішите рівняння
![]()
Рішення. Всіх корінь вихідного рівняння втримуються серед корінь двох рівнянь
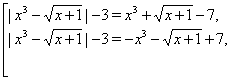
які можна переписати у вигляді
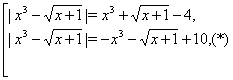
Аналогічно, кожне із цих рівнянь розпадається на два:
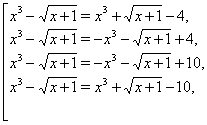
що приводить до чотирьох рівнянь:
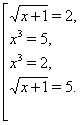
Звідси одержуємо 4 рішення: ![]() ,
, ![]() ,
, ![]() ,
, ![]() серед яких утримуються коріння вихідного рівняння. 1-й корінь, мабуть, задовольняє рівнянню. Це перевіряється легко. 2-й і 3-й не походять, тому що права частина вихідного рівняння при цих значеннях негативна. 4-й корінь теж є зайвим, тому що цей корінь повинен задовольняти рівнянню (*), а при цьому значенні його права частина негативна.
серед яких утримуються коріння вихідного рівняння. 1-й корінь, мабуть, задовольняє рівнянню. Це перевіряється легко. 2-й і 3-й не походять, тому що права частина вихідного рівняння при цих значеннях негативна. 4-й корінь теж є зайвим, тому що цей корінь повинен задовольняти рівнянню (*), а при цьому значенні його права частина негативна.
Відповідь. 3.
Рішення рівнянь методом інтервалів
Застосування методу інтервалів засновано на наступної
Теорема Функція, безперервна на проміжку, зберігає на цьому проміжку свій знак.
Це означає, що нулі функції й границі проміжків її безперервності розділяють область визначення функції на ділянки, де вона зберігає постійний знак. Застосування методу пояснимо на прикладі.
Приклад Вирішимо нерівність
![]()
Нехай ![]() . Областю визначення даної функції є
. Областю визначення даної функції є ![]() . Вирішуючи рівняння (див. (??)), одержимо, що функція
. Вирішуючи рівняння (див. (??)), одержимо, що функція ![]() не звертається в нуль ні при якому значенні змінної. Це означає, що на всій області визначення функція є знакопостійної. Обчислюючи, наприклад,
не звертається в нуль ні при якому значенні змінної. Це означає, що на всій області визначення функція є знакопостійної. Обчислюючи, наприклад, ![]() , одержуємо, що функція приймає тільки позитивні значення.
, одержуємо, що функція приймає тільки позитивні значення.
Відповідь. ![]() .
.
Метод інтервалів дозволяє вирішувати більше складні рівняння й нерівності з модулями, але в цьому випадку він має трохи інше призначення. Суть складається в наступному. Знаходимо корінь всіх підмодульних виражень і розбиваємо числову вісь на проміжки цих виражень. Це дозволяє, послідовно перебираючи ці проміжки, одночасно позбуватися від всіх модулів і вирішувати звичайне рівняння або нерівність (перевіряючи при цьому, що знайдена відповідь входить у даний проміжок).
Рішення рівнянь домноження на позитивний множник
Приклад Вирішити нерівність
![]()
Рішення. ''Пастка'' полягає в тім, що в задачі є кілька модулів, розкривати які -і значить одержати, громіздке рішення.
Помножимо дріб на деяке вираження, що приймає лише позитивні значення й таке, щоб спростити вихідна нерівність:
![]()
![]()
![]()
Відповідь. ![]() .
.
Типові тестові задачі, що містять змінну під знаком модуля
Приклад Знайти корінь рівняння
![]() .
.
Рішення. Тому що ![]() , те з рівняння треба, що
, те з рівняння треба, що ![]() ,
, ![]() . Тоді вихідне рівняння прийме вид:
. Тоді вихідне рівняння прийме вид: ![]() ,
, ![]() . Корінь цього рівняння
. Корінь цього рівняння
![]() ,
, ![]() .
.
Корінь ![]() , тому він не є рішенням, а
, тому він не є рішенням, а ![]() .
.
Відповідь. ![]() .
.
Приклад Знайти добуток корінь рівняння ![]() .
.
Рішення. Позначимо ![]() ,
, ![]() . Тоді вихідне рівняння прийме вид:
. Тоді вихідне рівняння прийме вид: ![]() . Корінь цього рівняння
. Корінь цього рівняння ![]() ,
, ![]() . Тому що
. Тому що ![]() , те
, те ![]() . Звідси
. Звідси ![]() ,
, ![]() . Добуток корінь дорівнює
. Добуток корінь дорівнює ![]() .
.
Відповідь. ![]() .
.
Приклад Знайти різницю між найбільшими й найменшими коріннями рівняння ![]() .
.
Рішення. Позначимо ![]() ,
, ![]() . Тоді вихідне рівняння прийме вид:
. Тоді вихідне рівняння прийме вид: ![]() . Вирішимо його. Корінь цього рівняння
. Вирішимо його. Корінь цього рівняння ![]() ,
, ![]() . Тому що
. Тому що ![]() , те значення
, те значення ![]() не підходить. Тому
не підходить. Тому ![]() . Різниця між найбільшим і найменшим коренями рівняння дорівнює
. Різниця між найбільшим і найменшим коренями рівняння дорівнює ![]() .
.
Відповідь. ![]() .
.
Приклад Знайти суму корінь рівняння ![]() .
.
Рішення. Використовуємо правило:
![]() .
.
Вихідне рівняння запишемо у вигляді сукупності рівнянь:
![]()
У такий спосіб сума корінь вихідного рівняння дорівнює ![]() .
.
Інший шлях. Оскільки обидві частини рівняння ненегативні, зведемо рівняння у квадрат. Одержимо: ![]() ,
, ![]() . Тому що дискримінант рівняння позитивний, то по теоремі Виета сума корінь дорівнює
. Тому що дискримінант рівняння позитивний, то по теоремі Виета сума корінь дорівнює ![]()
Відповідь. ![]() .
.
Приклад Скільки цілих корінь на відрізку ![]() має рівняння
має рівняння
![]()
Рішення. Розглянемо квадратний тричлен ![]() . Тому що
. Тому що ![]() , те
, те![]() , тому вихідне рівняння запишеться як
, тому вихідне рівняння запишеться як
![]()
![]()
Останнє рівняння еквівалентно нерівності ![]() , рішення якого
, рішення якого ![]() . Таким чином, рівняння має 6 корінь на відрізку
. Таким чином, рівняння має 6 корінь на відрізку ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Відповідь. 6.
Приклад Яке найбільше кінцеве число корінь може мати рівняння
![]()
де ![]() ,
, ![]() ,...,
,..., ![]() ,
, ![]() ,
, ![]() , ...,
, ..., ![]() --- різні числа?
--- різні числа?
Рішення. Покладемо ![]() й перепишемо вихідне рівняння у вигляді
й перепишемо вихідне рівняння у вигляді ![]() .
.
Нехай ![]() --- всі числа із множини
--- всі числа із множини ![]() , упорядковані по зростанню. На кожному з 101 проміжку
, упорядковані по зростанню. На кожному з 101 проміжку ![]() ,
, ![]() ,...,
,..., ![]() ,
, ![]() , функція
, функція ![]() лінійна. Помітимо, що на першому й останньому із цих проміжків
лінійна. Помітимо, що на першому й останньому із цих проміжків ![]() і
і ![]() відповідно, при цьому
відповідно, при цьому ![]() , тому що кількість корінь звичайно.
, тому що кількість корінь звичайно.
Підемо по числовій осі ліворуч праворуч.
Спочатку кутовий коефіцієнт функції ![]() дорівнює 0. Щораз, коли ми проходимо одну із крапок
дорівнює 0. Щораз, коли ми проходимо одну із крапок ![]() , він за рахунок зміни знака при розкритті відповідного модуля змінюється на
, він за рахунок зміни знака при розкритті відповідного модуля змінюється на ![]() .
.
Таким чином, він завжди дорівнює парному цілому числу й не може поміняти знак, не звернувшись перед цим в 0.
Виходить, кутові коефіцієнти на будь-яких двох сусідніх проміжках або обоє ненегативні, або обоє непозитивні, тобто функція ![]() на об'єднанні цих проміжків або неубутна, або незростаюча.
на об'єднанні цих проміжків або неубутна, або незростаюча.
Стало бути, якщо число її корінь звичайно, те на кожному з 50 проміжків ![]() ,...,
,..., ![]() ,
, ![]() вона має не більше одного кореня. Крім того, на крайніх інтервалах значення мають різні знаки, і в кожному корені знак функції міняється. Отже, кількість корінь парно й не перевищує 49.
вона має не більше одного кореня. Крім того, на крайніх інтервалах значення мають різні знаки, і в кожному корені знак функції міняється. Отже, кількість корінь парно й не перевищує 49.
Неважко перевірити, що якщо роль ![]() будуть грати числа 1, 4, 5, 8, 97, 100, а роль
будуть грати числа 1, 4, 5, 8, 97, 100, а роль ![]() --- числа 2, 3, 6, 7, 94, 95, 98,
--- числа 2, 3, 6, 7, 94, 95, 98, ![]() , те рівняння
, те рівняння ![]() буде мати рівно 49 корінь.
буде мати рівно 49 корінь.
Відповідь. 49.
Приклад Вирішите систему нерівностей
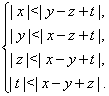
Рішення. Припустимо, що дана система нерівностей має рішення ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Тоді, зокрема,
. Тоді, зокрема, ![]() , тобто
, тобто
![]()
Аналогічно одержуємо
![]()
![]()
![]()
Перемножимо всі отримані нерівності. З одного боку, добуток чотирьох позитивних чисел позитивно. З іншого боку, цей добуток дорівнює -і-
![]()
Приходимо до протиріччя.
Відповідь. Система не має рішень.
Приклад чи Існують дійсні числа ![]() ,
, ![]() і
і ![]() такі, що при всіх дійсних
такі, що при всіх дійсних ![]() і
і ![]() виконується нерівність
виконується нерівність
![]()
Рішення. Припустимо, що такі числа ![]() ,
, ![]() і
і ![]() існують. Виберемо
існують. Виберемо ![]() й
й ![]() такі, що
такі, що ![]() ,
, ![]() ,
, ![]() . Тоді різниця між лівою й правою частинами дорівнює
. Тоді різниця між лівою й правою частинами дорівнює ![]() . А якщо взяти
. А якщо взяти ![]() й
й ![]() такі, що
такі, що ![]() ,
, ![]() ,
, ![]() , те ця різниця буде дорівнює
, те ця різниця буде дорівнює ![]() . Таким чином, з одного боку,
. Таким чином, з одного боку, ![]() , з іншої
, з іншої ![]() . Протиріччя.
. Протиріччя.
Відповідь. Немає.
Приклад Скільки різних цілочисленних рішень має нерівність ![]() ?
?
Рішення. При натуральному ![]() рівняння
рівняння ![]() має рівно
має рівно ![]() цілочисленних рішень, а при
цілочисленних рішень, а при ![]() рішення єдине. Таким чином, кількість рішень вихідної нерівності дорівнює
рішення єдине. Таким чином, кількість рішень вихідної нерівності дорівнює ![]() .
.
Відповідь. 19801.
Приклад Знайдіть всі значення параметра ![]() , при кожному з яких рівняння має три різних корені; знайдіть цих корінь:
, при кожному з яких рівняння має три різних корені; знайдіть цих корінь: ![]() .
.
Рішення. Зведемо обидві частини рівняння у квадрат: ![]() .
.
Якщо ![]() , тоді одержимо рівняння:
, тоді одержимо рівняння:
![]()
Дискримінант цього рівняння дорівнює:
![]() .
.
Рівняння (1) буде мати один корінь, при ![]() й
й ![]() . Два корені, при
. Два корені, при ![]() й
й ![]() .
.
Якщо ![]() , тоді одержимо рівняння:
, тоді одержимо рівняння:
![]()
Дискримінант цього рівняння дорівнює:
![]() .
.
Рівняння (2) буде мати один корінь при ![]() й
й ![]() . Два корені --- при
. Два корені --- при ![]() й
й ![]() .
.
Робимо висновок, що при ![]() рівняння (1) має один корінь, а рівняння (2) --- два корені. При
рівняння (1) має один корінь, а рівняння (2) --- два корені. При ![]() , рівняння (1) має два корені, а рівняння (2) --- один.
, рівняння (1) має два корені, а рівняння (2) --- один.
Таким чином, при ![]() й
й ![]() дане рівняння має три корені.
дане рівняння має три корені.
Знайдемо цих корінь. При ![]() , перше рівняння прийме вид:
, перше рівняння прийме вид: ![]() . Воно має один корінь:
. Воно має один корінь: ![]()
Рівняння (2) прикмет вид: ![]() яке має два корені:
яке має два корені: ![]() ,
, ![]() .
.
При ![]() , рівняння (2) прикмет вид:
, рівняння (2) прикмет вид: ![]() . Воно має один корінь:
. Воно має один корінь: ![]() .
.
Рівняння (1) при цьому стане: ![]() , що буде мати корінь:
, що буде мати корінь: ![]() ,
, ![]() .
.
Відповідь. При ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
При ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Приклад Для кожного значення параметра ![]() визначите число рішень рівняння
визначите число рішень рівняння ![]() .
.
Рішення.
1. Якщо ![]() , тоді рівняння не має рішень, модуль будь-якого речовинного числа ненегативний.
, тоді рівняння не має рішень, модуль будь-якого речовинного числа ненегативний.
2. Якщо ![]() , тоді одержимо рівняння
, тоді одержимо рівняння ![]() . Це рівняння має два корені, тому що
. Це рівняння має два корені, тому що ![]() .
.
3. Якщо ![]() , тоді одержуємо сукупність двох рівнянь:
, тоді одержуємо сукупність двох рівнянь:
![]()
![]()
Перше рівняння має дискримінант: ![]() . Воно не буде мати корінь при
. Воно не буде мати корінь при ![]() ,
, ![]() , але це неможливо, тому що
, але це неможливо, тому що ![]() . Також воно не може мати один корінь (тоді
. Також воно не може мати один корінь (тоді ![]() , що також неможливо). Таким чином, при
, що також неможливо). Таким чином, при ![]() рівняння (1) має два корені.
рівняння (1) має два корені.
Друге рівняння має дискримінант:
![]() .
.
Воно не буде мати корінь, якщо ![]() ,
, ![]() ,
, ![]() . Буде мати один корінь, якщо
. Буде мати один корінь, якщо ![]() . Буде мати два корені, якщо
. Буде мати два корені, якщо ![]() .
.
Остаточно одержуємо.
Відповідь. Якщо ![]() , тоді рівняння не має корінь.
, тоді рівняння не має корінь.
Якщо ![]() й
й ![]() , тоді рівняння має два корені.
, тоді рівняння має два корені.
Якщо ![]() , тоді рівняння має три корені.
, тоді рівняння має три корені.
Якщо ![]() , тоді рівняння має чотири корені.
, тоді рівняння має чотири корені.
Приклад Знайдіть всі значення параметра ![]() із проміжку
із проміжку ![]() , при кожному з яких більший з корінь рівняння
, при кожному з яких більший з корінь рівняння ![]() приймає найбільше значення.
приймає найбільше значення.
Рішення.
Перетворимо рівняння до виду
![]() .
.
Виходить, якщо
![]() ,
, ![]() ,
,
тоді ![]() .
.
Знайдемо найбільше значення ![]() , при якому
, при якому ![]() , тобто найбільше рішення нерівності
, тобто найбільше рішення нерівності
![]() .
.
Перетворимо цю нерівність:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Останню нерівність вирішимо методом інтервалів, пам'ятаючи, що ![]() .
.
Рішення нерівності буде множина: ![]() .
.
Ясно, що дріб
![]()
приймає найбільше значення при ![]() , тоді значення
, тоді значення ![]() буде дорівнює:
буде дорівнює:
![]() .
.
Відповідь. При ![]() .
.
Приклад Знайти всі значення параметра ![]() , при кожному з яких рівняння
, при кожному з яких рівняння ![]() має єдине рішення.
має єдине рішення.
Рішення.
Знайдемо рішення для кожного значення ![]() , а потім відберемо ті, які задовольняють умові задачі, тобто при яких рівняння має єдине рішення.
, а потім відберемо ті, які задовольняють умові задачі, тобто при яких рівняння має єдине рішення.
Для кожного фіксованого ![]() будемо шукати рішення даного рівняння спочатку на проміжку
будемо шукати рішення даного рівняння спочатку на проміжку ![]() , а потім на проміжку
, а потім на проміжку ![]() , оскільки модуль звертається в нуль при
, оскільки модуль звертається в нуль при ![]() :
:
1) Нехай ![]() . На цьому проміжку
. На цьому проміжку ![]() й тому дане рівняння прикмет вид
й тому дане рівняння прикмет вид ![]() .
.
Знайдемо дискримінант отриманого наведеного квадратного рівняння
![]() , виходить, при будь-якому дійсному значенні
, виходить, при будь-якому дійсному значенні ![]() рівняння має два різних дійсних корені:
рівняння має два різних дійсних корені: ![]() і
і ![]() .
.
З'ясуємо, чи входять вони в проміжок ![]() . Корінь
. Корінь ![]() лежить у цій області тільки тоді, коли виконується нерівність:
лежить у цій області тільки тоді, коли виконується нерівність: ![]() або
або ![]() .
.
Остання нерівність рівносильна системі нерівностей:
![]()
Остання система нерівностей не має рішень, виходить, ні при якому значенні параметра a число ![]() не лежить в області
не лежить в області ![]() .
.
Корінь ![]() лежить у розглянутій області тоді, коли виконана нерівність:
лежить у розглянутій області тоді, коли виконана нерівність: ![]() або
або ![]() .
.
Вирішимо останню нерівність. Ясно, що цій нерівності задовольняють всі значення ![]() із проміжку
із проміжку ![]() .
.
При ![]() одержимо нерівність
одержимо нерівність ![]() . Звідси знаходимо:
. Звідси знаходимо: ![]() .
.
Таким чином, при ![]() рівняння має єдине рішення
рівняння має єдине рішення ![]() .
.
2) Нехай ![]() . На цьому проміжку
. На цьому проміжку ![]() й тому вихідне рівняння можна переписати у вигляді
й тому вихідне рівняння можна переписати у вигляді ![]() . Знайдемо дискримінант цього рівняння:
. Знайдемо дискримінант цього рівняння: ![]() .
.
Рівняння не має рішень, якщо ![]() , тобто якщо
, тобто якщо ![]() .
.
Виходить, рівняння не має корінь для ![]() із проміжку
із проміжку ![]() .
.
Якщо ![]() не належать цьому проміжку, то квадратне рівняння має коріння
не належать цьому проміжку, то квадратне рівняння має коріння ![]() ,
, ![]() , причому
, причому ![]() при
при ![]() й
й ![]() . З'ясуємо тепер, при яких значеннях параметра
. З'ясуємо тепер, при яких значеннях параметра ![]() знайдених корінь лежать в області
знайдених корінь лежать в області ![]() .
.
Для цього потрібно вирішити нерівності ![]() й
й ![]() .
.
Нерівність ![]() рівносильна нерівності
рівносильна нерівності ![]() або сукупності двох систем нерівностей:
або сукупності двох систем нерівностей:
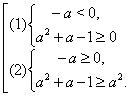
Множина рішень першої системи має вигляд ![]() , друга система не має рішень. Виходить, тільки при значенні
, друга система не має рішень. Виходить, тільки при значенні ![]() корінь рівняння
корінь рівняння ![]() лежить в області
лежить в області ![]()
Нерівність ![]() рівносильна нерівності
рівносильна нерівності ![]() або системі нерівностей
або системі нерівностей
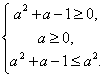
Множина рішень отриманої системи нерівностей є відрізок ![]() .
.
Тільки при цих значеннях параметра ![]() , корінь
, корінь ![]() належить області:
належить області: ![]() . Таким чином, при
. Таким чином, при ![]() дане рівняння в області
дане рівняння в області ![]() рішень не має.
рішень не має.
Якщо ![]() , то рівняння в розглянутій області має єдине рішення
, то рівняння в розглянутій області має єдине рішення ![]() .
.
При значеннях ![]() , що лежать в області
, що лежать в області ![]() вихідне рівняння має два різних корені
вихідне рівняння має два різних корені ![]() й
й ![]() . Якщо ж
. Якщо ж ![]() , то вихідне рівняння має єдиний корінь
, то вихідне рівняння має єдиний корінь ![]() . Отримані результати зручно звести в таблицю:
. Отримані результати зручно звести в таблицю:
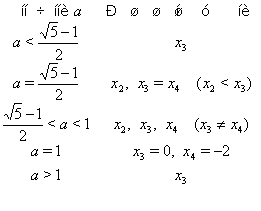
Таким чином, шукані значення ![]() утворять два проміжки:
утворять два проміжки: ![]() і
і ![]() .
.
Відповідь. ![]() ,
, ![]() .
.
Приклад Знайти всіх корінь рівняння ![]() , що задовольняє нерівності
, що задовольняє нерівності ![]() .
.
Рішення. Будуємо графіки функцій ![]() і
і ![]() . Одержимо дві крапки перетинання, абсциса тільки однієї з них менше
. Одержимо дві крапки перетинання, абсциса тільки однієї з них менше ![]() , тобто задовольняє умови задачі
, тобто задовольняє умови задачі
Абсцису крапки можна одержати вирішивши рівняння ![]() .
.
Відповідь. ![]() .
.
Приклад Вирішити аналітично й графічно рівняння
![]()
Аналітичне рішення
Перетворимо рівняння, помноживши обидві його частини на 2, будучи позитивним числом, його можна вносити під знак модуля, тому одержимо:
![]()
У кожного із тричленів позитивні дискримінанти. Це дає можливість розкласти кожний з них на лінійні множники.
Рівняння прийме вид: ![]() .
.
На числовій прямій відкладемо крапки, у яких кожний із множників звертається в нуль. У результаті одержимо п'ять проміжків, на кожному з яких визначимо знаки тричленів під модулем і вирішимо отримані рівняння.
Однак такий спосіб не буде раціональним. Доцільніше зобразити проміжки кожного із тричленів на числових осях. Тоді визначення їхніх знаків буде спрощене й зробиться більше наочним
При такому схематичному зображенні зрозуміло, що:
1) при ![]() обидва тричлени позитивні й рівняння прийме вид:
обидва тричлени позитивні й рівняння прийме вид:
![]()
Вирішуючи його, знаходимо ![]() ,
, ![]() . Обидва корені не входять у проміжок
. Обидва корені не входять у проміжок ![]() і є сторонніми;
і є сторонніми;
2) при ![]() перший тричлен негативний, а другий позитивний, одержимо рівняння:
перший тричлен негативний, а другий позитивний, одержимо рівняння: ![]() звідки знаходимо корінь
звідки знаходимо корінь ![]() , що входить у проміжок
, що входить у проміжок ![]() і є рішенням рівняння;
і є рішенням рівняння;
3) при ![]() обидва тричлени негативні, одержуємо:
обидва тричлени негативні, одержуємо:
![]() , звідки
, звідки ![]() , що входить у проміжок
, що входить у проміжок ![]() і є рішенням рівняння;
і є рішенням рівняння;
4) при ![]() перший тричлен позитивний, другий --- негативний, одержуємо рівняння:
перший тричлен позитивний, другий --- негативний, одержуємо рівняння:
![]() , звідси
, звідси ![]() , що входить у проміжок
, що входить у проміжок ![]() і є рішенням рівняння;
і є рішенням рівняння;
5) при ![]() обидва тричлени позитивні, виходить така ж ситуація, як і в першому випадку. І тут, обидва корені
обидва тричлени позитивні, виходить така ж ситуація, як і в першому випадку. І тут, обидва корені ![]() ,
, ![]() не входять у проміжок і є сторонніми.
не входять у проміжок і є сторонніми.
Відповідь. ![]() ,
, ![]() ,
, ![]() .
.
Графічне рішення
Для графічного рішення перетворимо рівняння:
![]()
![]()
Побудуємо графіки функцій
![]() і
і ![]()
Графік функції
![]()
будемо будувати в кілька етапів:
а) будуємо графік функції
![]() ;
;
б) будуємо графік функції
![]() , `
, `
дзеркально'' відбивши нижню частину кривої
![]() в осі
в осі ![]() ;
;
в) будуємо графік функції
![]()
для цього досить графік функції ![]() ``опустити'' долілиць (здійснити паралельний перенос уздовж осі
``опустити'' долілиць (здійснити паралельний перенос уздовж осі ![]() ) на
) на ![]() ;
;
г) отриманий графік повністю симетрично відіб'ємо в осі ![]() , ``перевернемо'' навколо осі
, ``перевернемо'' навколо осі ![]() на
на ![]() .
.
У результаті одержимо графік функції
![]() .
.
Графік функції
![]()
побудуємо вже відомим способом: будуємо параболу ![]() й дзеркально відбиваємо в осі
й дзеркально відбиваємо в осі ![]() тільки частина параболи, що перебуває нижче осі
тільки частина параболи, що перебуває нижче осі ![]() .
.
Знаходимо абсциси крапок перетинання графіків, які й будуть рішеннями рівняння
Абсциси крапок перетинання наступні: 1,75; 2,5 і 3,25. Вони й будуть рішеннями рівняння.
Приклад Вирішите рівняння ![]() .
.
Рішення. Вирішувати будемо це рівняння послідовне ``розкриваючи'' модулі, починаючи з ``зовнішнього'' і ``наближаючись'' до змінного ![]() .
.
Після розкриття першого модуля, одержимо сукупність двох рівнянь:
(1) ![]() або (2)
або (2) ![]() .
.
Вирішуючи рівняння (1), у свою чергу, одержуємо два рівняння:
![]() ,
,
(3) ![]() або (4)
або (4) ![]() .
.
З рівняння (3) знаходимо: ![]() ,
, ![]() з рівняння (4) знаходимо:
з рівняння (4) знаходимо: ![]() ,
, ![]()
Вирішуючи рівняння (2), також одержимо: ![]() , що розпадається два рівняння:
, що розпадається два рівняння:
(![]() )
) ![]() або (
або (![]() )
) ![]() .
.
З (![]() ) одержуємо:
) одержуємо:
![]() ,
, ![]() ,
, ![]() З (
З (![]() )
) ![]() , що не має рішень.
, що не має рішень.
Відповідь. ![]()
Приклад Вирішити рівняння:
![]()
Рішення. ОДЗ даного рівняння:
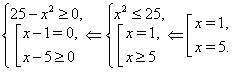
Простою перевіркою неважко переконатися, що ![]() й
й ![]() --- рішення даного рівняння.
--- рішення даного рівняння.
Відповідь. ![]() .
.
Якщо вирішувати рівняння шляхом піднесення у квадрати обох його частин, то вийде рівняння
![]()
У цього рівняння додасться ``зайвий'' корінь ![]() , що не належить ОДЗ.
, що не належить ОДЗ.
Перетворення ![]() , не рівносильне, тому що
, не рівносильне, тому що ![]() входить в ОДЗ вихідного вираження, але не входить в ОДЗ перетвореного.
входить в ОДЗ вихідного вираження, але не входить в ОДЗ перетвореного.
Нюанс полягає в тому, що при ![]() функція
функція ![]() існує й при
існує й при ![]() , тому що на що нуль не множ --- буде нуль.
, тому що на що нуль не множ --- буде нуль.
Приклад Вирішити рівняння ![]() .
.
Рішення. Почнемо розкривати внутрішній модуль (розкриття зовнішнього модуля займе набагато більше часу):
1. При ![]() маємо
маємо ![]() .
.
Тепер розглянемо два випадки:
а) ![]() , тобто
, тобто ![]() ;
;
б) ![]() і
і ![]()
Так як функція, що стає в першій частині вихідного рівняння, --- парна, то рішенням так само буде ![]() й
й ![]() .
.
Відповідь. ![]() .
.
Приклад Чому дорівнює сума корінь рівняння (корінь, якщо він один) рівняння
![]()
Рішення. Розглянемо вираження
![]()
і перетворимо його до виду
![]()
Очевидно, що чисельник дробу при будь-яких значеннях змінної є позитивним числом. Значить дробове вираження позитивно, якщо ![]() (тому що
(тому що ![]() ). Перетворимо отримане вираження, за умови
). Перетворимо отримане вираження, за умови ![]() . Одержимо рівняння, рівносильне вихідному:
. Одержимо рівняння, рівносильне вихідному:
![]()
![]()
Відповідь. ![]() .
.
Приклад Всі значення квадратного тричлена ![]() на відрізку
на відрізку ![]() по модулі не перевершують 1. Яке найбільше значення при цьому може мати величина
по модулі не перевершують 1. Яке найбільше значення при цьому може мати величина ![]() ?
?
Відповідь. Максимальне значення величини ![]() дорівнює 17.
дорівнює 17.
Доведемо це. Спочатку доведемо, що ця величина не може бути більше 17. Тому що значення тричлена ![]() на відрізку
на відрізку ![]() по модулі не перевершують одиниці, те
по модулі не перевершують одиниці, те![]() ,
, ![]() ,
, ![]() , тобто
, тобто ![]() ,
, ![]() ,
, ![]() . Тому що модуль суми не перевершує суми модулів, те
. Тому що модуль суми не перевершує суми модулів, те
![]()
![]()
Отже, ![]() . Залишилося помітити, що квадратний тричлен
. Залишилося помітити, що квадратний тричлен ![]() задовольняє умові задачі й для нього величина
задовольняє умові задачі й для нього величина ![]() дорівнює 17.
дорівнює 17.
Приклад Знайдіть найбільше ціле значення параметра ![]() , при якому рівняння
, при якому рівняння ![]() не має рішень.
не має рішень.
Рішення. Вихідне рівняння рівносильне рівнянню
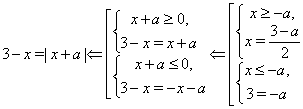
Друга система має рішення тільки при ![]() (при цьому її рішеннями будуть усе
(при цьому її рішеннями будуть усе ![]() ). Перша система не має рішень, якщо
). Перша система не має рішень, якщо ![]() При цьому найбільше ціле
При цьому найбільше ціле![]() , мабуть, дорівнює
, мабуть, дорівнює ![]() .
.
Відповідь. ![]() .
.
Висновок
абсолютна величина модуль теорема
Матеріал даної дипломної роботи адресований учителям математики, викладачам підготовчих курсів, школярам і абітурієнтам. Розглянуто властивості абсолютних величин, наведені теореми про рівносильні перетворення рівнянь і нерівностей, що містять знак модуля. Сформульовано маловідомі твердження, що істотно спрощують традиційні алгоритмічні способи рішення шкільних, конкурсних задач. Теоретичний матеріал проілюстрований значною кількістю завдань (більше 80) із вступних іспитів, математичних олімпіад і завдань незалежного оцінювання знань.
Список джерел
[1] Веременок В. В., Практикум по математиці, підготовка до тестування й іспитів. – К., 2008
[2] Д. Гущин, Потужне рішення. Рівняння й нерівності з модулями //Учительська газета №39.
[3] В.Голубєв Школа рішення нестандартних задач. Заняття 3. Нестандартна техніка рішення нерівностей з модулем // Математика №5, 2005 с. 24--31.
[4] В.Голубєв, Школа рішення нестандартних задач. Заняття 5. Сума модулів// Математика № 12, 2005 с.41--48.
[5] Тишин В. И., Математика для вчителів і учнів: раціональні алгебраїчні рівняння. – К., 2005
[6] О. Ігудисман, Математика на усному іспиті. – К., 2006
[7] Куланін Е.Д., 3000 конкурсних задач по математиці. – К., 2005
Похожие работы
... допомогою цієї програми учень може сам перевіряти набуті знання, і вчитель може перевіряти знання певного учня. Вступ. МЕТА РОБОТИ - системазувати відомості про показникові та логарифмічні рівняння й нерівності та їх системи в шкільному курсі алгебри старшої школи і розкрити роль і місце вивчення показникових та логарифмічних рівняньта нерівностей в школі та вибрати методику подання цієї теми. ...
... , рівняння прийме вид: Очевидно, що , для всіх і Отже, останнє рівняння рівносильне системі: Тим самим, ми довели, що при , рівняння має єдине рішення. Відповідь. . тригонометричний рівняння комбінований графічний Рішення з дослідженням функції Приклад [??] Доведіть, що всі рішення рівняння і- цілі числа. Рішення. Основний період вихідного рівняння дорівнює . Тому ...
... когерентність зберігається, називають довжиною когерентності. Кореляційна функція другого порядку відображає кореляцію між амплітудами світлового пучка в двох просторово-часових крапках. Когерентність другого порядку наочно просліджується в досвіді Юнга. Зв'язок теоретичного опису когерентності другого порядку з даними інтерференційних вимірів дає комплексна міра когерентності, нормована величина ...
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...



0 комментариев