Навигация
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
КИРОВОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ им. Винниченка
КУРСОВАЯ РАБОТА
по курсу «Математика»
на тему : «Нестандартный анализ»
Кировоград
2003
СОДЕРЖАНИЕ
ВСТУПЛЕНИЕ……………………………………………………………………………3
1. ЛЕЙБНИЦ И “ДРЕВНЯЯ ИСТОРИЯ” НЕСТАНДАРТНОГО АНАЛИЗА ….…4
2. РОБИНСОН И «НОВАЯ ИСТОРИЯ» НЕСТАНДАРТНОГО АНАЛИЗА……...8
3. БЕСКОНЕЧНО МАЛЫЕ ВЕЛИЧИНЫ…………………………………………….10
4. ГИПЕРДЕЙСТВИТЕЛЬНАЯ ПРЯМАЯ……………………………………………16
5. ПРИМЕР НЕАРХИМЕДОВОЙ ЧИСЛОВОЙ СИСТЕМЫ………………….……..186. НОВЫЕ ТРЕБОВАНИЯ К ГИПЕРДЕЙСТВИТЕЛЬНЫМ ЧИСЛАМ И ОСНОВНАЯ ГИПОТЕЗА………………………………………………………………21
7. СЛЕДСТВИЯ ОСНОВНОЙ ГИПОТЕЗЫ………………………………………….248. ПОСТРОЕНИЕ СИСТЕМЫ ГИПЕРДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ………………27
ЛИТЕРАТУРА………………………………………………………………………..….33
ВСТУПЛЕНИЕ
Нестандартный анализ возник в 1960 году, когда Абрахам Робинсон, специалист по теории моделей, понял, каким образом методы математической
логики позволяют оправдать классиков математического анализа XVII и XVIII вв., поставив на строгую основу их рассуждения, использующие “бесконечно большие” и бесконечно малые величины. Таким образом, речь идет не о каких-то новых “нестандартных” методах, не имеющих ничего общего с традиционной математикой, а о развитии новых средств внутри стандартной (теоретико-множественной) математики.
Нестандартный анализ остался бы любопытным курьезом, если бы единственным его приложением было обоснование рассуждений классиков математического анализа. Он оказался полезным и при развитии новых математических теорий. Нестандартный анализ можно сравнить с мостом, переброшенным через реку. Постройка моста не расширяет доступной нам территории, но сокращает путь с одного берега на другой. Подобным образом нестандартный анализ делает доказательства многих теорем короче.
Однако, быть может, главное значение нестандартного анализа состоит в другом. Язык нестандартного анализа оказался удобным средством построения математических моделей физических явлений. Идеи и методы нестандартного анализа могут стать важной частью будущей физической картины мира. Во всяком случае уже сейчас многие специалисты по математической физике активно используют нестандартный анализ в своей работе.
Нестандартный анализ позволяет с новой точки зрения посмотреть на многие рассуждения классиков математического анализа, кажущиеся нестрогими, но приводящие к успеху, и путем относительно небольших уточнений сделать их удовлетворяющими современным критериям строгости.
1. ЛЕЙБНИЦ И “ДРЕВНЯЯ ИСТОРИЯ” НЕСТАНДАРТНОГО АНАЛИЗА
Возраст нестандартного анализа колеблется (в зависимости от точки зрения) от двух с половиной десятков до трех сотен лет. Два с половиной десятка получится, если считать, что нестандартный анализ зародился осенью 1960 г., когда его основатель, Абрахам Робинсон, сделал доклад на одном нз семинаров Принстонского университета о возможности применения методов математической логики к обоснованию математического анализа. Триста лет получится, если считать началом нестандартного анлиза появление символов бесконечно малых dx, dy трактате Лейбница “Новый метод”.
Трудно сказать с уверенностью, насколько в действительности Лейбниц был близок к идеям нестандартного анализа. Как пишет сам Робинсон “история предмета обычно пишется в свете его позднейшего развития. Уже более чем полвека все обзоры истории дифференциального и интегрального исчислений основывались на уверенности в том, что понятие бесконечно малых и бесконечно больших, если даже и непротиворечиво, бесполезно для развития анализа. В результате в работах этого периода заметно различие между строгостью, с которой рассматриваются идеи Лейбница и его последователей, и снисходительностью, проявляемой к провозвестникам идеи предела”. Характерно, например, следующее высказывание Анри Лебега от 3 декабря 1926 г. “Бесконечно малые были когда-то туманными сущностями, встречавшимися в неясных и неточных формулировках. Все разъяснилось впоследствии благодаря понятию предела”.
Считая, что идеи Лейбница и идеи сторонников понятия предельного перехода мерились двойным стандартом при несправедливом склонении весов правосудия в пользу предела, Робинсон предлагает во многом пересмотреть общую картину возникновения и развития математического анализа от Ньютона и Лейбница до Коши и Вейерштрасса. Этот пересмотр приводит к более полному признанию заслуг Лейбница, и сам Лейбниц перемещается, таким образом, из разряда гениев третьего класса в разряд гениев второго класса (классификация, предложенная Станиславом Лемом: в этой классификации гении третьего класса получают прижизненное, а гении более высокого класса – лишь посмертное признание).
Изложим историко-математические взгляды Робинсона. Робинсон резюмирует стандартный взгляд на историю развития математического анализа в следующих словах: “После длительного периода, в течение которого были определены площади, объемы и касательные в различных частных случаях, во второй половине семнадцатого столетия Ньютоном и (несколько позже, но независимо) Лейбницем была построена общая теория дифференцирования и интегрирования. Касаясь обоснования введенных им понятий, Ньютон обращался то к бесконечно малым, то к пределам, то непосредственно к физической интуиции; его непосредственные последователи предпочитали последнее. С другой стороны, Лейбниц и его последователи развивали теорию исходя из дифференциалов первого и следующих порядков. Технические удобства обозначений, использовавших дифференциалы, привели к быстрому развитию Анализа и его приложений в Европе, где они были приняты. Однако внутренние противоречия этой концепции привели к осознанию того, что необходимы какие-то другие основания. Лагранж считал, что ему удалось найти подходящий путь, взяв за основу тейлоровское разложение функции. Но первое строгое обоснование математического анализа было дано лишь Коши. Основой теории Коши было понятие предела, которое, будучи впервые выдвинуто Ньютоном, впоследствии поддерживалось Даламбером. Более формальное изложение методов Коши было дано Вейерштрассом (которого в некоторой степени предвосхитил Больцано). После создания теория пределов использование бесконечно больших и бесконечно малых превратилось в оборот речи, применяемый в выражениях типа “... стремится к бесконечности”. Дальнейшее развитие теории неархимедовых полей было целиком предоставлено алгебре.”
Этот стандартный вгляд, но мнению Робинсона, в некоторых отношениях “должен быть дополнен или даже изменен”. В доказательсто этого Робинсон приводит большое количество выдержек из сочинений Лейбница и других упомянутых выше авторов. Как считает Робинсон, “... отношение Лейбница к бесконечно большим и бесконечно малым величинам в Анализе в основном оставалось неизменным в течение двух последних десятилетий его жизни. Он полностью одобрял их введение, но считал их “идеальными элементами, подобными мнимым числа. Эти идеальные элементы подчиняются тем же законам, что и обычные числа. Тем не менее они представляют собой не более чем удобные фикции, необходимые для облегчения рассуждений и открытий. Всегда, при желании, можно исключить их использование и вернуться к стилю античных математиков, рассуждая в терминах величин, достаточно больших (или малых) для того, чтобы ошибка была меньше любой наперед заданной. Все это отчетливо и неоднократно утверждается в сочинениях Лейбница”.
Приведем теперь некоторые из высказываний Лейбница, цитируемых Робинсоном.
“... Нужно воспринимать бесконечное подобно тому, как это делается в оптике, когда солнечные лучи считаются приходящими из бесконечно удаленной точки и поэтому параллельными... И когда имеются различные порядки бесконечного или бесконечно малых, то понимаются они в том же смысле, в каком земной шар считается точкой по сравнению с расстоянием до неподвижных звезд, а шарик в наших руках — точкой по сравнению с радиусом земного шара, так что расстояние до неподвижных звезд является бесконечно бесконечным или бесконечностью бесконечности по отношению к диаметру шарика. Вместо бесконечно большого или бесконечно малого количества можно взять количество настолько большое или малое, насколько это нужно, чтобы ошибка не превышала заданной. Отличие от архимедовского стиля рассуждений лишь в выражениях, которые у нас более непосредственные и лучше приспособлены для искусства изобретать”.
“...Если кто-то не желает рассматривать бесконечно большие и малые в строго метафизическом смысле, как реально существующие, он можег пользоваться ими как «идеальными понятиями», которые сокращают рассуждения, подобно мнимым корням в обычном анализе... Таким же образом представляют более трех измерений...— все это для установления идей, способных сокращать рассуждения и основывающихся на реальностях.
Не следует все же воображать, что наука о бесконечном унижается этим объяснением и сводится к фикциям, ибо постоянно остается, говоря языком схоластики, синкатегорематическая бесконечность. Например, остается верным, что 2 равно 1/1+1/2+1/4+1/8+1/16+1/32 и т. д., что есть бесконечный ряд, в котором содержатся сразу все дроби с числителем 1 и со знаменателями, образующими удваивающуюся геометрическую прогрессию, хотя здесь употребляют все время лишь обыкновенные числа и хотя не вводят никакой бесконечно малой дроби или дроби с бесконечным знаменателем... Правила конечного сохраняют силу в бесконечном, как если бы существовали атомы..., хотя они вовсе не существуют, ибо материя в действительности делима без конца и, наоборот, правила бесконечного сохраняют силу в конечном, как если бы имелись метафизические бесконечно малые, хотя в них и нет нужды и хотя деление материи никогда не приходит к бесконечно малым частицам. Это объясняется тем, что все управляется разумом и что иначе совсем не было бы ни науки, ни правила, а это не согласовалось бы с природой верховного начала”. (Это высказывание Лейбница можно при желании рассматривать как формулировку принципа переноса, что дает еще одно основание называть его также “принципом Лейбница”.)
“...Несравнимыми величинами я называю такие, одна из которых никогда не сможет превзойти другую, на какое конечное число ее бы ни помножили, так же как это понимает Евклид...”.
Приведем еще несколько цитат (на этот раз отсутствующих в монографии Робинсона).
“...новый Анализ бесконечных рассматривает не линии и не числа, но величины вообще, как это делает обыкновенная Алгебра. Этот Анализ содержит новый алгоритм, т. е. новый способ складывать, вычитать, умножать, делить, извлекать корни, соответствующий несравнимым величинам, т. е. тем, которые бесконечно велики или бесконечно малы в сравнении с другими...”
Методы Лейбница господствовали в Европе в течение более чем 50 лет. Однако во второй половине XVIII столетия начались поиски альтернативных путей построения анализа. Лагранж предлагал рассматривать разложения функций в степенные ряды, предполагая, что любая или почти любая функция может быть разложена в такой ряд. Даламбер предлагал понятие предела в качестве исходного для построения математического анализа. Он писал:
“Говорят, что одна величина лявляется пределом другой, если вторая может приблизиться к первой ближе, чем на любую заданную величину... Теория пределов является основанием подлинной Метафизики дифференциального исчисления... В дифференциальном исчислении речь идет не о бесконечно малых величинах, как это обычно утверждают; речь идет лишь о переделах конечных величин... Термином “бесконечно малая» пользуются лишь как сокращением …»
Эти высказывания даламбера выглядят как изложение современной точки зрения на пределе. Можно было бы предположить, что с этого времени понятие бесконечно малых будет полностью устранено. Это, однако, не так. Коши, рассматриваемый обычно как основатель современного подхода к построению анализа, использует понятие бесконечно малой величины. Пытаясь объяснить в современных терминах, что Коши называет “величиной”, можно предположить, что величина — это функция с действительными значениями, определенная на упорядоченном множестве без наибольшего элемента. Коши, однако, отнюдь не сводит величины к функциям. Наоборот, он говорит о функции как о соотношении, связывающем две величины. В его изложении бесконечно малые и пределы фигурируют как равноправные компоненты обоснования анализа.
Похожие работы
... состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при существует, но не непрерывна. Точечного спектра оператор не имеет. Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
... динамике и соотношениям, которые связывают его с другими управляющими параметрами, характеризующими человеческое общество [7-10 ]. Можно установить непосредственную связь этого параметра с некоторой физической мерой, характеризующей как отдельного человека, так и человечество в целом, которая связывает этот биологический вид со всеми живыми и неживыми объектами природы – этой мерой является масса ...
... у детей. Дети бережнее относится к инвентарю, повышается плотность урока, повышается качество обучения. Так же при использовании такого оборудования происходит влияние на формирование интереса младшего школьного возраста на уроках физической культуры. Происходит удовлетворение интереса, который может укрепляться, развиваться, становиться более глубоким и разносторонним. Интерес, таким образом, ...
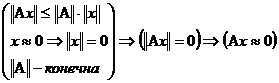
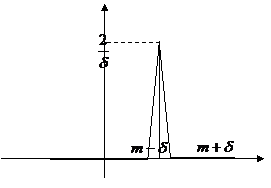

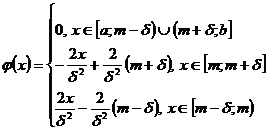


0 комментариев