Навигация
Следовательно оператор А непрерывен
4) Непрерывный оператор является ограниченным, а у ограниченного оператора есть норма, найдем норму оператора А (по определению 5):
||A|| = ![]() |Af| =
|Af| = ![]() |f(x+a)|
|f(x+a)| ![]() 1.
1.
Поскольку ||f|| = ![]() |f(x)|
|f(x)| ![]() 1.
1.
Норма А: ||A|| = 1.
5) Обратимость оператора А: Af(x) = f(x+a)
Такой оператор A сдвигает функцию на const a; обратный к A оператор будет сдвигать функцию на const (-a):
A-1f(x) = f(x-a).
6) Спектр оператора А.
Рассмотрим пространство непрерывных функций – С[0, +![]() ), имеющих конечный предел на
), имеющих конечный предел на ![]() :
:
Af(x) = f(x+a), a![]() 0.
0.
Вопрос о спектре оператора А касается разрешимости в пространствах С[0,b) и С[а,+![]() ).
).
Введем функцию V(x) = ![]() при |
при |![]() |<1,
|<1, ![]()
![]() 0, найдем ее предел:
0, найдем ее предел:
![]()
![]() = 0
= 0
Следовательно рассмотренная функция входит в пространство С[0,+![]() ).
).
Теперь рассмотрим V(x+a) = ![]() =
= ![]() *
*![]() =
= ![]() *V(x).
*V(x).
Для ![]() =0 подберем непрерывную функцию = 0 при x
=0 подберем непрерывную функцию = 0 при x ![]() а и не равную 0 при x
а и не равную 0 при x ![]() [0, a]. Для этой функции A(V(x)) = 0 то есть она является собственным вектором для числа 0; функция V(x) = с, так же удовлетворяет разностному отношению
[0, a]. Для этой функции A(V(x)) = 0 то есть она является собственным вектором для числа 0; функция V(x) = с, так же удовлетворяет разностному отношению ![]() V(x) - V(x+a) = 0. Значит
V(x) - V(x+a) = 0. Значит ![]() =1
=1 ![]() точечному спектру и в том и в другом пространстве. И все точки внутри единичного круга
точечному спектру и в том и в другом пространстве. И все точки внутри единичного круга ![]() точечному спектру.
точечному спектру.
Покажем, что остальные точки окружности ![]() точечному спектру оператора А в пространстве С[0, +
точечному спектру оператора А в пространстве С[0, +![]() ).
).
Рассмотрим U(x) = ![]() и число
и число ![]() =
= ![]() (|
(|![]() | = 1);
| = 1);
U(x+a) =  =
= ![]()
![]() =
= ![]() U(x);
U(x);
U(x) = ![]() = Cos(
= Cos(![]() ) + iSin(
) + iSin(![]() ), принадлежит пространству С[0,b) так как мнимая и действительная части – функции ограниченные, но не принадлежат пространству С[a, +
), принадлежит пространству С[0,b) так как мнимая и действительная части – функции ограниченные, но не принадлежат пространству С[a, +![]() ) так как не имеют конечного предела на
) так как не имеют конечного предела на ![]() .
.
Если точки лежат вне единичного круга, то они регулярные для оператора А в 2-х пространствах.
Покажем, что в пространстве С[0, +![]() ) точки
) точки ![]() =
= ![]() ,
, ![]()
![]() 2
2![]() n не будут собственными числами.
n не будут собственными числами.
Докажем это от противного: пусть найдется ![]() =
= ![]() ,
, ![]()
![]() 2
2![]() n – собственное число, тогда найдется функция f(x)
n – собственное число, тогда найдется функция f(x) ![]() С[0, +
С[0, +![]() ), что
), что
f(x+a) = ![]() f(x).
f(x).
Применим оператор А n раз: f(x+n*a) = ![]() nf(x), тогда
nf(x), тогда
![]() f(x+na) =
f(x+na) = ![]()
![]() nf(x), у левой части предел конечен;
nf(x), у левой части предел конечен;
правая часть предела не имеет, так как не имеет предела последовательность ![]() n =
n = ![]() = Cos(
= Cos(![]() n) + iSin(
n) + iSin(![]() n).
n).
Следовательно ![]() =
= ![]() ,
, ![]()
![]() 2
2![]() n собственным числом не является.
n собственным числом не является.
Эти точки будут принадлежать спектру оператора А в пространстве С[0,+![]() ), так как спектр замкнутое множество и граница единичного круга должна принадлежать спектру оператора А в пространстве С[0, +
), так как спектр замкнутое множество и граница единичного круга должна принадлежать спектру оператора А в пространстве С[0, +![]() ).
).
Сделаем вывод:
При |![]() |>1 все точки регулярные;
|>1 все точки регулярные;
При |![]() |<1 и
|<1 и ![]() =1 – точки спектра;
=1 – точки спектра;
При ![]() =
= ![]() ,
, ![]()
![]() 2
2![]() n – точки непрерывного спектра.
n – точки непрерывного спектра.
Вывод:
Оператор А, действующий в пространстве непрерывных и ограниченных функций – C[![]() ], заданный следующим образом: Af(x) = f(x+a), где функции f(x), f(x+a)
], заданный следующим образом: Af(x) = f(x+a), где функции f(x), f(x+a) ![]() C[
C[![]() ], a
], a ![]() R, f(x+a) – непрерывная и ограниченная функция:
R, f(x+a) – непрерывная и ограниченная функция:
1. линейный;
2. непрерывный и ограниченный;
3. норма А: ||A|| = 1;
4. A-1f(x) = f(x-a);
5. Спектр оператора А:
· при |![]() |<1 и
|<1 и ![]() =1 – точки спектра;
=1 – точки спектра;
· при ![]() =
= ![]() ,
, ![]()
![]() 2
2![]() n – точки непрерывного спектра;
n – точки непрерывного спектра;
· При |![]() |>1 все точки регулярные.
|>1 все точки регулярные.
Заключение
В ходе проделанной работы были рассмотрены основные определения теории линейных операторов: непрерывность, ограниченность, норма, спектр оператора и резольвента. Проведено исследование четыре оператора: оператор умножения на непрерывную функцию, оператор интегрирования, оператор дифференцирования, оператор сдвига. Можно сказать, что поставленные цели были достигнуты.
Список литературы
1. Колмогоров, А.Н. Элементы теории функций и функционального анализа [Текст]/ А.Н. Колмогоров, С.В. Фомин. – М.: Наука; Главная редакция физико–математической литературы, 1972.
2. Соболев, В.И. Лекции по дополнительным главам математического анализа [Текст] / В.И. Соболев. - М.: Наука, 1968.
3. Петров, В.А., Виленкин, Н.Я, Граев, М.И. Элементы функционального анализа в задачах [Текст]/ В.А. Петров, Н.Я. Виленкин, М.И. Граев под ред. О.А. Павлович. - М.: Просвещение, 1978.
4. Данфорд, Н. Линейные операторы. Общая теория [Текст]/ Н. Данфорд, Дж.Т. Шварц; под ред. А.Г. Костюченко; пер. с англ. Л.И. Головина, Б.С. Литягина. – М.: Издательство иностранной литературы, 1926.
[1] Ex и Ey - линейные многообразия, то есть если x, y Ex , то x + y Ey , при , .
Ex – область определения А;
Ey - область значения А;
[2] Равенства 1 и 2 определяются как аксиомы аддитивности и однородности;
[3]Шаром в метрическом пространстве называется совокупность элементов x пространства, удовлетворяющих условию p (xn, x0) < а.
Шар D(x0, a).
Если p (xn, x0) а, то D(x0, a) – замкнутый шар.
Если p (xn, x0) = а, то S(x0, a) – сфера.
Всякий шар метрического пространства, содержащий точку y, называется окрестностью точки y.
[4]Свойства нормы оператора.
1) Если оператор ограничен, , то и оператор ограничен, причем .
2) Если операторы ограничены, то и оператор ограничен, причем и .
[5]Линейный функционал, есть частный случай линейного оператора. Именно, линейный функционал есть линейный оператор, переводящий пространство E в числовую прямую.
[6] Резольвента – это функция комплексного переменного со значениями во множестве операторов, определенная на множестве регулярных чисел данного оператора.
Похожие работы
... понятия собственного числа линейного оператора А. 120. Определите, каким является базис а=(1/, 1/,1/), b=(1/, -1/, 0), с =(1/, 1/,-2/). Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЛИНЕЙНАЯ АЛГЕБРА Билет № 26 121. Приведение матрицы к ступенчатому виду методом Гаусса. Пример. 122. ...
... и1 и и2, соответствующие различным собственным значениям λ1 и λ2, ортогональны. Действительно, из соотношений Lu1 = λ1 и1, Lu2 = λ2и2, из вещественности λ1 и λ2 и из эрмитовости оператора L получаем цепочку равенств λ1(и1,и2) = (λ и1,и2) = (Lи1,и2) = (и1,Lu2) = (и1,λ2и2) = =λ2(и1,и2), т.е. λ1(и1,и2) = λ2(и1,и2). Отсюда, ...
... , называется оператором сдвига, если он каждую последовательность вида (х1,х2,…, хn…) переводит в последовательность вида (0, х1, х2, …, хn…), т.е. выполняется равенство: (х1,х2,…, хn…)=(0, х1, х2, …, хn…). Можно также рассматривать оператор сдвига, который действует в пространстве последовательностей, бесконечных в обе стороны. Элемент этого пространства можно представить в таком виде: (…х-2, ...
... состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при существует, но не непрерывна. Точечного спектра оператор не имеет. Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны ...
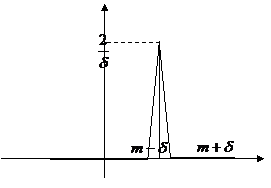

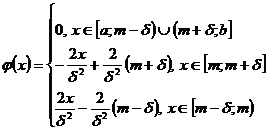

0 комментариев