В те времена, когда я преподавал математику в школе (1990-1997), столкнулся с проблемой отсутствия достаточного количества дидактических материалов на печатной основе для проведения занятий. В частности, при проведении контрольных работ было лишь два варианта заданий, и, естественно, ученики списывали, что, с моей точки зрения, недопустимо. Тогда я стал придумывать варианты заданий и распечатывать их с помощью старенькой пишущей машинки. Сразу замечу, что занятие это рутинное, абсолютно не творческое и скучное — придумать 20-25 однотипных вариантов с разным содержанием. Тем не менее, один год я такое практиковал.
Когда в институте меня стали учить программированию, тут же возникла идея приспособить для создания дидактических материалов компьютер. Он для этих целей идеально подходил, поскольку позволял автоматизировать не только распечатку текста, но и сам процесс его разработки. Действительно, достаточно запрограммировать образец для одного задания, и согласно ему будет получено любое количество заданий. Но и здесь были свои проблемы, связанные с тем, что сгенерированный текст DOS приходилось затем "доводить до ума" (ставить верхние и нижние индексы, рисовать дроби и т.д.) с помощью текстового редактора типа ChiWriter или Lexicon, причем конечный продукт выглядел в результате достаточно нелепо и коряво.
Технология окончательно сформировалась в 1994 г., когда я познакомился с системой форматирования текстов LaTeX, позволяющей форматировать тексты, содержащие математические формулы любой сложности. Обычно в основу самостоятельной или контрольной работы закладываются уже существующие дидактические материалы к тому или иному школьному учебнику математики, и по этому образу и подобию готовится работа, где данные в каждом из вариантов различные. Таким образом складывается иллюзия наличия такого же количества вариантов, сколько учеников в классе.
Наличие отдельного напечатанного варианта при проведении контрольной или самостоятельной работы имеет ряд преимуществ перед отсутствием такового: во-первых, решается проблема списывания — каждый учащийся вынужден обрабатывать свои данные (правда, при этом можно в качестве образца использовать работу соседа, но это было и при традиционном проведении контрольной работы); во-вторых, нет необходимости перед началом урока втискивать текст контрольной работы на доску (очень не люблю писать на доске!); в-третьих, ни для кого не является секретом, что зрение большинства учащихся в настоящее время ослаблено, и им приходится подходить к доске или переспрашивать учителя для уточнения текста задания, при указанном подходе проблема снимается. Можно найти и другие достоинства, мною не отмеченные, я думаю... Есть и свои недостатки — учителю затем нужно проверить не 2 варианта, а 25-30. Не всякий при нынешней загруженности на это решится. Но при желании число существенно разных вариантов можно сократить до 5-10.
Продемонстрирую на паре-тройке примеров технологию подготовки текста в формате LaTeX.
Пример 1. Алгебраическое выражение.
Одно из наиболее часто встречающихся в 5-7 классах заданий — вычисление значения выражения. Генерируя такие выражения, нужно учитывать такие обстоятельства, как:
1) соответствие изучаемой теме и возрасту учащихся (например, в 5 классе значение выражения не должно быть равно отрицательному числу);
2) после выполнения очередного действия полученное значение должно получиться проще и приемлемым для выполнения следующего действия, где это значение используется (т.е. некоторые величины в выражении будут случайными, другие — вычисляемыми);
3) при записи десятичной дроби в школьной математике используется десятичная запятая, а при записи на компьютере — десятичная точка;
4) если в записи выражения используются десятичные дроби, то они должны быть несократимыми и правильными.
Учитывая приведенные выше соображения, покажем на примере следующего числового выражения получение его аналогов:
![]()
Проанализируем данное выражение. Его значение равно 2,32 и получается как разность двух произведений. Таким образом, значение выражения — произвольное рациональное число, модуль которого не больше 10. Значение первого и второго произведений — десятичные дроби, это соответственно 2,62 и 0,3. При генерации произведений будем ориентироваться также на десятичные значения. В первом произведении первый сомножитель — сумма обыкновенных дробей с разными знаменателями, НОД которых отличен от 1, а второй сомножитель — число, которое можно сократить с общим знаменателем первого сомножителя. Второе произведение — произведение обыкновенной и десятичной дроби, которые нужно подобрать так, чтобы результат был точной десятичной дробью.
Приступим к генерации выражения. Пусть A=НОД(B,C), где B, C — знаменатели дробей суммы. Тогда B=A*B1, C=A*C1, где B1, C1 — случайные числа. D, F — числители рассматриваемых дробей, причем D<B, F<C. Целую часть первого слагаемого можно сгенерировать случайным образом. Второй сомножитель в первом произведении получаем так: K=НОК(B,C)*R/100, 1<R<10 — случайное число.
Аналогично получаем второй сомножитель. Не нужно забывать о том, что значение выражения по абсолютной величине не должно превышать 10.
Таким образом, выражение может быть получено с помощью следующего фрагмента программы:
B1 := 1 + Random(9);
C1 := 1 + Random(9);
A := 2 + Random(4); {НОД знаменателей дробей суммы}
B := A * B1; {Знаменатель первой дроби}
C := A * C1; {Знаменатель второй дроби}
D := 1 + Random(B — 2); {Числитель первой дроби}
F := 1 + Random(C — 2); {Числитель второй дроби}
K := Nod(D, B); {НОД чисел D, B}
D := D Div K; {Сокращение первой дроби}
B := B Div K;
K := Nod(F, C); {НОД чисел F, C}
F := F Div K; {Сокращение второй дроби}
C := C Div K;
K := B * C Div Nod(B, C) * (1 + Random(7)); {Второй сомножитель
в первом произведении}
Repeat
Repeat
M := 3 + Random(6); {Одно из чисел, на которое будет
производиться сокращение во втором произведении}
Ch1 := M * (1 + Random(3)) {Числитель второй дроби}
Until Odd(M) and Odd(Ch1);
Zn := M * 5; {Знаменатель первого сомножителя во втором
произведении}
SS := 2 + Random(4);
Zn1 := Stepen(2, SS); {Знаменатель второго сомножителя -
случайная степень числа 2}
Ch := Zn1 Div 2; {Числитель первой дроби}
Until (Ch < Zn) And (Ch1 < Zn1); {Повторяем генерацию дробей,
пока числители не станут
меньше знаменателей}
S := Nod(Ch, Zn);
Ch := Ch Div S; {Сокращение дроби}
Zn := Zn Div S;
Ch1 := Ch1 * Stepen(10, SS); {Подготовка числителя
второй дроби к целочисленному
делению}
{Печать результата генерации в файл Name}
WriteLn(Ch1, ' ', Zn1);
Write(Name, '$$left(', 1 + Random(3), 'frac{', D);
Write(Name, '}{', B, '}+frac{', F, '}{', C, '}right)cdot');
Write(Name, K Div 100, '{,}', K Mod 100, '-frac{', Ch);
WriteLn(Name, '}{', Zn, '}cdot 0{,}', Ch1 Div Zn1, '.$$')
В фрагменте программы использованы функции пользователя: Nod(A, B) — НОД(A,B); Stepen(A,B) — AB. Указанные функции должны быть описаны в программе.
Результаты работы программы для количества заданий, равного 5:
$$left(1frac{2}{3}+frac{5}{8}right)cdot0{,}48-frac{4}{35}cdot 0{,}875.$$
$$left(3frac{1}{2}+frac{1}{7}right)cdot0{,}98-frac{8}{35}cdot
0{,}4375.$$
$$left(2frac{10}{27}+frac{1}{18}right)cdot2{,}7-frac{8}{25}cdot
0{,}3125.$$
$$left(2frac{1}{2}+frac{5}{6}right)cdot0{,}24-frac{4}{15}cdot 0{,}375.$$
$$left(1frac{5}{6}+frac{3}{5}right)cdot1{,}5-frac{4}{35}cdot 0{,}875.$$
Результат обработки этого файла будет следующим:
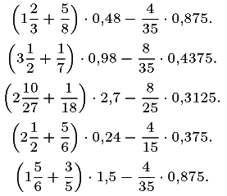
Пример 2. Квадратное уравнение.
Настоящий пример несколько проще предыдущего. Рассмотрим два случая: а) корни уравнения — целые; б) корни уравнения — обыкновенные дроби.
Как и в предыдущем случае, целесообразно идти к получению задания от ответа. Сгенерируем два корня уравнения и, используя теорему Виета, получим его коэффициенты. При генерации целых корней разумно сделать их различными и отличными от нуля. В приведенном ниже примере это задания по буквами а, б. При выводе задания в файл требуется учесть, что коэффициенты могут быть равны нулю, а также тот факт, что коэффициент, равный единице, не записывается.
Задания под в, г предполагают наличие двух различных корней, являющихся обыкновенными правильными дробями. Алгоритм получения соответствующих коэффициентов в этом случае более громоздкий, хотя в основу положена всё та же теорема Виета. Изначально опять же генерируем ненулевые различные корни уравнения, а затем на их основе получаем уравнение в целыми коэффициентами. В примере это делается поэтапно: сначала — корни уравнения; затем — коэффициенты уравнения — обыкновенные дроби, наконец, коэффициенты — целые числа, причем НОК(A, B, C) = 1.
Ниже приводятся законченный фрагмент программы , генерирующий задания, пример работы этой программы и результат обработки файла, полученного с помощью программы.
Program Kw;
Var F : Text;
{Процедура, производящая начальные установки в формате LaTeXа}
Procedure UST;
Begin
WriteLn(F, 'documentstyle[12pt,a4wide]{article}');
WriteLn(F, 'topmargin-3cm');
WriteLn(F, 'pagestyle{empty}');
WriteLn(F, 'setlength{textheight}{27cm}');
WriteLn(F, 'setlength{textwidth}{16cm}');
WriteLn(F, 'begin{document}');
END;
{НОД}
Function Nod (X, Y : Integer) : Integer;
Begin
WHILE X <> Y Do
IF X > Y THEN X := X — Y ELSE Y := Y — X;
Nod := X
END;
{НОК}
Function NoK (X, Y : Integer) : Integer;
Begin
NoK := X * Y Div NoD(X, Y)
END;
Var X1, I, X2, A, C, B : Integer;
Ch, Ch1, Zn, Zn1, BCh, BZn, CCh, CZn, J, V, Vsp : Integer;
Begin
Assign(F, 't:rustexkw_ur.tex');
ReWrite(F);
UST;
Randomize;
{Корни уравнения (целые)}
Repeat X1 := -10 + Random(21) Until X1 <> 0;
Repeat X2 := -10 + Random(21) Until X2 <> 0;
B := -(X1 + X2);
C := X1 * X2;
WriteLn(F, 'begin{tabular}{ll}');
Write(F, 'а)~$x^2');
If B <> 0
Then Begin
If B > 0
Then If B <> 1 Then Write(F, '+', B) Else Write(F, '+')
Else If B <> -1 Then Write(F, B) Else Write(F, '-');
Write(F, 'x');
End;
If C <> 0 Then If C < 0 Then Write(F, C) Else Write(F, '+', C);
WriteLn(F, '=0$;& б)~$');
Repeat X1 := -10 + Random(21) Until X1 <> 0;
Repeat X2 := -10 + Random(21) Until (X2 <> 0) And (X2 <> X1);
B := -(X1 + X2);
C := X1 * X2;
Write(F, 'x^2');
If B <> 0
Then Begin
If B > 0
Then If B <> 1 Then Write(F, '+', B) Else Write(F, '+')
Else If B <> -1 Then Write(F, B) Else Write(F, '-');
Write(F, 'x');
End;
If C <> 0 Then If C < 0 Then Write(F, C) Else Write(F, '+', C);
WriteLn(F, '=0$;');
{Генерируем уравнения с корнями — обыкновенными дробями}
For J := 0 To 1 Do
Begin
Repeat {первый корень}
Repeat Ch := -5 + Random(11) Until Ch <> 0; {числитель}
Zn := 2 + Random(8); {знаменатель}
V := Nod(Abs(Ch), Zn);
Ch := Ch Div V;
Zn := Zn Div V
Until (Zn > 1) And (Zn > Abs(Ch));
Repeat {второй корень}
Repeat Ch1 := -4 + Random(11) Until Ch1 <> 0;
Zn1 := 2 + Random(8);
V := Nod(Abs(Ch1), Zn1);
Ch1 := Ch1 Div V;
Zn1 := Zn1 Div V
Until (Zn1 > 1) And (Zn1 > Abs(Ch1)) And (Ch * Zn1 + Zn * Ch1 <> 0);
Vsp := Nod(Abs(Ch * Zn1 + Zn * Ch1), Zn1 * Zn);
BCh := (Ch * Zn1 + Zn * Ch1) Div Vsp; {числитель коэффициента B}
BZn := Zn * Zn1 Div Vsp; {знаменатель коэффициента B}
Vsp := Nod(Abs(Ch * Ch1), Zn1 * Zn);
CCh := Ch * Ch1 Div Vsp; {числитель коэффициента C}
CZn := Zn1 * Zn Div Vsp; {знаменатель коэффициента C}
A := Nok(BZn, CZn); {A}
B := BCh * A Div BZn; {B}
C := CCh * A Div CZn; {C}
Write(F, Chr(Ord('в') + J), ')~$', A, 'x^2');
If B <> 0
Then Begin
If B > 0
Then If B <> 1 Then Write(F, '+', B) Else Write(F, '+')
Else If B <> -1 Then Write(F, B) Else Write(F, '-');
Write(F, 'x');
End;
If C <> 0 Then If C < 0 Then Write(F, C) Else Write(F, '+', C);
Write(F, '=0$;');
If J = 0 Then WriteLn(F, '&') Else WriteLn(F, '');
End;
WriteLn(F, 'end{tabular}');
WriteLn(F);
WriteLn(F, 'end{document}');
Flush(F);
Close(F)
End.
documentstyle[12pt,a4wide]{article}
topmargin-3cm
pagestyle{empty}
setlength{textheight}{27cm}
setlength{textwidth}{16cm}
begin{document}
begin{tabular}{ll}
а)~$x^2+2x-8=0$;& б)~$
x^2-4x-45=0$;
в)~$49x^2-7x-6=0$;&
г)~$12x^2+16x+5=0$;
end{tabular}
end{document}
![]()
Если в приведенную выше программу внести незначительные изменения, то можно получить вариант , генерирующий логарифмические уравнения или какие-либо другие. Вот результат работы такой программы.
documentstyle[12pt,a4wide]{article}
topmargin-3cm
pagestyle{empty}
setlength{textheight}{27cm}
setlength{textwidth}{16cm}
begin{document}
begin{tabular}{ll}
а)~$log_{2}^2x-log_{2}x-20=0$;& б)~$log_{5}^2x
+7log_{5}x+10=0$;
в)~$15log_{3}^2x+22log_{3}x+8=0$;&
г)~$27log_{2}^2x+12log_{2}x+1=0$;
end{tabular}
end{document}
![]()
Пример 3. Задание по теме "Тождественные преобразования алгебраических выражений". (Из книги "Сборник задач для поступающих во втузы": Учеб. пособие / В.К. Егерев, Б.А. Кордемский, В.В. Зайцев и др.; Под. ред. М.И. Сканави. — 6-е изд., испр. и доп. — М.: "Столетие", 1997 — упр. 2.061, с. 21):
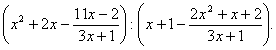
При решении поставленной задачи прежде всего проанализируем заданное выражение. Для этого выполним его преобразование и получим ответ:
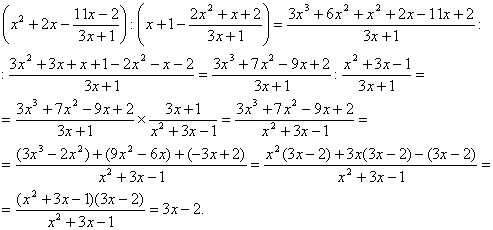
Таким образом, можно заметить, что числитель дроби-делимого, полученной после алгебраических преобразований в первых скобках, есть произведение ответа и числителя дроби-делителя, полученной после преобразований во вторых скобках. Следовательно, сам ответ, знаменатель дробей и числитель дроби-делителя могут быть сгенерированы произвольно, а на их основе строится дробь-делимое. Кроме того, для приведения выражения к виду, заданному в образце, необходимо и в первой, и во второй скобке числитель частично разделить на знаменатель.
Эти соображения и реализованы в приведенной ниже программе .
Program V;
Var F : Text;
{Процедура, производящая начальные установки в формате LaTeXа}
Procedure UST;
Begin
WriteLn(F, 'documentstyle[12pt,a4wide]{article}');
WriteLn(F, 'topmargin-3cm');
WriteLn(F, 'pagestyle{empty}');
WriteLn(F, 'setlength{textheight}{27cm}');
WriteLn(F, 'setlength{textwidth}{16cm}');
WriteLn(F, 'newcommand{ds}{displaystyle}');
WriteLn(F, 'begin{document}');
END;
Function Nod (X, Y : Integer) : Integer;
Begin
WHILE X <> Y Do
IF X > Y THEN X := X — Y ELSE Y := Y — X;
Nod := X
END;
Var D, I, A, C, B, E, G, H, O, P, L, M, N, E1, G1, H1, O1, P1 : Integer;
Vx2, J, Vsp : Integer;
X, Znak : Char;
Begin
Assign(F, 't:rustexex_v.tex');
ReWrite(F);
UST;
Randomize;
For I := 1 To 5 Do
Begin
Repeat {пока в числителях дробей не будут взаимно простые числа}
X := Chr(Ord('x') + Random(3)); {буква-переменная}
{Получаем знаменатель — выражение вида Ax+B,
A, B — целые, x — буква}
A := 1 + Random(5);
Repeat B := -4 + Random(9) Until B <> 0;
Vsp := Nod(A, Abs(B));
A := A Div Vsp; B := B Div Vsp;
Repeat
Repeat
{Получаем числитель делителя после преобразования
— выражение вида Lx^2+Mx+N,
L, M, N — целые, x — буква}
L := 1 + Random(5);
Repeat M := -4 + Random(9) Until M <> 0;
Repeat N := -4 + Random(9) Until N <> 0;
Vsp := Nod(Nod(L, Abs(M)), Abs(N));
L := L Div Vsp;
M := M Div Vsp;
N := N Div Vsp;
{Получаем ответ — выражение вида Cx+D,
C, D — целые, x — буква}
C := A * (1 + Random(3));
Repeat D := -4 + Random(9) Until D <> 0;
{Формируем выражение-делитель. Получаем его в виде
(Ex+G+(Hx^2+Ox+P)/(Ax+B))}
Repeat E := -3 + Random(7) Until E <> 0;
Repeat G := -3 + Random(7) Until G <> 0;
H := L — A * E;
O := M — (B * E + G * A);
P := N — B * G;
Until (H <> 0) And (O <> 0) And (P <> 0);
If H < 0 Then Begin Znak := '-'; H := -H; O := -O; P := -P End
Else Znak := '+';
{Формируем на основе ответа и делителя выражение-делимое
вида (E1x^2+G1x+(O1x+P1)/(Ax+B))}
E1 := C * L Div A;
Vx2 := D * L + M * C — E1 * B;
Until Vx2 Mod A = 0;
G1 := Vx2 Div A;
O1 := D * M + N * C — G1 * B;
P1 := D * N;
Until (Nod(Abs(H), Nod(Abs(O), Abs(P))) = 1) And (Nod(Abs(O1), Abs(P1)) = 1);
{выводим в файл очередное получившееся выражение,
учитывая, что некоторые из коэффициенты могут быть нулями,
коэффициенты, равные 1 или -1, не указываются и др.}
Write(F, Chr(Ord('а') + I — 1), ')~$dsleft(');
If Abs(E1) <> 1 Then Write(F, E1)
Else If E1 = -1 Then Write(F, '-');
Write(F, X, '^2');
If G1 <> 0
Then Begin
If Abs(G1) <> 1 Then Begin
If G1 > 0 Then Write(F, '+');
Write(F, G1)
End
Else If G1 = -1
Then Write(F, '-')
Else Write(F, '+');
Write(F, X);
End;
If O1 <> 0
Then Begin
If O1 < 0
Then Begin Write(F, '-'); O1 := -O1; P1 := -P1 End
Else Write(F, '+');
Write(F, 'frac{');
If O1 <> 1 Then Write(F, O1);
Write(F, X);
If P1 <> 0
Then Begin If P1 > 0 Then Write(F, '+');
Write(F, P1)
End;
Write(F, '}');
End
Else If P1 <> 0
Then Begin If P1 < 0
Then Write(F, '-')
Else Write(F, '+');
Write(F, 'frac{', Abs(P1), '}');
End;
If (O1 <> 0) Or (P1 <> 0)
Then Begin
Write(F, '{');
If A <> 1 Then Write(F, A);
Write(F, X);
If B > 0 Then Write(F, '+');
Write(F, B, '}')
End;
Write(F, 'right):left(');
If Abs(E) <> 1 Then Write(F, E)
Else If E = -1 Then Write(F, '-');
Write(F, X);
If G > 0 Then Write(F, '+');
Write(F, G);
Write(F, Znak, 'frac{');
If H <> 1 Then Write(F, H);
Write(F, X, '^2');
If O > 0 Then Write(F, '+');
If Abs(O) <> 1 Then Write(F, O)
Else If O = -1 Then Write(F, '-');
Write(F, X);
If P > 0 Then Write(F, '+');
Write(F, P, '}{');
If A <> 1 Then Write(F, A);
Write(F, X);
If B > 0 Then Write(F, '+');
WriteLn(F, B, '}right)$;');
WriteLn(F)
End;
WriteLn(F);
WriteLn(F, 'end{document}');
Flush(F);
Close(F)
End.
Вот один из результатов её работы:
documentstyle[12pt,a4wide]{article}
topmargin-3cm
pagestyle{empty}
setlength{textheight}{27cm}
setlength{textwidth}{16cm}
newcommand{ds}{displaystyle}
begin{document}
а)~$dsleft(6z^2+z+frac{13z+6}{3z-4}right):
left(-z-2+frac{5z^2-z-6}{3z-4}right)$;
б)~$dsleft(12y^2+20y+frac{19y-1}{y-1}right):
left(2y+3+frac{2y^2+3y+4}{y-1}right)$;
в)~$dsleft(4x^2-2x-frac{8x+3}{x+1}right):
left(-x-1+frac{3x^2+6x+2}{x+1}right)$;
г)~$dsleft(12x^2-22x+frac{39x+1}{x+2}right):
left(-2x+3+frac{6x^2+3x-7}{x+2}right)$;
д)~$dsleft(z^2+2z-frac{2z-9}{z-2}right):
left(-2z+2+frac{3z^2-9z+7}{z-2}right)$;
end{document}
А вот что получено после обработки этого документа с помощью LaTeX:
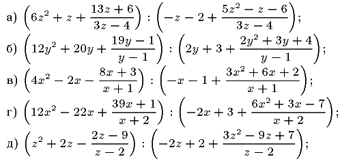
Итак, программа значительно увеличила количество заданий, отвечающих заданному образцу. Однако следует заметить, — в этот вариант программы не заложена гарантия, что все сгенерированные задания будут различны. Для подобного рода гарантий необходимо предпринять дополнительные уси
Похожие работы
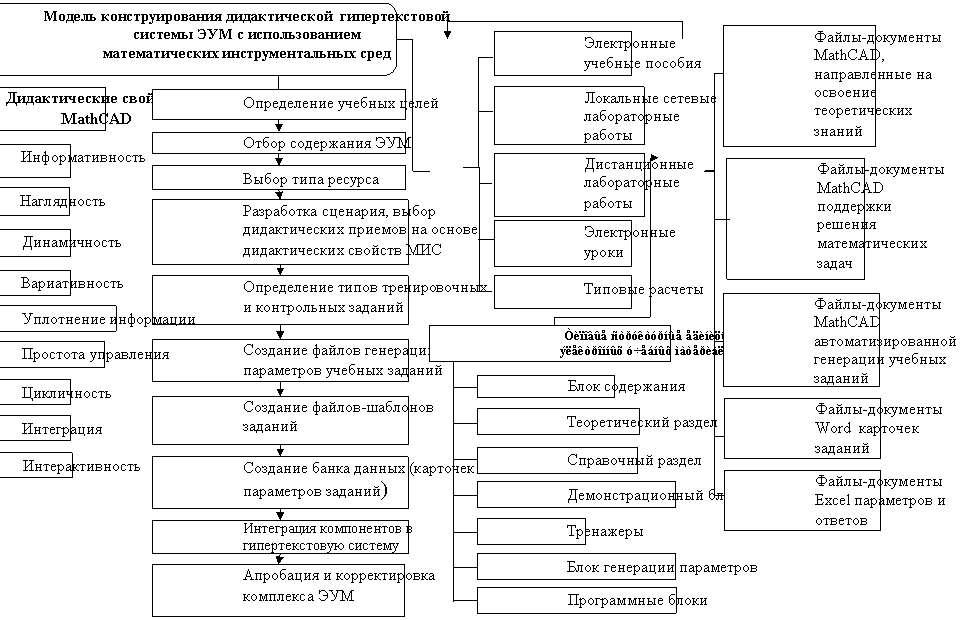
... системы электронных учебных материалов на основе технологии конструирования ЭУМ в среде MathCAD Происходит формирование умений и навыков конструирования электронных учебных материалов в среде MathCAD на творческом уровне В системе профессиональной подготовки учителей математики, физики, информатики недостаточно отражены подходы к созданию и применению электронных учебных материалов с ...
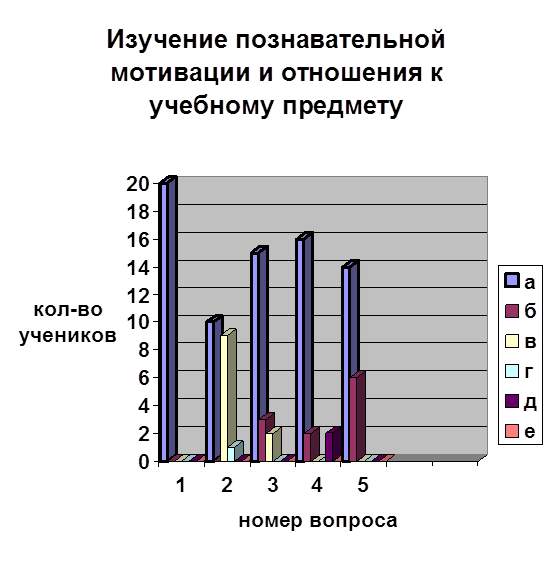
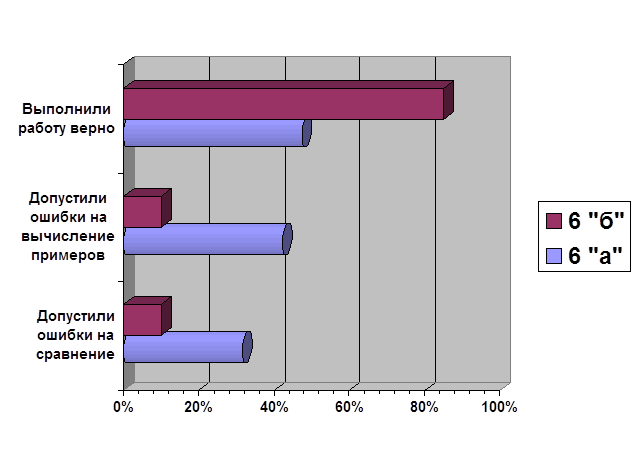
... дидактических игр на уроках математики, анализ игровой деятельности Изучив теоретические материалы по развитию мотивации познавательной деятельности, у автора возникло желание и интерес реализации этого на практике. Для того чтобы доказать или опровергнуть, что использование дидактических игр на уроках математики активизирует познавательную деятельность учащихся, автором работы в 6 «б» ...
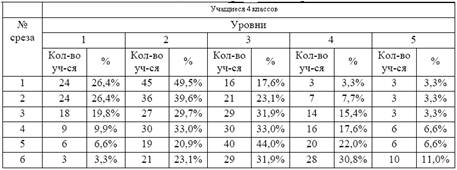
... 5 человек; низкий уровень мышления (6 баллов) – 4 человека. Далее переходим ко второму этапу эксперимента – формирующему. Описанию которого посвятим п.3.2. 3.2. ИСПОЛЬЗОВАНИЕ ПРОБЛЕМНЫХ СИТУАЦИЙ НА УРОКАХ МАТЕМАТИКИ В РАЗВИТИИ ТВОРЧЕСКОГО МЫШЛЕНИЯ УЧАЩИХСЯ В последнее время учителя начальных классов довольно часто при изучении математики создают на уроках проблемные ситуации. Однако чаще всего ...
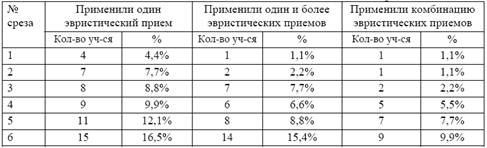
... в уровне развития от 4 до 38%, что подтверждает соответствующую часть гипотезы исследования. Таким образом, проведенное исследование доказало эффективность использования эвристической технологии в образовательном процессе школы. Заключение В результате нашего исследования нами было рассмотрено понятие "эвристическая технология", определены характерные особенности эвристической технологии в ...



0 комментариев