Навигация
Методы численного решения стационарного уравнения Шредингера
3. Методы численного решения стационарного уравнения Шредингера
3.1 Метод Нумерова
Рассмотрим решения одномерного стационарного уравнения Шредингера (3.1) частицы, движущейся в одномерном потенциале U(x).
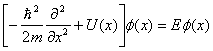 (3.1)
(3.1)
Будем при этом полагать, что его форма имеет потенциала, представленного на рис.1: в точках xmin, xmax потенциал становится бесконечно большим. Это означает, что в точках xmin, xmax расположены вертикальные стенки, а между ними находится яма конечной глубины.
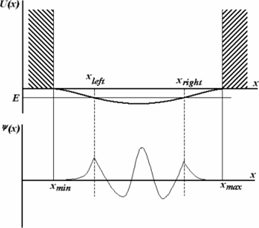
Рисунок 1.
Для удобства дальнейшего решения запишем уравнение Шредингера (3.1) в виде:
![]() (3.2)
(3.2)
Где
![]() (3.3)
(3.3)
С математической точки зрения задача состоит в отыскании собственных функций оператора![]() , отвечающим граничным условиям
, отвечающим граничным условиям
![]() (3.4)
(3.4)
и соответствующих собственных значений энергии E.
Так как ![]() при
при ![]() и
и ![]() при
при ![]() ,
, ![]() , то можно ожидать, что собственному решению данной задачи соответствует собственная функция, осциллирующая в классически разрешенной области движения
, то можно ожидать, что собственному решению данной задачи соответствует собственная функция, осциллирующая в классически разрешенной области движения ![]()
![]() и экспоненциально затухающим в запрещенных областях, где
и экспоненциально затухающим в запрещенных областях, где ![]()
![]() ,
,![]() , при
, при ![]() ,
, ![]()
![]() . Так как все состояния частицы в потенциальной яме оказываются связанными (т.е. локализованными в конечной области пространства), спектр энергий является дискретным. Частица, находящаяся в потенциальной яме конечных размеров
. Так как все состояния частицы в потенциальной яме оказываются связанными (т.е. локализованными в конечной области пространства), спектр энергий является дискретным. Частица, находящаяся в потенциальной яме конечных размеров ![]() при
при ![]() ,
, ![]() при
при ![]() , имеет дискретный спектр при
, имеет дискретный спектр при ![]() и непрерывный спектр при
и непрерывный спектр при ![]() .
.
Традиционно для решении задачи о нахождении собственных значений уравнения Шредингера используется метод пристрелки. Идея метода пристрелки состоит в следующем. Допустим, в качестве искомого значения ищется одно из связанных состояний, поэтому в качестве пробного начального значения энергии выбираем отрицательное собственное значение. Проинтегрируем уравнение Шредингера каким-либо известным численным методом на интервале ![]() . По ходу интегрирования от
. По ходу интегрирования от ![]() в сторону больших значений
в сторону больших значений ![]() сначала вычисляется решение
сначала вычисляется решение ![]() , экспоненциально нарастающее в пределах классически запрещенной области. После перехода через точку поворота
, экспоненциально нарастающее в пределах классически запрещенной области. После перехода через точку поворота ![]() , ограничивающую слева область движения разрешенную классической механикой, решение уравнения становится осциллирующим. Если продолжить интегрирование далее за правую точку поворота
, ограничивающую слева область движения разрешенную классической механикой, решение уравнения становится осциллирующим. Если продолжить интегрирование далее за правую точку поворота ![]() , то решение становится численно неустойчивым. Это обусловлено тем, что даже при точном выборе собственного значения, для которого выполняется условие
, то решение становится численно неустойчивым. Это обусловлено тем, что даже при точном выборе собственного значения, для которого выполняется условие ![]() , решение в области
, решение в области ![]() всегда может содержать некоторую примесь экспоненциально растущего решения, не имеющего физического содержания. Отмеченное обстоятельство является общим правилом: интегрирование по направлению вовнутрь области, запрещенной классической механикой, будет неточным. Следовательно, для каждого значения энергии более разумно вычислить еще одно решение
всегда может содержать некоторую примесь экспоненциально растущего решения, не имеющего физического содержания. Отмеченное обстоятельство является общим правилом: интегрирование по направлению вовнутрь области, запрещенной классической механикой, будет неточным. Следовательно, для каждого значения энергии более разумно вычислить еще одно решение ![]() , интегрируя уравнение (3.1) от
, интегрируя уравнение (3.1) от ![]() в сторону уменьшения
в сторону уменьшения ![]() . Критерием совпадения данного значения энергии является совпадение значений функций
. Критерием совпадения данного значения энергии является совпадение значений функций ![]() и
и ![]() в некоторой промежуточной точке
в некоторой промежуточной точке ![]() . Обычно в качестве данной точки выбирают левую точку поворота
. Обычно в качестве данной точки выбирают левую точку поворота ![]() . Так как функции
. Так как функции ![]() ,
,![]() являются решениями однородного уравнения (3.1), их всегда можно нормировать так, чтобы в точке
являются решениями однородного уравнения (3.1), их всегда можно нормировать так, чтобы в точке ![]() выполнялось условие
выполнялось условие ![]() . Помимо совпадения значений функций в точке
. Помимо совпадения значений функций в точке ![]() для обеспечения гладкости сшивки решений потребуем совпадения значений их производных
для обеспечения гладкости сшивки решений потребуем совпадения значений их производных ![]()
![]() (3.5)
(3.5)
Используя в (17) простейшие левую и правую конечно-разностные аппроксимации производных функций ![]() ,
, ![]() в точке
в точке ![]() , находим эквивалентное условие гладкости сшивки решений:
, находим эквивалентное условие гладкости сшивки решений:
![]() (3.6)
(3.6)
Число ![]() является масштабирующим множителем, который выбирается из условия
является масштабирующим множителем, который выбирается из условия ![]() Если точки поворота отсутствуют, т.е.
Если точки поворота отсутствуют, т.е. ![]() E>0, то в качестве
E>0, то в качестве ![]() можно выбрать любую точку отрезка
можно выбрать любую точку отрезка ![]() . Для потенциалов, имеющих более двух точек поворота и, соответственно, три или более однородных решений, общее решение получается сшивкой отдельных кусков. В описанном ниже документе, для интегрирования дифференциального уравнения второго порядка мы используем метод Нумерова. Для получения вычислительной схемы аппроксимируем вторую производную трехточечной разностной формулой:
. Для потенциалов, имеющих более двух точек поворота и, соответственно, три или более однородных решений, общее решение получается сшивкой отдельных кусков. В описанном ниже документе, для интегрирования дифференциального уравнения второго порядка мы используем метод Нумерова. Для получения вычислительной схемы аппроксимируем вторую производную трехточечной разностной формулой:
![]() (3.7)
(3.7)
Из уравнения (3.1) имеем
![]() (3.8)
(3.8)
Подставив (3.7) в (3.8) и перегруппировав члены, получаем
![]() (3.9)
(3.9)
Разрешив (3.9) относительно ![]() или
или ![]() , найдем рекуррентные формулы для интегрирования уравнения (3.1) вперед или назад по
, найдем рекуррентные формулы для интегрирования уравнения (3.1) вперед или назад по ![]() c локальной погрешностью
c локальной погрешностью ![]() . Отметим, что погрешность данного метода оказывается на порядок выше, чем погрешность метода Рунге-Кутта четвертого порядка. Кроме того данный алгоритм более эффективен, потому что значение функции
. Отметим, что погрешность данного метода оказывается на порядок выше, чем погрешность метода Рунге-Кутта четвертого порядка. Кроме того данный алгоритм более эффективен, потому что значение функции ![]() вычисляются только в узлах сетки. Для нахождения численного решения оказывается удобным провести обезразмеривание уравнения (3.1), используя в качестве единиц измерения расстояния
вычисляются только в узлах сетки. Для нахождения численного решения оказывается удобным провести обезразмеривание уравнения (3.1), используя в качестве единиц измерения расстояния ![]() - ширину потенциальной ямы, в качестве единиц измерения энергии - модуль минимального значения потенциала
- ширину потенциальной ямы, в качестве единиц измерения энергии - модуль минимального значения потенциала ![]() . В выбранных единицах измерения уравнение (3.1) имеет вид
. В выбранных единицах измерения уравнение (3.1) имеет вид
![]() (3.10)
(3.10)
где
![]()
![]()
![]()
![]() (3.11)
(3.11)
Таким образом, вычислительный алгоритм для нахождения собственных функций и собственных значений уравнения Шредингера реализуется следующей последовательностью действий:
1. Задать выражение, описывающее безразмерный потенциал ![]() .
.
2. Задать значение ![]() .
.
0 комментариев