Навигация
3. B-сплайны Шёнберга
В вычислительной математике B-сплайном называют сплайн-функцию, имеющую наименьший носитель для заданной степени, порядка гладкости и разбиения области определения. Фундаментальная теорема устанавливает, что любая сплайн-функция для заданной степени, гладкости и области определения может быть представлена как линейная комбинация B-сплайнов той же степени и гладкости на той же области определения. [1] Термин B-сплайн был введён И. Шёнбергом и является сокращением от словосочетания «базисный сплайн». [2] B-сплайны могут быть вычислены с помощью алгоритма де Бора, обладающего устойчивостью.
В системах автоматизированного проектирования и компьютерной графике термин B-сплайн часто описывает сплайн-кривую, которая задана сплайн-функциями, выраженными линейными комбинациями B-сплайнов.
Когда узлы равноудалены друг от друга, говорят, что B-сплайн является однородным, в противном случае его называют неоднородным.
Когда количество узлов совпадает со степенью сплайна, B-сплайн вырождается в кривую Безье. Форма базисной функции определяется расположением узлов. Масштабирование или параллельный перенос базисного вектора не влияет на базисную функцию.
Сплайн содержится в выпуклой оболочке его опорных точек.
Базисный сплайн степени n: ![]() .
.
не обращается в нуль только на промежутке [ti, ti+n+1], то есть:
![]() . (3.1)
. (3.1)
Другими словами, изменение одной опорной точки влияет только на локальное поведение кривой, а не на глобальное, как в случае кривых Безье.
Базисная функция может быть получена из полинома Бернштейна
В-сплайн и некоторые наиболее часто используемые базисыТеорема Стренга-Фикса указывает на то, что если стандартную финитную функцию ![]() выбрать исходя из условия (2.7), то ряд (2.4), построенный на основе ее сдвигов, будет обладать хорошими аппроксимационными свойствами.
выбрать исходя из условия (2.7), то ряд (2.4), построенный на основе ее сдвигов, будет обладать хорошими аппроксимационными свойствами.
Шенберг предложил один интересный класс функций, удовлетворяющих условию (2.7). Функцию ![]() называют В-сплайном (Шенберга) степени
называют В-сплайном (Шенберга) степени ![]() , если ее преобразование Фурье имеет вид
, если ее преобразование Фурье имеет вид
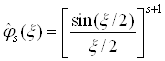 . (3.2)
. (3.2)
Как видим, функция (6.8) удовлетворяет всем условиям (6.7).
Базис из ступенек
Довольно просто показать, что при ![]()
|
 (3.3)
(3.3)
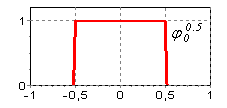
В этом случае базис представляет собой набор сдвигов (2.5) стандартной ступеньки ![]() (3.3), а функция
(3.3), а функция ![]() представляет собой разрывную ступенчатую функцию (
представляет собой разрывную ступенчатую функцию (![]() ). Аппроксимация по норме
). Аппроксимация по норме ![]() имеет порядок
имеет порядок ![]() . Такой базис может быть выбран в качестве второго базиса
. Такой базис может быть выбран в качестве второго базиса ![]() при использовании метода Галеркина-Петрова.
при использовании метода Галеркина-Петрова.
Базис из крышек
Рассмотрим В-сплайн степени ![]() :
: 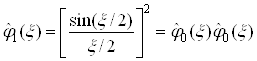 . Из этого соотношения следует, что
. Из этого соотношения следует, что ![]() получается как свертка функций
получается как свертка функций ![]() =
= 
После несложных преобразований получаем:
|
 (3.4)
(3.4)
Функция ![]() представляет собой аппроксимацию непрерывной ломаной линией, имеющей разрывные производные. Аппроксимация по норме
представляет собой аппроксимацию непрерывной ломаной линией, имеющей разрывные производные. Аппроксимация по норме ![]() имеет второй порядок, по норме
имеет второй порядок, по норме ![]() – первый. Эта аппроксимация используется наиболее часто при решении дифференциальных уравнений второго порядка проекционным методом. Она приводит к наиболее простым формулам для интегралов и максимально разреженной матрице при ее вычислении.
– первый. Эта аппроксимация используется наиболее часто при решении дифференциальных уравнений второго порядка проекционным методом. Она приводит к наиболее простым формулам для интегралов и максимально разреженной матрице при ее вычислении.
Кроме того, у этого базиса, ввиду того, что p=1, есть одна особенность – для аппроксимируемой функции ![]() значения коэффициентов
значения коэффициентов ![]() совпадают со значениями функции в узлах сетки
совпадают со значениями функции в узлах сетки ![]() , что позволяет быстро находить начальные приближения для
, что позволяет быстро находить начальные приближения для ![]() .
.
В-сплайн степени ![]() представляет собой кусочно-полиноминальный кубический сплайн, который получается сверткой:
представляет собой кусочно-полиноминальный кубический сплайн, который получается сверткой:
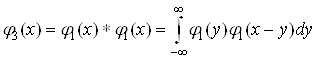 .
.
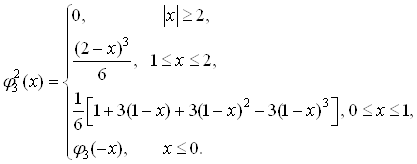 (3.5)
(3.5)

Размер носителя при ![]() увеличился до четырех (
увеличился до четырех (![]() ). Заметим, что для обеспечения непрерывности второй производной в точках
). Заметим, что для обеспечения непрерывности второй производной в точках ![]() выполняется условие
выполняется условие ![]() . Как уже отмечалось, аппроксимация по норме
. Как уже отмечалось, аппроксимация по норме ![]() имеет четвертый порядок, по норме
имеет четвертый порядок, по норме ![]() – третий.
– третий.
Литература
1. Роджерс Д., Адамс Дж. Математические основы машинной графики. – М.: Мир, 2001.
2. Корнейчук, Н.П., Бабенко, В.Ф., Лигун, А.А. Экстремальные свойства полиномов и сплайнов / отв. ред. А.И. Степанец; ред. С.Д. Кошис, О.Д. Мельник, АН Украины, Ин-т математики.–К.: Наукова думка, 1992.–304 с.
3. Роджерс Д., Адамс Дж. Математические основы машинной графики. – М.: Мир, 2001.
4. Лившиц Евгений Давидович. Непрерывные E-выборки для приближения полиномиальными и рациональными сплайнами: Дис. … канд. физ.-мат. наук: 01.01.01 Москва, 2005 90 с.
5. Алберг Дж., Нильсон Э., Уолш Дж. – Теория сплайнов и ее приложения
6. Винниченко Л.Ф. Экспоненциальные гистосплайны: предпосылки введения // Publishing house Education and Science s.r.o., конференция «Европейская наука XXI века», 2009
7. Корнейчук, Н.П., Бабенко, В.Ф., Лигун, А.А. Экстремальные свойства полиномов и сплайнов / отв. ред. А.И. Степанец; ред. С.Д. Кошис, О.Д. Мельник, АН Украины, Ин-т математики. – К.: Наукова думка, 1992.–304 с.
Похожие работы
... в и представление (4) единственно. Эта формула называется представлением сплайна в виде суммы усеченных степенных функций. Итак, множество является конечномерным пространством размерности §2. Базисные сплайны с конечными носителями В математическом анализе встречаются конструкции, связанные с финитными функциями, т. е. гладкими функциями, которые определяются на всей действительной оси, ...
... часть пульта управления (или устройства вывода данных) оператора-рентгенолога. Аналогичные пульты управления можно применять и в других системах получения изображения, например на основе ядерного магнитного резонанса или компьютерной томографии. Цифровое изображение можно записать на магнитном носителе, оптическом диске или же на специальном записывающем устройстве, способном постоянно вести ...



0 комментариев