Навигация
Случай: x = (4k-1)/2, kÎZ
1 случай: x = (4k-1)/2, kÎZ
Тогда ![]() , так как
, так как ![]() - целое число.
- целое число.
Получим ![]() =
=![]() =
=![]() =
=![]() =
=![]()
2 случай: x ¹ (4k-1)/2, k Î Z, тогда ![]() .
.
Получим ![]() =
=![]() =
=![]()
Итак, данное выражение округляет числа до ближайшего целого; в случае «равновесия» — когда x лежит ровно посередине между целыми числами — данное выражение округляет число в сторону чётного.
Задача 9.
Докажите, что ![]() при любом целом n и любом целом положительном m.
при любом целом n и любом целом положительном m.
Доказательство:
Пусть 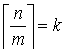 .
.
Покажем, что  .
.
Имеем 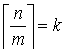 Û
Û
Û ![]() (по свойствам (4)) Û
(по свойствам (4)) Û
Û ![]() Û
Û
Û ![]() Û
Û
Û ![]() Û
Û
Û ![]() Û
Û
Û 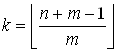
Что и требовалось доказать.
Задача 10.
Пусть α и β — вещественные положительные числа. Докажите, что Spec(α) и Spec(β) образуют разбиение всех целых положительных чисел тогда и только тогда, когда α и β иррациональны и  .
.
Решение:
Пусть α и β — вещественные положительные числа.
Докажем, что если Spec(α) и Spec(β) образуют разбиение всех целых положительных чисел, то α и β — иррациональные числа и  .
.
Spec(α) и Spec(β) образуют разбиение всех целых положительных чисел, тогда ![]() .
.
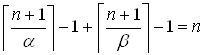 Þ
Þ
Þ 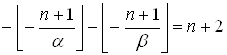 Þ
Þ
Þ  Þ
Þ
Þ  Þ
Þ
Þ ![]()

Рассмотрим  Þ
Þ
Þ  .
.
Докажем, что α и β иррациональны. Так как  , то числа α и β либо оба рациональны, либо оба иррациональны.
, то числа α и β либо оба рациональны, либо оба иррациональны.
Если α и β оба рациональны, т.е. существует такое целое число m, что 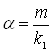 и
и  , где
, где ![]() и
и ![]() — натуральные числа, тогда
— натуральные числа, тогда ![]() ÎSpec(α) и
ÎSpec(α) и ![]() ÎSpec(β).
ÎSpec(β).
Но никакое число не содержится одновременно в двух спектрах, образующих разбиение всех целых положительных чисел. Следовательно, α и β — иррациональны.
Докажем обратное: если α и β иррациональны и  , то Spec(α) и Spec(β) образуют разбиение всех целых положительных чисел.
, то Spec(α) и Spec(β) образуют разбиение всех целых положительных чисел.
 Þ
Þ 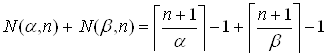
Так как ![]() и
и ![]() — иррациональны, то
— иррациональны, то ![]() и
и ![]() — не целые числа, то
— не целые числа, то

и

Отсюда получаем:
![]()
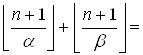
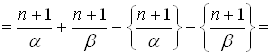
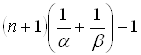 (так как
(так как  и
и ![]() и
и ![]() — иррациональны, то
— иррациональны, то 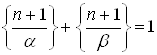 ).
).
Получаем, что![]() . Отсюда Spec(α) и Spec(β) образуют разбиение всех натуральных чисел.
. Отсюда Spec(α) и Spec(β) образуют разбиение всех натуральных чисел.
Что и требовалось доказать.
Задача 11.
Докажите, что ![]() при целом n.
при целом n.
Доказательство:
· если ![]() (
(![]() или
или ![]() ), то
), то ![]() ,
,
тогда ![]() .
.
Получаем верное равенство ![]() .
.
· если ![]() , тогда
, тогда ![]() .
.
Правая часть имеет вид: 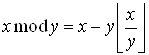 .
.
Преобразуем левую часть:
![]()
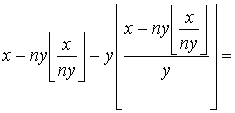
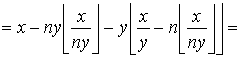

 .
.
Получили, что ![]() при любом целом
при любом целом ![]() . Что и требовалось доказать.
. Что и требовалось доказать.
Задача 12.
Имеется ли аналогичное (16) тождество, в котором вместо «полов» используются «потолки»?
Решение:
Тождество (16) ![]() получается из тождества (15)
получается из тождества (15)  заменой n на ëmxû.
заменой n на ëmxû.
Аналогичное тождество для потолков получается из тождества (14) ![]() заменой n на émxù:
заменой n на émxù:
émxù =![]() =
=
=![]() =
=![]()
Итак, получили тождество аналогичное данному:
![]() émxù =
émxù =![]() .
.
Задача 13.
Докажите, что ![]() . Найдите и докажите аналогичное выражение для
. Найдите и докажите аналогичное выражение для ![]() вида
вида ![]() , где ω – комплексное число
, где ω – комплексное число ![]() .
.
Доказательство:
При делении числа на 2 возможны только два различных остатка: либо 0, либо 1.
· если ![]() , то
, то ![]() и
и ![]() .
.
· если ![]() ,
, ![]() и
и ![]() .
.
Следовательно, равенство ![]() верно для любого натурального n. Что и требовалось доказать.
верно для любого натурального n. Что и требовалось доказать.
Найдём аналогичное выражение для ![]() , т.е. найдём коэффициенты a, b, c.
, т.е. найдём коэффициенты a, b, c.
Поскольку ![]() — есть корень третьей степени из 1, то
— есть корень третьей степени из 1, то ![]() и
и ![]() .
.
Так как ![]() , то
, то ![]() .
.
При делении числа на 3 возможны только три различных остатка: либо 0, либо 1, либо 2.
Если ![]() , то
, то ![]() .
.
Если ![]() , то
, то ![]() .
.
Если ![]() , то
, то ![]() .
.
Решая систему  , находим a, b, c.
, находим a, b, c.
![]() ,
, ![]() ,
, ![]() .
.
Итак, получаем следующую формулу:
![]() .
.
Задача 14.
Какому необходимому и достаточному условию должно удовлетворять вещественное число ![]() , чтобы равенство
, чтобы равенство ![]() выполнялось при любом вещественном
выполнялось при любом вещественном ![]() ?
?
Решение:
При любом вещественном ![]() и
и ![]() равенство
равенство ![]() выполняется Û b — целое число.
выполняется Û b — целое число.
Если b — целое число, то функция ![]() непрерывная, возрастающая функция (так как
непрерывная, возрастающая функция (так как ![]() ). Пусть
). Пусть ![]() — целое число, т.е.
— целое число, т.е. ![]() . Тогда
. Тогда ![]() , так как
, так как ![]() и
и ![]() . Выражая
. Выражая ![]() через
через ![]() , получим
, получим ![]() — целое, как натуральное число в неотрицательной целой степени. Поэтому можно применить формулу (6) и получить равенство
— целое, как натуральное число в неотрицательной целой степени. Поэтому можно применить формулу (6) и получить равенство ![]() .
.
Если b — не целое число, то при ![]() равенство
равенство ![]() не будет выполняться, так как
не будет выполняться, так как ![]()
Итак, если ![]() , то равенство
, то равенство ![]() выполняется при любом вещественном
выполняется при любом вещественном ![]() тогда и только тогда, когда b — целое число.
тогда и только тогда, когда b — целое число.
Ответ: b — целое число.
Задача 15.
Найдите сумму всех чисел, кратных x, в замкнутом интервале [a, b], при ![]() .
.
Решение:
Числа, кратные ![]() имеют вид
имеют вид ![]() , где
, где ![]() . Нужно просуммировать те из чисел
. Нужно просуммировать те из чисел ![]() , для которых
, для которых ![]() . Учитывая, что
. Учитывая, что ![]() и (4), имеем
и (4), имеем
![]() Û
Û ![]() Û
Û  .
.
Нам нужно вычислить следующую сумму:
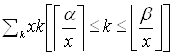 .
.
В этой сумме ![]() можно вынести за скобки, а в скобке останется сумма всех чисел от
можно вынести за скобки, а в скобке останется сумма всех чисел от ![]() до
до ![]() включительно. Применяя формулу арифметической прогрессии получаем:
включительно. Применяя формулу арифметической прогрессии получаем:
 .
.
Задача 16.
Покажите, что n-й член последовательности 1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,… равен![]() . (Каждое число m входит в данную последовательность m раз.)
. (Каждое число m входит в данную последовательность m раз.)
Решение:
В этой последовательности чисел меньших ![]() будет
будет ![]() , а чисел не превосходящих
, а чисел не превосходящих ![]() будет
будет ![]() . Поэтому, если xn=m, то
. Поэтому, если xn=m, то
Оценим n:
![]() Û
Û
Û ![]() Û
Û
Û ![]() Û
Û
Û ![]() Û
Û
Û 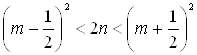 Û
Û
Û ![]() Û
Û
Û ![]() Þ
Þ
Þ 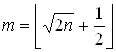 .
.
Следовательно,  .
.
Задача 17.
Найдите и докажите связь между мультимножествами Spec(α) и Spec(α/(α+1)), где α — некоторое положительное вещественное число.
Решение:
Число элементов в Spec(α), которые не превосходят n:
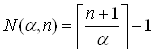 .
.
Число элементов в Spec(α/(α+1)), которые не превосходят n:
 .
.
Итак, получили, что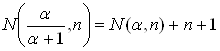 .
.
Покажем на основе этого, что чисел равных ![]() в Spec
в Spec будет на 1 больше, чем в Spec(
будет на 1 больше, чем в Spec(![]() ).
).
При ![]() если
если ![]() , тогда
, тогда 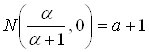 .
.
Пусть в Spec(![]() ) элементов не превосходящих
) элементов не превосходящих ![]() будет
будет ![]() , тогда число элементов в Spec(
, тогда число элементов в Spec(![]() ) равных
) равных ![]() будет
будет ![]() . Подсчитаем количество элементов в Spec
. Подсчитаем количество элементов в Spec равных
равных ![]() :
:

Что и требовалось доказать.
Ответ: чисел равных ![]() в Spec
в Spec будет на 1 больше, чем в Spec(
будет на 1 больше, чем в Spec(![]() ).
).
Задача 18.
На шахматной доске ![]() клеток симметрично начерчена окружность с диаметром
клеток симметрично начерчена окружность с диаметром ![]() единиц. Через сколько клеток доски проходит данная окружность?
единиц. Через сколько клеток доски проходит данная окружность?
Решение:
Радиус окружности равен 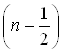 .
.
Горизонтальных прямых, не являющихся сторонами квадрата — (![]() ).
).
Вертикальных прямых, не являющихся сторонами квадрата — (![]() ).
).
Окружность каждую из указанных прямых пересекает в двух точках. Она не проходит через углы клеток. Действительно, если предположить, что данная окружность проходит через какой-нибудь угол клетки, то существуют такие целые числа ![]() и
и ![]() , для которых выполняется теорема Пифагора:
, для которых выполняется теорема Пифагора:  , но
, но ![]() — целое число, а
— целое число, а 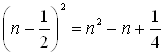 — не целое. Получили противоречие. Следовательно, окружность не проходит через углы клеток.
— не целое. Получили противоречие. Следовательно, окружность не проходит через углы клеток.
Каждую клетку окружность пересекает в двух точках, а каждая точка пересечения принадлежит двум клеткам. Следовательно, окружность проходит через столько клеток доски, сколько имеется точек пересечения её с прямыми: ![]() .
.
Ответ: ![]() клеток.
клеток.
Задача 19.
Говорят, что f(x) является репликативной функцией, если
f(![]() ) = f(
) = f(![]() ) + f
) + f  + … + f
+ … + f 
при каждом целом положительном m. Укажите, какому необходимому и достаточному условию должно удовлетворять вещественное число c, чтобы функция f(x) = x+c являлась репликативной.
Решение:
f(x) = x+c — репликативна Û
Û 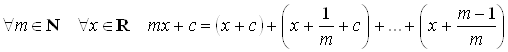 Û
Û
Û ![]() Û
Û
Û 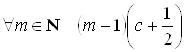 = 0 Û
= 0 Û ![]() .
.
Ответ: ![]() .
.
Р.Грэхем, Д.Кнут, О.Паташник. Конкретная математика. М.: «Мир» 1998. С 88 - 124.
Похожие работы
... программе. В данном разделе они перечислены в алфавитном порядке и приводятся с объяснениями. Эти ошибки могут являться следствием случайного затирание памяти программой. Abnormal program termination Аварийное завершение программы Данное сообщение может появляться, если для выполнения программы не может быть выделено достаточного количества памяти. Более подробно оно рассматривается в конце ...
... дискретного программирование для решения задач проектирование систем обработки данных. - Сформулированы задачи диссертационного исследования. 2. БЛОЧНО-СИММЕТРИЧНЫЕ МОДЕЛИ И МЕТОДЫ ПРОЕКТИРОВАНИЯ СИСТЕМ ОБРАБОТКИ ДАННЫХ В данном разделе рассматриваются общая постановка блочно-симметричной задачи дискретного программирования, её особенности и свойства. Разработан общий подход решения задач ...
... - число пи. 11. Sin(x) - синус. 12. Cos(x) - косинус. 13. Arctan(x) - арктангенс. Все остальные математические функции можно получить, пользуясь этим основным набором; например: десятичный логарифм - Ln(x)/Ln(10), тангенс - Sin(x)/Cos(x) и т.д. Аргументы функций могут быть любыми арифметическими выражениями и задаются в круглых скобках после имени функции, аргументы функций Sin и Cos выражаются в ...
... вычисления значений этой функции на интервале аппроксимации. Приведение аргумента к интервалу аппроксимации является обязательным этапом как при использовании итеративных методов вычисления элементарных функций, так и при многочленной и рациональной аппроксимации. Этот прием позволяет сократить число операций необходимых для вычисления значения элементарной функции за счет уменьшения количества ...



0 комментариев