Навигация
Метод ортогоналізації у випадку несиметричної матриці
1.2 Метод ортогоналізації у випадку несиметричної матриці
У випадку несиметричної матриці процес ортогоналізації проводиться точно також. Нехай вектори ![]() вже побудовані. Тоді
вже побудовані. Тоді ![]() шукається у вигляді
шукається у вигляді
![]() (29)
(29)
Коефіцієнти ![]() визначаються із системи
визначаються із системи
![]() (30)
(30)
Система у випадку несиметричної матриці буде трикутною.
Аналогічно будується система «біортогональних» векторів, тобто система 2n векторів, що задовольняють умові (12). При цьому ![]() – n довільних лінійно незалежних векторів, а вектори
– n довільних лінійно незалежних векторів, а вектори ![]() будуються послідовно у вигляді
будуються послідовно у вигляді
![]() (31)
(31)
Коефіцієнти ![]() перебувають із системи
перебувають із системи
![]() (32)
(32)
Також надходимо, відшукуючи коефіцієнти ![]() й
й ![]() , при побудові систем векторів (14) і (15), що задовольняють умовам (16).
, при побудові систем векторів (14) і (15), що задовольняють умовам (16).
При цьому одержимо дві системи:
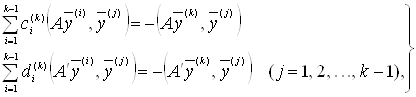 (33)
(33)
з яких і визначаємо ![]() й
й ![]() .
.
Зупинимося ще на одному методі ортогоналізації. Будемо розглядати рядки матриці А як вектори:
![]() (34)
(34)
Перше рівняння системи ![]() ділимо на
ділимо на 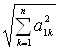 . При цьому одержимо
. При цьому одержимо
![]() (35)
(35)
де
 (36)
(36)
Друге рівняння системи заміниться на
![]() (37)
(37)
де
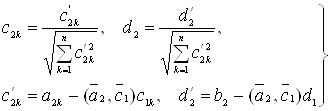 (38)
(38)
Аналогічно надходимо далі. Рівняння з номером i прийме вид
![]() (39)
(39)
де

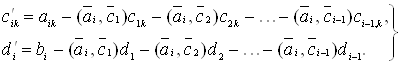 (40)
(40)
Процес буде здійсненний, якщо система рівнянь лінійно незалежна. У результаті ми прийдемо до нової системи ![]() , де матриця З буде ортогональної, тобто має властивість СС¢=I.
, де матриця З буде ортогональної, тобто має властивість СС¢=I.
Таким чином, рішення системи можна записати у вигляді
![]() . (41)
. (41)
Практично, внаслідок помилок округлення, СС¢ буде відмінна від одиничної матриці й може виявитися доцільним зробити кілька ітерацій для системи ![]() .
.
2. Метод сполучених градієнтів
2.1 Перший алгоритм методу
Нехай потрібно вирішити систему лінійних алгебраїчних рівнянь
![]() (1)
(1)
с позитивно певною матрицею A порядку n.
Розглянемо функціонала
![]() , (2)
, (2)
багаточлен, що представляє, другого порядку відносно x1, x2…, xn,… Позначимо через ![]() рішення системи (1), тобто
рішення системи (1), тобто ![]() . У силу симетричності й позитивної визначеності матриці, маємо:
. У силу симетричності й позитивної визначеності матриці, маємо:

При цьому знак рівності можливий лише при ![]() . Таким чином, задача рішення рівняння (1) зводиться до задачі відшукання вектора
. Таким чином, задача рішення рівняння (1) зводиться до задачі відшукання вектора ![]() , що обертає в мінімум функціонал (2).
, що обертає в мінімум функціонал (2).
Для відшукання такого вектора застосуємо наступний метод.
Нехай ![]() – довільний початковий вектор, а
– довільний початковий вектор, а
![]() (4)
(4)
– вектор не в'язань системи. Покажемо, що вектор не в'язань ![]() має напрямок нормалі до поверхні
має напрямок нормалі до поверхні ![]() в крапці
в крапці ![]() . Справді, напрямок нормалі збігається з напрямком найшвидшої зміни функції
. Справді, напрямок нормалі збігається з напрямком найшвидшої зміни функції ![]() в крапці
в крапці ![]() . Це напрямок ми знайдемо, якщо знайдемо серед векторів
. Це напрямок ми знайдемо, якщо знайдемо серед векторів ![]() , для яких
, для яких ![]() , такий вектор, що
, такий вектор, що

має найбільше значення. Але

Але серед векторів ![]() постійний довжини
постійний довжини ![]() досягає максимального значення, якщо
досягає максимального значення, якщо ![]() має напрямок вектора
має напрямок вектора ![]() або йому протилежне. Твердження доведене. Будемо рухатися із крапки
або йому протилежне. Твердження доведене. Будемо рухатися із крапки ![]() в напрямку вектора
в напрямку вектора ![]() доти, поки функція
доти, поки функція ![]() досягає мінімального значення. Це буде при
досягає мінімального значення. Це буде при ![]() , тобто при
, тобто при
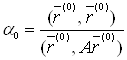 . (5)
. (5)
Вектор
![]() (6)
(6)
і приймаємо за нове наближення до рішення.
У методі сполучених градієнтів наступне наближення ![]() перебуває так. Через крапку
перебуває так. Через крапку ![]() проведемо гіперплощину (n-1) – го виміру
проведемо гіперплощину (n-1) – го виміру
![]() (7)
(7)
і через ![]() позначимо нове не в'язання системи
позначимо нове не в'язання системи
![]() . (8)
. (8)
Вектор ![]() спрямований по нормалі до поверхні
спрямований по нормалі до поверхні ![]() в крапці
в крапці ![]() , а вектор
, а вектор ![]() паралельний дотичної площини в цій крапці. Тому
паралельний дотичної площини в цій крапці. Тому
![]() . (9)
. (9)
Гіперплощина (7) проходить через крапку ![]() , тому що
, тому що
![]() .
.
При кожному ![]() вектор
вектор ![]() паралельний деякої нормальної площини до поверхні
паралельний деякої нормальної площини до поверхні ![]() в крапці
в крапці ![]() . Знайдемо серед них той, котрий лежить у гіперплощині (7), тобто ортогональний к.
. Знайдемо серед них той, котрий лежить у гіперплощині (7), тобто ортогональний к.![]() З умови ортогональності маємо:
З умови ортогональності маємо:
![]() ,
,
або
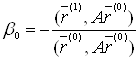 . (10)
. (10)
Вектор
![]() (11)
(11)
має напрямок нормалі до перетину поверхні ![]() гіперплощини (7) у крапці
гіперплощини (7) у крапці ![]() . Будемо рухатися із крапки
. Будемо рухатися із крапки ![]() в напрямку вектора
в напрямку вектора ![]() доти, поки функція
доти, поки функція ![]() досягне мінімуму. Це буде при
досягне мінімуму. Це буде при
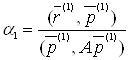 . (12)
. (12)
Вектор
![]()
приймемо за нове наближення до рішення ![]() системи. Вектор не в'язань
системи. Вектор не в'язань
![]() (13)
(13)
має напрямок нормалі до поверхні ![]() в крапці
в крапці ![]() . Покажемо, що він буде ортогональний до
. Покажемо, що він буде ортогональний до ![]() і
і ![]() . Справді, використовуючи (9), (11), (12), (13), маємо:
. Справді, використовуючи (9), (11), (12), (13), маємо:

Розглянемо гіперплощину (n-2) – х вимірів
![]() , (14)
, (14)
минаючу через крапку ![]() . Ця гіперплощина містить і
. Ця гіперплощина містить і ![]() , тому що ми раніше бачили, що
, тому що ми раніше бачили, що ![]() , а
, а
![]() .
.
Вектор ![]() при кожному
при кожному ![]() паралельний гіперплощини (7), тому що
паралельний гіперплощини (7), тому що
 .
.
Підберемо ![]() так, щоб він був паралельний і гіперплощини (14), тобто зажадаємо ортогональності до вектора
так, щоб він був паралельний і гіперплощини (14), тобто зажадаємо ортогональності до вектора ![]() . Будемо мати:
. Будемо мати:
![]() ,
,
або
 (15)
(15)
Вектор
![]() (16)
(16)
буде мати напрямок нормалі до перетину поверхні ![]() гіперплощиною (14) у крапці
гіперплощиною (14) у крапці ![]() . Із крапки
. Із крапки ![]() змістимося в напрямку цього вектора так, щоб функція
змістимося в напрямку цього вектора так, щоб функція ![]() досягла мінімального значення. Це буде при
досягла мінімального значення. Це буде при
 , (17)
, (17)
![]() (18)
(18)
приймемо за нове наближення к.![]() Новий вектор не в'язань буде:
Новий вектор не в'язань буде:
![]() . (19)
. (19)
Продовжуючи процес, одержимо послідовності векторів ![]() ,
, ![]() ,
, ![]() , обумовлені рекурентними співвідношеннями:
, обумовлені рекурентними співвідношеннями:
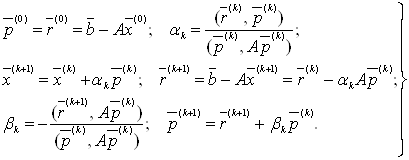 (20)
(20)
Для цих векторів мають місце наступні співвідношення:
![]() (21)
(21)
![]() (22)
(22)
Справді, у силу самої побудови при i (j
![]()
Далі, при i>j
![]()
Якщо i=j+1, то права частина дорівнює нулю, у силу визначення ![]() , якщо ж i>j+1, те
, якщо ж i>j+1, те![]() , по доведеному, і
, по доведеному, і
![]() .
.
Продовжуючи зниження індексу у вектора ![]() , через кілька кроків прийдемо до скалярного добутку
, через кілька кроків прийдемо до скалярного добутку ![]() (по визначенню
(по визначенню ![]() ). Таким чином, співвідношення (21) доведені. Для доказу (22), у силу рівноправності індексів i і j, припустимо, що i>j. Тоді
). Таким чином, співвідношення (21) доведені. Для доказу (22), у силу рівноправності індексів i і j, припустимо, що i>j. Тоді
![]() .
.
Тому що в n-мірному векторному простори не може бути більше n взаємно ортогональних векторів, то на деякому кроці ![]() одержимо
одержимо ![]() , тобто
, тобто ![]() буде рішенням системи (1).
буде рішенням системи (1).
На мал. 1 показана геометрична картина нашої побудови при n=3.
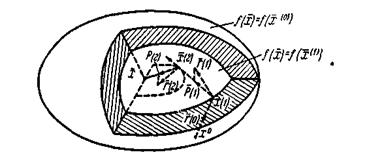
Мал. 1
0 комментариев