Линейные системы над конечными коммутативными кольцами

1.3 Линейные системы над конечными коммутативными кольцами

Теорема в предыдущей части показывает что для того чтобы решить, будет ли данная мономиальная система , над конечной областью , системой с конечными элементами, достаточно решить этот вопрос для связанных булевых систем, для которых определена линейная система над конечным кольцом . Поэтому остаётся развить критерий для линейных систем над конечными коммутативными кольцами, для того чтобы решить будет ли система – системой конечных элементов. Здесь мы сведем общий случай  к  имеющему первичную мощность.

Путь  для взаимно простых целых чисел  и , и пусть  –линейная система для  размерности . Выбрав изоморфизм  получим, что  – изоморфно к произведению , где  и  – линейные системы над  и , соответственно. Используя факт того, что фазовое пространство  является прямым произведением тогда, когда ориентированы графы фазовых пространств для  и , мы получаем следующий результат.

Предположение 1.3.1.

Пусть  для взаимно простых целых чисел  и , и пусть  – линейная система над  размерности . Пусть  и  – линейные преобразования над  и , соответственно. Тогда  – система конечных элементов тогда, и только тогда, когда  и  – системы конечных элементов.

Имея цель развить критерий для изучения систем конечных элементов, достаточно изучить линейные системы над кольцами вида  для простых чисел . Следующая теорема обеспечивает критерий для дальнейшего решения проблемы с линейной системой над областью простых чисел .

Теорема 1.3.1.

Пусть  – линейное отображение, и пусть  – проекционное отображение  на . Тогда , где . Тогда фазовое пространство  – изоморфно подграфу фазового пространства .

Доказательство.

Пусть  определяется . Тогда легко проверить что , так как  – линейные отображения для всех . Поэтому, прямо проверяется что  тогда, и только тогда, когда , и, следовательно, фазовое пространство  изоморфно подграфу фазового пространства .

Следствие 1.3.1.

Пусть  – линейное отображение, и пусть  – проекционное отображение  на . Если  не является системой конечных элементов, тогда  – не является системой конечных элементов.

Пример 1.3.1.

Пусть  определяется . Тогда .

- состоит из всех возможных наборов длины 2 из четырёх элементов: 0, 1, 2,3.

Это наборы:

Используя функцию , определим переходы в фазовом пространстве .

00 - ,

01 - ,

02 - ,

03 - ,

10 - ,

11 - ,

12 - ,

13 - ,

20 - ,

21 - ,

22 - ,

23 - ,

30 - ,

31 - ,

32 - ,

33 - .

Так как , переходы в фазовом пространстве  определены следующим образом.

00 - ,

01 - ,

10 - ,

11 - .

Фазовые пространства  и  изображены на рисунках 1.3.1 и 1.3.2, соответственно.

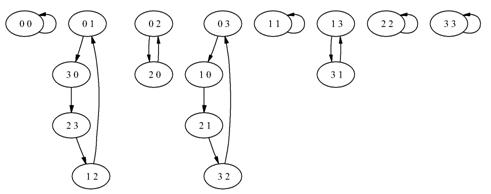
Рис. 1.3.1. Фазовое пространство .

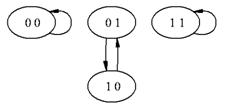
Рис. 1.3.2. Фазовое пространство .

ЗАКЛЮЧЕНИЕ

Результат позволяет изучить динамику линейных систем над конечными кольцами, в частности для нахождения критерия для линейной системы быть системой конечных элементов. Также обеспечивается алгоритм решения того, чтобы мономиальная система над произвольной конечной областью была системой конечных элементов. Однако, пока, трудно изучается даже динамика линейных систем над кольцам вида , из-за недостатка уникальной факторизации в полиномиальном кольце .

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.  Colon-Reyes O., Jarrah A., Laubenbacher R., Sturmfels B. Monomial dynamical systems over finite fields// Complex Systems. 2006. Том 16, стр. 333-342.