Навигация
Числовые характеристики случайных величин
1.5 Числовые характеристики случайных величин
Законы распределения полностью характеризуют случайные величины, но их не всегда можно получить. Случайные величины достаточно полно можно охарактеризовать, зная их числовые характеристики, которые определяются с помощью так называемых моментов (начальных, центральных и смешанных).
Начальные моменты
Начальные моменты характеризуют отклонение случайной величины относительно начала отсчета
 , (1.12)
, (1.12)
где f(x) –плотность вероятности случайной величины X.
При к = 1
 . (1.13)
. (1.13)
Математическим ожиданием случайной величины mx называется начальный момент первого порядка a1, который характеризует среднее значение случайной величины.
Для дискретных, случайных величин
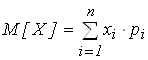 , (1.14)
, (1.14)
где xi и pi - возможные значения случайных величин и их вероятности.
Для любой функции случайного аргумента математическое ожидание равно
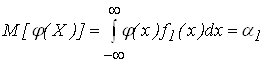 . (1.15)
. (1.15)
Для функции двух случайных аргументов математическое ожидание равно
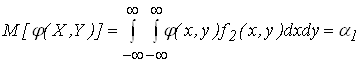 . (1.16)
. (1.16)
При к = 2
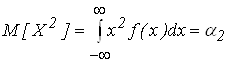 . (1.17)
. (1.17)
Средним квадратом случайной величины называется начальный момент второго порядка -a2, который характеризует среднюю мощность случайной величины.
Центральные моменты
Центральные моменты характеризуют отклонение случайной величины относительно среднего значения.
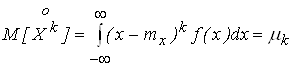 . (1.18)
. (1.18)
![]() называется центрированной величиной.
называется центрированной величиной.
При к = 1
 . (1.19)
. (1.19)
При к = 2
 . (1.20)
. (1.20)
Дисперсией случайной величины Dx называется центральный момент второго порядка -m1, который характеризует степень рассеивания случайной величины относительно среднего значения.
Величина ![]() называется средним квадратичным отклонением.
называется средним квадратичным отклонением.
Между моментами существует следующая связь:
![]() . (1.21)
. (1.21)
Смешанные центральные моменты
Корреляционный момент - kxy характеризуют статистическую зависимость между случайными величинами X и Y.
 (1.22)
(1.22)
На практике часто используется безразмерная величина, называемая коэффициентом корреляции
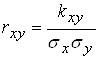 . (1.23)
. (1.23)
Случайные величины X и Y называют коррелированными, если kxy ¹ 0, и некоррелированными, если kxy = 0.
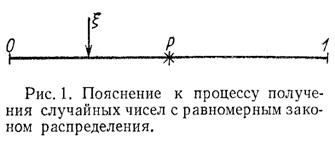
Пример 1.1. Определить функцию распределения и числовые характеристики для случайной величины с равномерной плотностью вероятности, график которой приведен на рис. 1.5.
Решение:![]() Функцию распределения можно определить из соотношения
Функцию распределения можно определить из соотношения
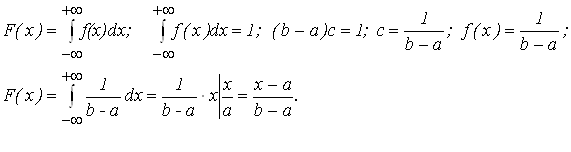
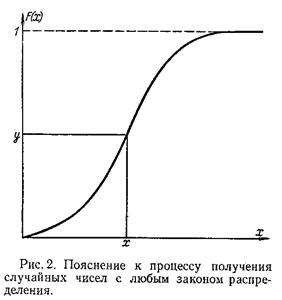
При этом функция распределения имеет вид (рис. 1.6).

Рис. 1.5 Рис. 1.6
Определим числовые характеристики.
Математическое ожидание
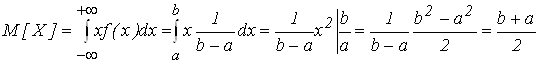 .
.
Средний квадрат

Дисперсия
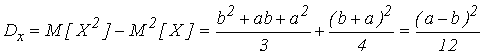 .
.
2. Случайные процессы и их статистические характеристики
Случайным (стохастическим) процессом называют случайную функцию, аргументом которой является время.
Реализацией называется неслучайная функция времени xi(t), которая является возможным значением случайного процесса X(t).
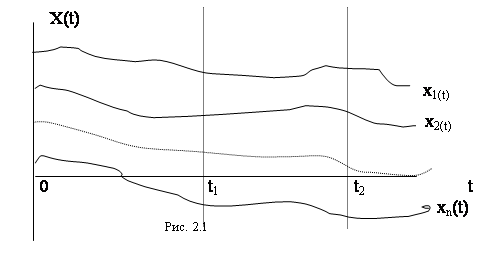 |
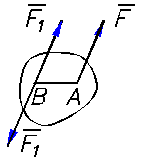
Группа возможных реализаций составляет множество, семейство или ансамбль (рис 2.1).
Сечением случайного процесса в момент времени t1 называются возможные значения случайного процесса X(t1) в момент времени t1.
Статистические методы изучают не каждую из реализаций xi(t1), образующих множество X(t), а свойство всего множества с помощью усреднения свойств его реализаций. Усреднение может выполняться по множеству и по времени.
Усреднение по множеству ![]() выполняется над множеством реализаций в фиксированный момент времени.
выполняется над множеством реализаций в фиксированный момент времени.
Усреднение по времени ![]() выполняется над одной реализаций на протяжении достаточно длинного промежутка времени –Т.
выполняется над одной реализаций на протяжении достаточно длинного промежутка времени –Т.
Для случайных процессов функция распределения и плотность вероятности полностью определяет статистические свойства процессов и зависит как от уровня -х, так и времени -t.
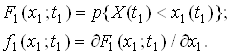 (2.1)
(2.1)
Эти функции характеризуют случайный процесс в фиксированный момент времени -t1.
Для полной характеристики случайного процесса в произвольные моменты времени необходимо знать многомерные законы.
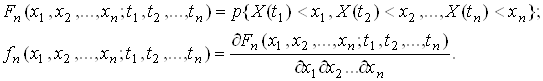 (2.2)
(2.2)
Эти законы громоздки, и оперировать ими сложно, поэтому на практике часто достаточно знание одномерных или двумерных законов. Это справедливо для широкого класса так называемых Гаусcовских процессов, или процессов с нормальным законом распределения. Например, помехи в САУ, действие которых обусловлено многими случайными факторами подчиненным различным законам распределения, и чем больше множество таких факторов, тем в значительно большей мере процесс будет приближаться к нормальному закону (в соответствии с центральной предельной теоремой).
Похожие работы
... . Деятельность формирует психические процессы. Любая деятельность – это соединение внутренних и внешних поведенческих действий и операций. Мы рассмотрим каждый вид психической деятельности отдельно. 2. Психические процессы как форма деятельности Психические процессы – общее название ощущений, восприятий, приспособлений, внимания, памяти, мышления, воображения, речи. Все они участвуют в ...
... (Балаша-Фора-Мальгранжа, Черенина, Джефферсона, Хиллиера и др.) являются модификациями метода ветвей и границ с учётом специфики условий задачи. 4. Построение оптимальной последовательности заданий на обработку в узле вычислительной системы 4.1 Формализация вычислительного процесса и рабочей нагрузки Узел вычислительной системы представляется в виде совокупности оборудования и ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
... инструментарий исследования организационных отношений. 3.4 Заслуги А.А. Богданова в разработке организационной науки Главная заслуга российских исследователей - разработка фундаментальных методологических проблем теории организации. Одним из выдающихся ученых, внесших наиболее весомый вклад в разработку организационной науки, является А.А.Богданов (Малиновский) (1873 - 1928). Добытые и ...


0 комментариев