Навигация
2.1.2 Обратный ход
Обратный ход. Из последнего уравнения системы находим xn. Подставляя найденное значение xn в предпоследнее уравнение, получим xn–1. Осуществляя обратную подстановку, далее последовательно находим xn–1, xn–2, …, x1. Вычисления неизвестных здесь проводятся по формулам
xn = bn(n–1) / ann(n–1),
xk = (bn(k–1) – ak,k+1(k–1)xk+1 – akn(k–1)xn) / akk(k–1), (k = n – 1, , 1).
Заметим, что вычисление множителей, а также обратная подстановка требуют деления на главные элементы akk(k–1). Поэтому если один из главных элементов оказывается равным нулю, то схема единственного деления не может быть реализована. Здравый смысл подсказывает, что и в ситуации, когда все главные элементы отличны от нуля, но среди них есть близкие к нулю, возможен неконтролируемый рост погрешности.
2.2 Метод Гаусса с выбором главного элемента по столбцу
На k-м шаге прямого хода метода Гаусса с выбором главного элемента по столбцу коэффициенты уравнений системы с номерами i = k + 1, …, n преобразуются по формулам
aij(k) = aij(k–1) − qikakj , bi(k) = bi(k–1) − qikbk(k–1) , i = k + 1, …, n.
Интуитивно ясно, что во избежание сильного роста коэффициентов системы и связанных с этим ошибок нельзя допускать появления больших множителей qik.
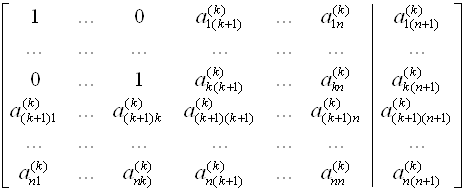
В методе Гаусса с выбором главного элемента по столбцу гарантируется, что
|qik| ≤ 1 для всех k = 1, 2, …, n – 1 и i = k + 1, …, n.
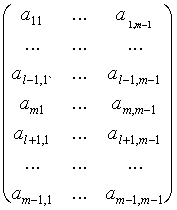
Отличие этого варианта метода Гаусса от схемы единственного деления заключается в том, что на k-м шаге исключения в качестве главного элемента выбирают максимальный по модулю коэффициент aikk при неизвестной xk в уравнениях с номерами i = k + 1, …, n. Затем соответствующее выбранному коэффициенту уравнение с номером ik меняют местами с k-м уравнением системы для того, чтобы главный элемент занял место коэффициента akk(k-1). После этой перестановки исключение неизвестного xk производят, как в схеме единственного деления.
3 Функциональные модели и блок-схемы решения задачи
Блок-схема решения задачи представлена на рисунке 1.
Условные обозначения:
· K – размерность матрицы;
· MATRIX – матрица;
· N – размерность матрицы;
· X – матрица решения СЛАУ;
· I_MAX – индекс максимального элемента в строке;
· J_MAX – индекс максимального элемента в столбце;
· OTV – массив позиций элементов;
· RES – вспомогательный массив;
· TEMP – временная переменная;
· GLAV_EL – функция, определяющая на какой позиции должен стоять главный элемент;
· INDEX – рабочая переменная.
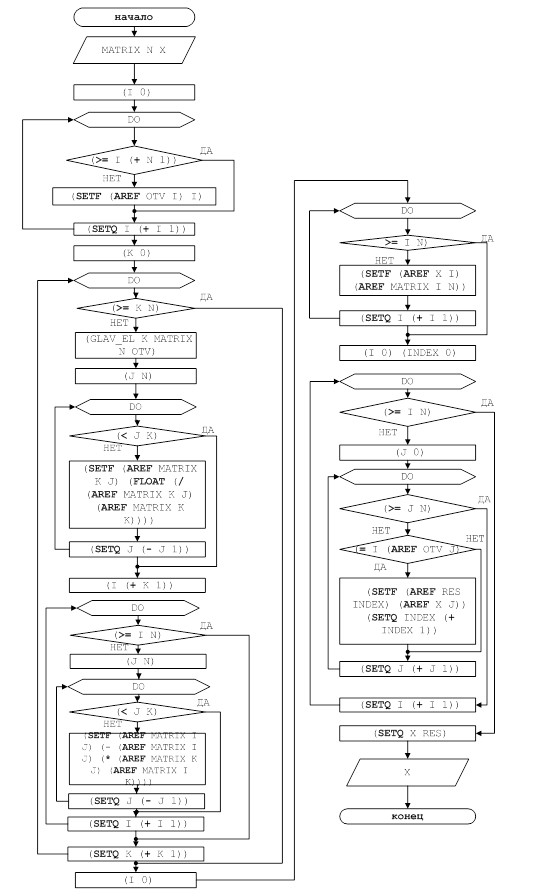
Рисунок 1 – Блок-схема решения задачи для функции GAUSS
\
4 Программная реализация решения задачи
ФУНКЦИЯ ПОИСКА МАКСИМАЛЬНОГО ЭЛЕМЕНТА И ПЕРЕСТАНОВКИ СТРОК И СТОЛБЦОВ
(DEFUN GLAV_EL (K MATRIX N X)
(DECLARE (SPECIAL I_MAX))
(DECLARE (SPECIAL J_MAX))
(DECLARE (SPECIAL TEMP))
(DECLARE (SPECIAL I))
(SETQ I_MAX K)
(SETQ J_MAX K)
;ИЩЕМ МАКСИМАЛЬНЫЙ ПО МОДУЛЮ ЭЛЕМЕНТ
(DO
((I K))
((>= I N))
(DO
((J K))
((>= J N))
(IF (< (ABS (AREF MATRIX I_MAX J_MAX)) (ABS (AREF MATRIX I J)))
(PROGN
(SETQ I_MAX I)
(SETQ J_MAX J)
)
)
(SETQ J (+ J 1))
)
(SETQ I (+ I 1))
)
;ПЕРЕСТАВЛЯЕМ СТРОКИ
(DO
((J K))
((>= J (+ N 1)))
(SETQ TEMP (AREF MATRIX K J))
(SETF (AREF MATRIX K J) (AREF MATRIX I_MAX J))
(SETF (AREF MATRIX I_MAX J) TEMP)
(SETQ J (+ J 1))
)
;ПЕРЕСТАВЛЯЕМ СТОЛБЦЫ
(DO
((I 0))
((>= I N))
(SETQ TEMP (AREF MATRIX I K))
(SETF (AREF MATRIX I K) (AREF MATRIX I J_MAX))
(SETF (AREF MATRIX I J_MAX) TEMP)
(SETQ I (+ I 1))
)
;УЧИТЫВАЕМ ИЗМЕНЕНИЕ ПОРЯЛКА КОРНЕЙ
(SETQ I (AREF X K))
(SETF (AREF X K) (AREF X J_MAX))
(SETF (AREF X J_MAX) I)
)
(DEFUN GAUSS (MATRIX N X)
(DECLARE (SPECIAL OTV))
(DECLARE (SPECIAL RES))
(SETQ OTV (MAKE-ARRAY 50 :ELEMENT-TYPE 'INTEGER :INITIAL-ELEMENT 0))
(SETQ RES (MAKE-ARRAY N :ELEMENT-TYPE 'INTEGER :INITIAL-ELEMENT 0))
;СНАЧАЛА ВСЕ КОРНИ ПО ПОРЯДКУ
(DO
((I 0))
((>= I (+ N 1)))
(SETF (AREF OTV I) I)
(SETQ I (+ I 1))
)
;ПРЯМОЙ ХОД МЕТОДА ГАУССА
(DO
((K 0))
((>= K N))
;ОПРЕДЕЛЯЕМ НА КАКОЙ ПОЗИЦИИ ДОЛЖЕН СТОЯТЬ ГЛАВНЫЙ ЭЛЕМЕНТ
(GLAV_EL K MATRIX N OTV)
(IF (< (ABS (AREF MATRIX K K)) 0.0001) (PRINT "SYSTEMA NE IMEET EDINSTVENNOGO RESHENIYA"))
(DO
((J N))
((< J K))
(SETF (AREF MATRIX K J) (FLOAT (/ (AREF MATRIX K J) (AREF MATRIX K K))))
(SETQ J (- J 1))
)
(DO
((I (+ K 1)))
((>= I N))
(DO
((J N))
((< J K))
(SETF (AREF MATRIX I J) (- (AREF MATRIX I J) (* (AREF MATRIX K J) (AREF MATRIX I K))))
(SETQ J (- J 1))
)
(SETQ I (+ I 1))
)
(SETQ K (+ K 1))
)
;ОБРАТНЫЙ КОД
(DO
((I 0))
((>= I N))
(SETF (AREF X I) (AREF MATRIX I N))
(SETQ I (+ I 1))
)
(DO
((I (- N 2)))
((< I 0))
(DO
((J (+ I 1)))
((>= J N))
(SETF (AREF X I) (- (AREF X I) (* (AREF X J) (AREF MATRIX I J))))
(SETQ J (+ J 1))
)
(SETQ I (- I 1))
)
(DO
((I 0) (INDEX 0))
((>= I N) RES)
(DO
((J 0))
((>= J N))
;РАССТАВЛЯЕМ КОРНИ ПО ПОРЯДКУ
(IF (= I (AREF OTV J))
(PROGN
(SETF (AREF RES INDEX) (AREF X J))
(SETQ INDEX (+ INDEX 1))
)
)
(SETQ J (+ J 1))
)
(SETQ I (+ I 1))
)
(SETQ X RES)
)
(SETQINPUT_STREAM(OPEN " D:\GAUSS_MATRIX.TXT" :DIRECTION :INPUT))
;ПОЛУЧАЕМ РАЗМЕРНОСТЬ МАТРИЦЫ
(SETF N (READINPUT_STREAM))
;ПОЛУЧАЕМ МАТРИЦУ
(SETF MATRIX (READINPUT_STREAM))
(CLOSEINPUT_STREAM)
(SETQ X (MAKE-ARRAY 50 :ELEMENT-TYPE 'INTEGER :INITIAL-ELEMENT 0))
(SETQ RES (GAUSS MATRIX N X))
;ЗАПИСЫВАЕМ КОРНИ СЛАУ В ФАЙЛ
(SETQOUTPUT_STREAM(OPEN " D:\KORNI_SLAY.TXT" :DIRECTION :OUTPUT))
(PRINT RES OUTPUT_STREAM)
(TERPRIOUTPUT_STREAM)
(CLOSEOUTPUT_STREAM)
5 Пример выполнения программы
Пример 1.
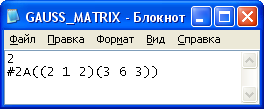
Рисунок 2 – Входные данные
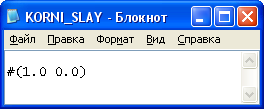
Рисунок 3 – Выходные данные
Пример 2.
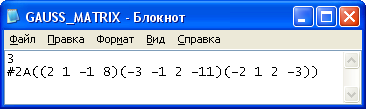
Рисунок 4 – Входные данные
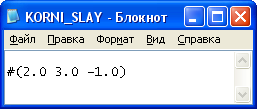
Рисунок 5 – Выходные данные
Пример 3.

Рисунок 6 – Входные данные
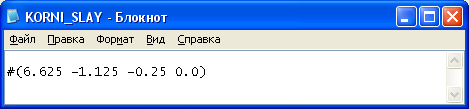
Рисунок 7 – Выходные данные
ЗАКЛЮЧЕНИЕ
Проблема повышения качества вычислений, как несоответствие между желаемым и действительным, существует и будет существовать в дальнейшем. Ее решению будет содействовать развитие информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования.
Итогом работы можно считать созданную функциональную модель численного решения системы линейных уравнений с помощью метода исключения Гаусса с выбором главного элемента по столбцу. Созданная функциональная модель и ее программная реализация могут служить органической частью решения более сложных задач.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ и литературы
1. Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов [Текст] / И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, 2007. – 708 с.
2. Васильев, Ф.П. Численные методы решения экстремальных задач. [Текст] / Ф.П. Васильев – М.: Наука, 2002. C. 415.
3. Высшая документация – Online документация [Электронный ресурс] – Режим доступа: http://vm.psati.ru/online-vmath/index.php?page=8
4. Калиткин, Н.Н. Численные методы. [Электронный ресурс] / Н.Н. Калиткин. – М.: Питер, 2001. С. 504.
5. Кнут, Д.Э. Искусство программирования. Основные алгоритмы [Текст] / Д.Э. Кнут. – М.: Вильямс, 2007. Т.1.– 712 с.
6. Метод Гаусса [Электронный ресурс] – Режим доступа: http://www.wikipedia.org/wiki/Метод_Гаусса.
7. Симанков, В.С. Основы функционального программирования [Текст] / В.С. Симанков, Т.Т. Зангиев, И.В. Зайцев. – Краснодар: КубГТУ, 2002. – 160 с.
8. Степанов, П.А. Функциональное программирование на языке Lisp. [Электронный ресурс] / П.А.Степанов, А.В. Бржезовский. – М.: ГУАП, 2003. С. 79.
9. Хювенен Э. Мир Лиспа [Текст] / Э. Хювенен, Й. Сеппянен. – М.: Мир, 1990. – 460 с.
Похожие работы
... Вывод Программа, разработанная в данной курсовой работе, реализует метод Зейделя для решения СЛАУ 6-го порядка. Она даёт гарантированно правильное решение системы линейных уравнений, если каждый элемент главной диагонали матрицы коэффициентов является единственным максимальным в своей строке, ненулевым, либо справедливы условия: максимальный элемент строки является единственным максимальным в ...
... , ary2s Типы данных для переменных, в которых хранятся значения коэффициентов системы Unit2 Gauss1 Процедура для решения системы линейных уравнений методом Гаусса Unit2 Gaussj Процедура для решения системы линейных уравнений методом Жордана-Гаусса Unit2 i,j,l Счетчики Unit1 prover Промежуточная переменная типа String, используется для проверки наличия букв среди коэффициентов ...
... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...
... на главной и двух побочных диагоналях, равны нулю при та В общем случае системы линейных алгебраических уравнений с трехдиагональной матрицей имеют вид Для численного решения систем трехдиагональными матрицами применяется метод прогонки, который представляет собой вариант метода последовательного исключения неизвестных. Т.е. матрицу А можно записать Идея метода прогонки состоит в ...








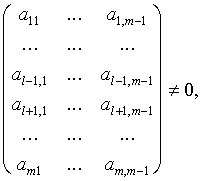
0 комментариев