Навигация
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
2. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
2.1. Теоретическое введение
Графический метод довольно прост и нагляден для решения задач линейного программирования с двумя переменными. Он основан на геометрическом представлении допустимых решений и ЦФ задачи.
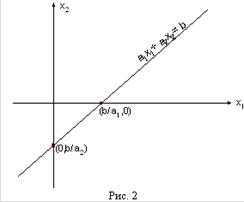
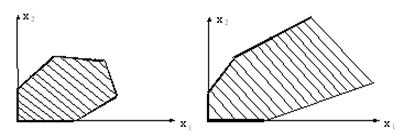
Каждое из неравенств задачи линейного программирования (1.2) определяет на координатной плоскости ![]() некоторую полуплоскость (рис.2.1), а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучом, одной точкой. В случае несовместности системы ограничений задачи (1.2) ОДР является пустым множеством.
некоторую полуплоскость (рис.2.1), а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучом, одной точкой. В случае несовместности системы ограничений задачи (1.2) ОДР является пустым множеством.
Все вышесказанное относится и к случаю, когда система ограничений (1.2) включает равенства, поскольку любое равенство
![]()
можно представить в виде системы двух неравенств (см. рис.2.1)
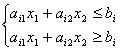
ЦФ ![]() при фиксированном значении
при фиксированном значении ![]() определяет на плоскости прямую линию
определяет на плоскости прямую линию ![]() . Изменяя значения L, мы получим семейство параллельных прямых, называемых линиями уровня.
. Изменяя значения L, мы получим семейство параллельных прямых, называемых линиями уровня.
Это связано с тем, что изменение значения L повлечет изменение лишь длины отрезка, отсекаемого линией уровня на оси ![]() (начальная ордината), а угловой коэффициент прямой
(начальная ордината), а угловой коэффициент прямой ![]() останется постоянным (см.рис.2.1). Поэтому для решения будет достаточно построить одну из линий уровня, произвольно выбрав значение L.
останется постоянным (см.рис.2.1). Поэтому для решения будет достаточно построить одну из линий уровня, произвольно выбрав значение L.
Вектор ![]() с координатами из коэффициентов ЦФ при
с координатами из коэффициентов ЦФ при ![]() и
и ![]() перпендикулярен к каждой из линий уровня (см. рис.2.1). Направление вектора
перпендикулярен к каждой из линий уровня (см. рис.2.1). Направление вектора ![]() совпадает с направлением возрастания ЦФ, что является важным моментом для решения задач. Направление убывания ЦФ противоположно направлению вектора
совпадает с направлением возрастания ЦФ, что является важным моментом для решения задач. Направление убывания ЦФ противоположно направлению вектора![]() .
.
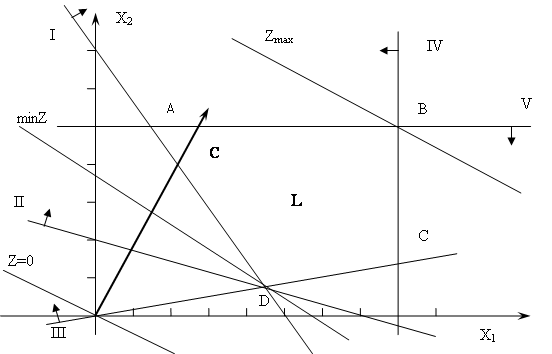
Суть графического метода заключается в следующем. По направлению (против направления) вектора ![]() в ОДР производится поиск оптимальной точки
в ОДР производится поиск оптимальной точки ![]() . Оптимальной считается точка, через которую проходит линия уровня
. Оптимальной считается точка, через которую проходит линия уровня ![]() , соответствующая наибольшему (наименьшему) значению функции
, соответствующая наибольшему (наименьшему) значению функции ![]() . Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.
. Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.
При поиске оптимального решения задач линейного программирования возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений – единственная точка; задача не имеет решений.
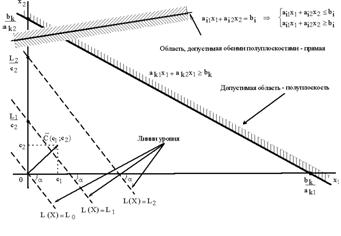
Рисунок 2.1 Геометрическая интерпретация ограничений и ЦФ задачи.
2.2. Методика решения задач ЛП графическим методом.
I. В ограничениях задачи (1.2) заменить знаки неравенств знаками точных равенств и построить соответствующие прямые.
II. Найти и заштриховать полуплоскости, разрешенные каждым из ограничений-неравенств задачи (1.2). Для этого нужно подставить в конкретное неравенство координаты какой-либо точки [например, (0;0)], и проверить истинность полученного неравенства.
Если неравенство истинное,
то надо заштриховать полуплоскость, содержащую данную точку;
иначе (неравенство ложное) надо заштриховать полуплоскость, не содержащую данную точку.
Поскольку ![]() и
и ![]() должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси
должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси ![]() и правее оси
и правее оси ![]() , т.е. в I-м квадранте.
, т.е. в I-м квадранте.
Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой. Поэтому необходимо выделить на графике такие прямые.
III. Определить ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделить ее. При отсутствии ОДР задача не имеет решений.
IV. Если ОДР – не пустое множество, то нужно построить целевую прямую, т.е. любую из линий уровня ![]() (где L – произвольное число, например, кратное
(где L – произвольное число, например, кратное ![]() и
и ![]() , т.е. удобное для проведения расчетов). Способ построения аналогичен построению прямых ограничений.
, т.е. удобное для проведения расчетов). Способ построения аналогичен построению прямых ограничений.
V. Построить вектор ![]() , который начинается в точке (0;0) и заканчивается в точке
, который начинается в точке (0;0) и заканчивается в точке ![]() . Если целевая прямая и вектор
. Если целевая прямая и вектор ![]() построены верно, то они будут перпендикулярны.
построены верно, то они будут перпендикулярны.
VI. При поиске максимума ЦФ необходимо передвигать целевую прямую в направлении вектора ![]() , при поиске минимума ЦФ – против направления вектора
, при поиске минимума ЦФ – против направления вектора ![]() . Последняя по ходу движения вершина ОДР будет точкой максимума или минимума ЦФ. Если такой точки (точек) не существует, то можно сделать вывод о неограниченности ЦФ на множестве планов сверху (при поиске максимума) или снизу (при поиске минимум).
. Последняя по ходу движения вершина ОДР будет точкой максимума или минимума ЦФ. Если такой точки (точек) не существует, то можно сделать вывод о неограниченности ЦФ на множестве планов сверху (при поиске максимума) или снизу (при поиске минимум).
VII. Определить координаты точки max (min) ЦФ ![]() и вычислить значение ЦФ
и вычислить значение ЦФ ![]() . Для вычисления координат оптимальной точки
. Для вычисления координат оптимальной точки ![]() необходимо решить систему уравнений прямых, на пересечении которых находится
необходимо решить систему уравнений прямых, на пересечении которых находится ![]() .
.
3. ПРИМЕНЕНИЕ ГРАФИЧЕСКОГО МЕТОДА РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ НА ПРАКТИКЕ.
3.1 Экономическая постановка задачи линейного программирования
Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем первой линии - 60 изделий, второй линии - 80 изделий. На радиоприемник первой модели расходуется 15 однотипных элементов электронных схем, на радиоприемник второй модели - 10 таких же элементов. Максимальный суточный запас используемых элементов равен 950 единиц. Прибыли от реализации одного радиоприемника первой и второй моделей равны 40$ и 20$ соответственно. Определите оптимальные суточные объемы производства первой и второй моделей на основе графического решения задачи.
Похожие работы
... . 1.3. Построение ограничений и градиента целевой функции : 1.4. Область допустимых решений – отрезок AB. 1.5. Точка А – оптимальная. Координаты т. А: ; ; . 2. Решение задачи линейного программирования симплекс-методом. Прямая задача. Задачу линейного программирования для любой вершины в компактной форме можно представить в виде: Для получения используем алгоритм, приведённый в ...
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
... задачи f1(x)=max[g1(x)]=g1(x) – для первого предприятия; - для остальных предприятий. Решение задачи оптимального распределения средств между предприятиями методом динамического программирования Таблица 12 Средства с, тыс. гр. Предприятие 1 2 3 4 G1(x) G2(x) G3(x) G4(x) 20 11 13 12 10 40 21 20 22 27 60 40 42 34 33 80 54 45 55 57 100 62 62 ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
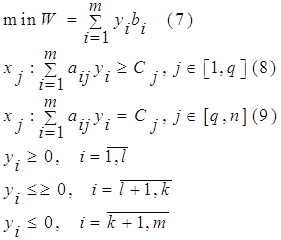

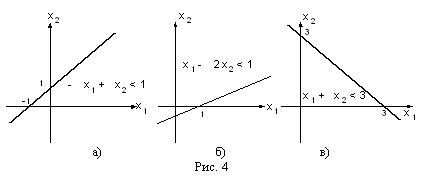
0 комментариев