Навигация
Решение задач нелинейного программирования
Министерство науки и образования Республики Казахстан
Талдыкорганский политехнический колледж
Курсовая работа
По предмету:
«Моделирование производственных и экономических процессов»
На тему:
«Решение задач нелинейного программирования»
г. Талдыкорган 2007 г.
Введение
Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи математического программирования формулируются следующим образом: найти экстремум некоторой функции многих переменных f (x1, x2,…, xn) при ограничениях gi (x1, x2,…, xn) bi, где gi – функция, описывающая ограничения, а bi – действительное число, i = 1,…, m. Функция f называется функцией цели (целевой функцией).
В общем, виде задача нелинейного программирования состоит в определении максимального (минимального) значения функции f(x1, x2, …, xn) при условии, что ее переменные удовлетворяют соотношениям:
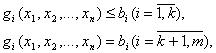
где f и g – некоторые известные функции n переменных, а bi – заданные числа.
В результате решения задачи будет определена точка Х*= (x1*, x2*, …, xn*), координаты которой удовлетворяют соотношениям и такая, что для всякой другой точки Х= (x1, x2, …, xn), удовлетворяющей условиям, выполняется неравенство f (x1*, x2*, …, xn*) ≥ f (x1, x2, …, xn) [f (x1*, x2*, …, xn*) ≥ f (x1, x2, …, xn)].
Если f и gi – линейные функции, то задача является задачей линейного программирования.
Соотношения образуют систему ограничений и включают в себя условия не отрицательности переменных, если такие условия имеются. Условия неотрицательности переменных могут быть заданы и непосредственно.
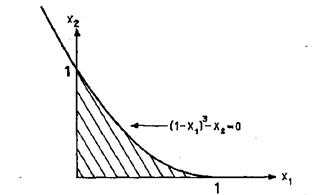
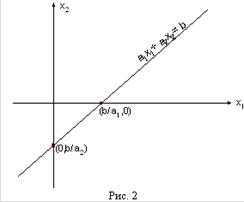
В евклидовом пространстве Еnсистема ограничений определяет область решений задачи. В отличие от задачи линейного программирования она не всегда является выпуклой.
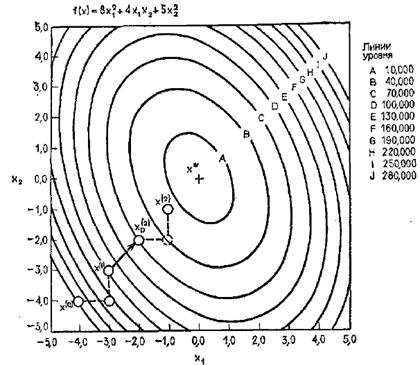
Если определена область допустимых решений, то нахождение решения задачи сводится к определению такой точки этой области, через которую проходит гиперповерхность наивысшего (наименьшего) уровня: f (x1, x2, …, xn) = h. Указанная точка может находиться как на границе области допустимых решений, так и внутри неё.
Процесс нахождения решения задачи нелинейного программирования с использованием ее геометрической интерпретации включает следующие этапы:
1. Находят область допустимых решений задачи, определяемую соотношениями (если она пуста, то задача не имеет решения).
2. Строят гиперповерхность f (x1, x2, …, xn) = h.
3. Определяют гиперповерхность наивысшего (наинизшего) уровня или устанавливают неразрешимость задачи из-за неограниченности функций сверху (внизу) на множестве допустимых решений.
4. Находят точку области допустимых решений, через которую проходит гиперповерхности наивысшего (наинизшего) уровня, и определяют в ней значение функции.
Или приводят задачу нелинейного программирования к задаче линейного программирования и решают нижеизложенными способами.
Задача является задачей линейного программирования, а следовательно, ее решение можно найти известными методами: 1) графический; 2) табличный (прямой, простой) симплекс – метод; 3) метод искусственного базиса; 4) модифицированный симплекс – метод; 5) двойственный симплекс – метод.
1. Табличный симплекс-метод
Для его применения необходимо, чтобы знаки в ограничениях были вида «меньше либо равно», а компоненты вектора b – положительны.
Алгоритм решения сводится к следующему:
1. Приведение системы ограничений к каноническому виду путём введения дополнительных переменных для приведения неравенств к равенствам.
2. Если в исходной системе ограничений присутствовали знаки» равно "или" больше либо равно», то в указанные ограничения добавляются искусственные переменные, которые так же вводятся и в целевую функцию со знаками, определяемыми типом оптимума.
3. Формируется симплекс – таблица.
4. Рассчитываются симплекс – разности.
5. Принимается решение об окончании либо продолжении счёта.
6. При необходимости выполняются итерации.
7. На каждой итерации определяется вектор, вводимый в базис, и вектор, выводимый из базиса. Таблица пересчитывается по методу Жордана – Гаусса или каким-нибудь другим способом.
2. Метод искусственного базиса
Данный метод решения применяется при наличии в ограничении знаков «равно» больше либо равно» меньше либо равно и является модификацией табличного метода. Решение системы производится путём ввода искусственных переменных со знаком, зависящим от типа оптимума, т.е. для исключения из базиса этих переменных последние вводятся в целевую функцию с большими отрицательными коэффициентами, а в задачи минимизации – с положительными. Таким образом, из исходной задачи получается новая задача.
Если в оптимальном решении – задачи нет искусственных переменных, это решение есть оптимальное решение исходной задачи. Если же в оптимальном решении – задачи хоть одна из искусственных переменных будет отлична от нуля, то система ограничений исходной задачи несовместна и исходная задача неразрешима.
Похожие работы
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...
... нахождение точки Куна—Таккера обеспечивает получение оптимального решения задачи нелинейного программирования. Теорему 2 можно также использовать для доказательства оптимальности данного решения задачи нелинейного программирования. В качестве иллюстрации опять рассмотрим пример: Минимизировать при ограничениях С помощью теоремы 2 докажем, что решение является оптимальным. Имеем Так ...
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...

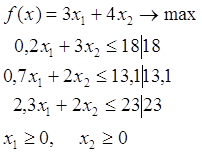
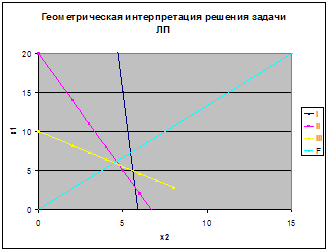
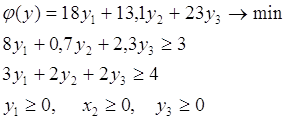
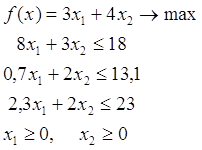
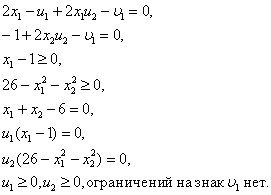

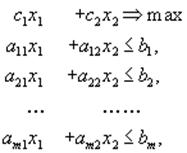
0 комментариев