Навигация
1.1 Проверка чётности
Контроль четности или коррекция ошибок (ECC (код исправления ошибок)) используется в основном только в жизненно важных компьютерных системах, где недопустима даже одна ошибка в несколько десятилетий. Проверка четности – довольно простой метод обнаружения ошибок памяти, без возможности восстановления. Каждый байт данных связан с одним битом четности или так называемым паритетным битом. Этот бит устанавливается во время записи, и затем рассчитывается и сравнивается во время чтения. Изменение состояния этого бита говорит о возникшей ошибке. Этот метод ограничен определением изменения состояния одиночного бита в байте. В случае изменения состояния двух битов, возможна ситуация, когда вычисление паритетного бита совпадет с записанным. В этом случае система не определит ошибку, и произойдет экстренная остановка системы. Так как приблизительно 90% всех нерегулярных ошибок происходит именно с одиночным разрядом, проверки четности бывает достаточно для большинства ситуаций. К сожалению необходимость в дополнительных вычислениях паритетного бита требует некоторых затрат процессорного времени, что несколько снижает производительность всей системы. Более интересным методом проверки ошибок работы памяти является т.н. ECC или коррекция ошибок или код исправления ошибок. Этот метод включает определение ошибки не только в одиночном разряде, но и двух, трех и четырех разрядах. Кроме того ECC может также исправлять ошибку в одиночном разряде. ECC может быть реализован или на модуле памяти (ECC – on – Simm, или EOS) или в чипсете. Однако модули EOS встречаются крайне редко. ECC основывается на алгоритме «хешинга», который работает одновременно с 8 байтами (64 бита), и размещает результат в 8-ми разрядное ECC слово. Во время считывания результат ECC слова сравнивается с рассчитанным, подобно тому, как происходит в методе проверки четности. Основное различие состоит в том, что в проверке четности каждый бит связан с одним байтом, в то время как ECC слово связана со всеми 8 байтами. Это означает, что разрядные значения для ECC не будут теми же, что и индивидуальные биты для проверки четности для тех же восьми байтов, поэтому модули ECC не могут использоваться в режиме четности (однако, паритетные модули, могут использоваться в режиме ECC, как описано ниже). ECC модули могут использоваться на не паритетный и на ECC/ non-ECC платах. Модуль ECC не может использоваться в режиме проверки четности. Причина этого является схемотехническая реализация модуля ECC. Он не может устанавливать отдельные биты, поэтому чипсет не будет записывать правильные данные в ECC слово.
1.2 Код CRC
Методы обнаружения ошибок предназначены для выявления повреждений со общений при их передаче по зашумленным каналам (вносящих эти ошибки). Для этого передающее устройство создает некоторое число, называемое контрольной суммой и являющееся функцией сообщения, и добавляет его к этому сообщению. Приемное устройство, используя тот же самый алгоритм, рассчитывает контрольную сумму принятого сообщения и сравнивает ее с переданным значением. Например, если для расчета контрольной суммы используем простое сложение байтов сообщения по модулю 256, то может возникнуть примерно следующая ситуация. (Все числа примера десятичные.)
Сообщение: 6 23 4
Сообщение с контрольной суммой: 6 23 4 33
Сообщение после передачи: 6 27 4 33
Как видно, второй байт сообщения при передаче оказался измененным с 23 на 27. Приемник может обнаружить ошибку, сравнивая переданную контрольную сумму (33) с рассчитанной им самим: 6 + 27 + 4 = 37. Если при правильной передаче сообщения окажется поврежденной сама контрольная сумма, то такое сообщение будет неверно интерпретировано, как искаженное. Однако, это не самая плохая ситуация. Более опасно, одновременное повреждение сообщения и контрольной суммы таким образом, что все сообщение можно посчитать достоверным. К сожалению, исключить такую ситуацию невозможно, и лучшее, чего можно добиться, это снизить вероятность ее появления, увеличивая количество информации в контрольной сумме (например, расширив ее с одного до 2 байт).
Ошибки иного рода возникают при сложных преобразованиях сообщения для удаления из него избыточной информации. Однако, данная статья посвящена только расчетам CRC, которые относятся к классу алгоритмов, не затрагивающих само го сообщения и лишь добавляющих в его конце контрольную сумму:
<исходное неизмененное сообщение> <контрольная сумма>
Требования сложности
Выше показано, что повреждение сообщения может быть обнаружено, используя в качестве алгоритма контроля простое суммирование байтов сообщения по модулю 256:
Сообщение: 6 23 4
Сообщение с контрольной суммой: 6 23 4 33
Сообщение после передачи: 6 27 4 33
Недостаток этого алгоритма в том, что он слишком прост. Если произойдет несколько искажений, то в 1 случае из 256 не сможем их обнаружить. Например:
Сообщение: 6 23 4
Сообщение с контрольной суммой: 6 23 4 33
Сообщение после передачи: 8 20 5 33
Для повышения надежности можно было бы изменить размер регистра с 8 битного на 16 битный (то есть суммировать по модулю 65536 вместо модуля 256), что скорее всего снизит вероятность ошибки с 1/256 до 1/65536. Хотя это и неплохая идея, однако, она имеет тот недостаток, что применяемая формула расчета не "случайна" в должной степени — каждый суммируемый байт оказывает влияние лишь на один байт суммирующего регистра, при этом ширина самого регистра не имеет никакого значения. Например, во втором случае суммирующий регистр мог бы иметь ширину хоть мегабайт, однако ошибка все равно не была бы обнаружена. Проблема может быть решена лишь заменой простого суммирования более сложной функцией, чтобы каждый новый байт оказывал влияние на весь регистр контрольной суммы.
Таким образом, сформулировано 2 требования для формирования надежной контрольной суммы:
Ширина: Размер регистра для вычислений должен обеспечивать изначальную низкую вероятность ошибки (например, 32 байтный регистр обеспечивает вероятность ошибки 1/232).
Случайность: Необходим такой алгоритм расчета, когда каждый новый байт может оказать влияние на любые биты регистра.
Обратим внимание, что термин "контрольная сумма" изначально описывал достаточно простые суммирующие алгоритмы, однако, в настоящее время он используется в более широком смысле для обозначения сложных алгоритмов рас чета, таких как CRC. Алгоритмы CRC, которые и будем рассматривать в дальнейшем, очень хорошо удовлетворяют второму условию и, кроме того, могут быть адаптированы для работы с различной шириной контрольной суммы.
Контрольная сумма (Checksum) – Число, которое является функцией некоторого сообщения. Буквальная интерпретация данного слова указывает на то, что выполняется простое суммирование байтов сообщения, что, по видимому, и делалось в ран них реализациях расчетов. Однако, на сегодняшний момент, несмотря на использование более сложных схем, данный термин все имеет широкое применение.
Если сложение, очевидно, не пригодно для формирования эффективной контрольной суммы, то таким действием вполне может оказаться деление при условии, что делитель имеет ширину регистра контрольной суммы.
Основная идея алгоритма CRC состоит в представлении сообщения виде огромного двоичного числа, делении его на другое фиксированное двоичное число и использовании остатка этого деления в качестве контрольной суммы. Получив сообщение, приемник может выполнить аналогичное действие и сравнить полученный остаток с "контрольной суммой" (переданным остатком).
Пример:
Предположим, что сообщение состоит из 2 байт (6, 23), как и в предыдущем примере. Их можно рассматривать, как шестнадцатеричное число 0167h, или как двоичное число 0000 0110 0001 0111. Предположим, что ширина регистра контрольной суммы составляет 1 байт, а в качестве делителя используется 1001, тогда сама контрольная сумма будет равна остатку от деления 0000 0110 0001 0111 на 1001. Хотя в данной ситуации деление может быть выполнено с использованием стандартных 32 битных регистров, в общем случае это не верно. Поэтому воспользуемся делением "в столбик". Только на этот раз, оно будет выполняться в двоичной системе счисления:
...0000010101101 = 00AD = 173 =
----_---_---_---_
9= 1001 ) 0000011000010111 = 0617 = 1559 =
0000.,,....,.,,,
----.,,....,.,,,
0000,,....,.,,,
0000,,....,.,,,
----,,....,.,,,
0001,....,.,,,
0000,....,.,,,
----,....,.,,,
0011....,.,,,
0000....,.,,,
----....,.,,,
0110...,.,,,
0000...,.,,,
----...,.,,,
1100..,.,,,
1001..,.,,,
====..,.,,,
0110.,.,,,
0000.,.,,,
----.,.,,,
1100,.,,,
1001,.,,,
====,.,,,
0111.,,,
0000.,,,
----.,,,
1110,,,
1001,,,
====,,,
1011,,
1001,,
====,,
0101,
0000,
----
1011
1001
====
0010 = 02 = 2
В десятичном виде это будет звучать так: "частное от деления 1559 на 9 равно 173 и 2 в остатке".
Хотя влияние каждого бита исходного сообщения на частное не столь существенно, однако 4 битный остаток во время вычислений может радикально измениться, и чем больше байтов имеется в исходной сообщении (в делимом), тем сильнее меняется каждый раз величина остатка. Вот почему деление оказывается применимым там, где обычное сложение работать отказывается.
В нашем случае передача сообщения вместе с 4 битной контрольной суммой выглядела бы (в шестнадцатеричном виде) следующим образом: 06172, где 0617 – это само сообщение, а 2 – контрольная сумма. Приемник, получив сообщение, мог бы выполнить аналогичное деление и проверить, равен ли остаток переданному значению (2).
Хотя арифметическое деление, описанное выше, очень похоже на схему расчета контрольной суммы, называемой CRC, сам же алгоритм CRC несколько более сложен, и, чтобы понять его, необходимо окунуться в теорию целых чисел.
Полином (Polynomial) – Полином является делителем CRC алгоритма.
Все CRC алгоритмы основаны на полиномиальных вычислениях, и для любого алгоритма CRC можно указать, какой полином он использует.
Вместо представления делителя, делимого (сообщения), частного и остатка в виде положительных целых чисел можно представить их в виде полиномов с двоичными коэффициентами или в виде строки бит, каждый из которых является коэффициентом полинома. Например, десятичное число 23 в шестнадцатеричной системе счисления имеет вид 17, а в двоичном – 10111, что совпадает с полиномом:
1*x^4 + 0*x^3 + 1*x^2 + 1*x^1 + 1*x^0
или, упрощенно:
x^4 + x^2 + x^1 + x^0
И сообщение, и делитель могут быть представлены в виде полиномов, с которыми как и раньше можно выполнять любые арифметические действия. Предположим, что хотим перемножить, например, 1101 и 1011. Это можно выполнить, как умножение полиномов:
(x^3 + x^2 + x^0)(x^3 + x^1 + x^0)
= (x^6 + x^4 + x^3
+ x^5 + x^3 + x^2
+ x^3 + x^1 + x^0) = x^6 + x^5 + x^4 + 3*x^3 + x^2 + x^1 + x^0
Теперь для получения правильного ответа необходимо указать, что Х равен 2, и выполнить перенос бита от члена 3*x^3.
В результате получим:
x^7 + x^3 + x^2 + x^1 + x^0
Все это очень похоже на обычную арифметику, с той лишь разницей, что основание у нас лишь предполагается, а не строго задано. Если "X" неизвестен, то не можем выполнить перенос. Неизвестно, что 3*x^3 – это то же самое, что и x^4 + x^3, так как не знаем, что X=2. В полиномиальной арифметике связи между коэффициентами не установлены, и, поэтому, коэффициенты при каждом члене полинома становятся строго типизированными — коэффициент при x^2 имеет иной тип, чем при x^3.
Если коэффициенты каждого члена полинома совершенно изолированы друг от друга, то можно работать с любыми видами полиномиальной арифметики, просто меняя правила, по которым коэффициенты работают. Одна из таких схем для нас чрезвычайно интересна, а именно, когда коэффициенты складываются по модулю 2 без переноса – то есть коэффициенты могут иметь значения лишь 0 или 1, перенос не учитывается. Это называется "полиномиальная арифметика по модулю 2".
Возвращаясь к предыдущему примеру:
(x^3 + x^2 + x^0)(x^3 + x^1 + x^0)
= (x^6 + x^4 + x^3
+ x^5 + x^3 + x^2
+ x^3 + x^1 + x^0)
= x^6 + x^5 + x^4 + 3*x^3 + x^2 + x^1 + x^0
По правилам обычной арифметики, коэффициент члена 3*x^3 распределяется по другим членам полинома, используя механизм переноса и предполагая, что X = 2. В "полиномиальной арифметике по модулю 2" не известно, чему равен "X", переносов здесь не существует, а все коэффициенты рассчитываются по модулю 2. В результате получаем:
= x^6 + x^5 + x^4 + x^3 + x^2 + x^1 + x^0
Таким образом, полиномиальная арифметика по модулю 2 – это фактически двоичная арифметика по модулю 2 без учета переносов. Хотя полиномы имеют удобные математические средства для анализа CRC алгоритмов и алгоритмов коррекции ошибок, для упрощения дальнейшего обсуждения они будут заменены, на непосредственные арифметические действия в системе, с которой они изоморфны, а именно в системе двоичной арифметики без переносов.
Двоичная арифметика без учета переносов
Оставим полиномы вне поля нашего внимания, и сфокусируем его на обычной арифметике, так как действия, выполняемые во время вычисления CRC, являются арифметическими операциями без учета переносов. Эта арифметическая система является ключевой частью расчетов CRC.
Сложение двух чисел в CRC арифметике полностью аналогично обычному арифметическому действию за исключением отсутствия переносов из разряда в разряд. Это означает, что каждая пара битов определяет результат своего разряда вне зависимости от результатов других пар. Например:
10011011
+11001010
--------
01010001
Для каждой пары битов возможны 4 варианта:
0+0=0
0+1=1
1+0=1
1+1=0 ( )
То же самое справедливо и для вычитания:
10011011
-11001010
--------
01010001
когда имеются также 4 возможные комбинации:
0-0=0
0-1=1 ( )
1-0=1
1-1=0
Фактически, как операция сложения, так и операция вычитания в CRC арифметике идентичны операции "Исключающее ИЛИ" (eXclusive OR – XOR), что позволяет заменить 2 операции первого уровня (сложение и вычитание) одним действием, которое, одновременно, оказывается инверсным самому себе. Очень удобное свойство такой арифметики.
Сгруппировав сложение и вычитание в одно единое действие, CRC арифметика исключает из поля своего внимания все величины, лежащие за пределами самого старшего своего бита. Хотя совершенно ясно, что значение 1010 больше, чем 10, это оказывается не так, когда говорят, что 1010 должно быть больше, чем 1001.
Чтобы понять почему, попытайтесь получить из 1010 значение 1001, отняв или прибавив к нему одну и ту же величину:
1001 = 1010 + 0011
1001 = 1010 – 0011
Это сводит на нет всякое представление о порядке. Определив действие сложения, перейдем к умножению и делению. Умножение, как и в обычной арифметике, считается суммой значений первого сомножителя, сдвинутых в соответствии со значением второго сомножителя.
1101x
1011
----
1101
1101.
0000..
1101...
-------
1111111
Обратим внимание: при суммировании используется CRC сложение.
Деление несколько сложнее, так как требуется знать, когда "одно число превращается в другое ". Чтобы сделать это, необходимо ввести слабое понятие размерности: число X больше или равно Y, если позиция самого старшего единичного бита числа X более значима (или соответствует) позиции самого старшего единичного бита числа Y. Ниже приведен пример деления:
1100001010
————————————————
10011 ) 11010110110000
10011,,.,,....
-----,,.,,....
10011,.,,....
10011,.,,....
-----,.,,....
00001.,,....
00000.,,....
-----.,,....
00010,,....
00000,,....
-----,,....
00101,....
00000,....
-----,....
01011....
00000....
-----....
10110...
10011...
-----...
01010..
00000..
-----..
10100.
10011.
-----.
01110
00000
-----
1110 =
Это так и есть. Однако, прежде, чем идти дальше, стоит еще немного задержаться на этих действиях.
Зная, что действия сложения и вычитания в нашей арифметике – это одно и то же. В таком случае, A+0=A и A-0=A.
Если число A получено умножением числа B, то в CRC арифметике это означает, что существует возможность сконструировать число A из нуля, применяя операцию XOR к числу B, сдвинутому, на различное количество позиций. Например, если A равно 0111010110, а B – 11, то может сконструировать A из B следующим способом:
0111010110
= .......11.
+ ....11....
+ ...11.....
11.......
Однако, если бы A было бы равно 0111010111, то не удалось составить его с помощью различных сдвигов числа поэтому говорят, что в CRC арифметике оно не делится на B.
Таким образом, видно, что CRC арифметика сводится главным образом к операции "Исключающее ИЛИ" некоторого значения при различных величинах сдвига.
Определив все правила CRC арифметики, можно теперь охарактеризовать вычисление CRC как простое деление, чем оно фактически и является. Чтобы выполнить вычисление CRC, необходимо выбрать делитель. Говоря математическим языком, делитель называется генераторным полиномом (generator polinomial), или просто полиномом, и это ключевое слово любого CRC алгоритма. Для простоты будет называть CRC полином просто полиномом. Можно выбрать и использовать в CRC любой полином. Степень полинома W (Width – ширина) (позиция самого старшего единичного бита) чрезвычайно важна, так как от нее зависят все остальные расчеты. Обычно выбирается степень 16 ил 32, так как это облегчает реализацию алгоритма на со временных компьютерах. Степень полинома – это действительная позиция старшего бита, например, степень полинома 10011 равна 4, а не 5.
Степень (Width) – Степень (или ширина) CRC алгоритма соответствует степе ни используемого полинома (или длине полинома минус единица). Например, если используется полином 11010, то степень алгоритма равна 4. Обычно используется степень, кратная 8
Выбрав полином приступим к расчетам. Это будет простое деление (в терминах CRC арифметики) сообщения на наш полином. Единственное, что надо будет сделать до начала работы, так это дополнить сообщение W нулевыми битами. Итак, начнем.
Исходное сообщение: 1101011011
Полином: 10011
Сообщение, дополненное W битами: 11010110110000
Теперь просто поделим сообщение на полином, используя правила CRC арифметики. Ранее уже рассматривалось это действие.
1100001010 = ( )
---------------
10011 ) 11010110110000 = выровненное сообщение (1101011011 + 0000)
=# ,,.,.,,.,,....
10011,,.,,....
-----,,.,,....
10011,.,,....
10011,.,,....
-----,.,,....
00001.,,....
00000.,,....
-----.,,....
00010,,....
00000,,....
-----,,....
00101,....
00000,....
-----,....
01011....
00000....
-----....
10110...
10011...
-----...
01010..
00000..
-----..
10100.
10011.
-----.
01110
00000
-----
1110
В результате получаем частное, которое нас не интересует и, поэтому, отбрасывается за ненадобностью, и остаток, который и используется в качестве контрольной суммы. Расчет закончен. Как правило, контрольная сумма добавляется к сообщению и вместе с ним передается по каналам связи. В нашем случае будет передано следующее сообщение:
11010110111110
На другом конце канала приемник может сделать одно из равноценных действий:
1. Выделить текст собственно сообщения, вычислить для него контрольную сумму (не забыв при этом дополнить сообщение W битами), и сравнить ее с переданной.
2. Вычислить контрольную сумму для всего переданного сообщения (без добавления нулей), и посмотреть, получится ли в результате нулевой остаток.
Оба эти варианта совершенно равноправны.
Таким образом, при вычислении CRC необходимо выполнить следующие действия:
1. Выбрать степень полинома W и полином G (степени W).
2. Добавить к сообщению W нулевых битов. Назовем полученную строку M'.
3. Поделим M' на G с использованием правил CRC арифметики. Полученный остаток и будет контрольной суммой.
Надо отметить, что переданное сообщение T является произведением полинома. Чтобы понять это, обратите внимание, что 1) последние W бит сообщения – это остаток от деления дополненного нулями исходного сообщения на выбранный полином, и 2) сложение равносильно вычитанию, поэтому прибавление остатка дополняет значение сообщения до следующего полного произведения. Теперь смотрите, если сообщение при передаче было повреждено, то получим со общение T E, где E – это вектор ошибки, а ' ' – это CRC сложение (или операция XOR). Получив сообщение, приемник делит T E на G. Так как T mod G = 0, (T E) mod G = E mod G. Следовательно, качество полинома, который выбираем для перехвата некоторых определенных видов ошибок, будет определяться набором произведений G, так как в случае, когда E также является произведением G, такая ошибка выявлена не будет. Следовательно, наша задача состоит в том, чтобы найти такие классы G, произведения которых будут как можно меньше похожи на шумы в канале передачи (которые и вызывают повреждение сообщения). Рассмотрим, какие типы шумов в канале передачи можем ожидать.
Однобитовые ошибки. Ошибка такого рода означает, что E=1000...0000. Можем гарантировать, что ошибки этого класса всегда будет распознаны при условии, что в G по крайней мере 2 бита установлены в "1". Любое произведение G может быть сконструировано операциями сдвига и сложения, и, в тоже время, невозможно получить значение с 1 единичным битом сдвигая и складывая величину, имеющую более 1 единичного бита, так как в результате всегда будет присутствовать по крайней мере 2 бита.
Двух битовые ошибки. Для обнаружения любых ошибок вида 100...000100...000 (то есть когда E содержит по крайней мере 2 единичных бита) необходимо выбрать такое G, которые бы не имело множителей 11, 101, 1001, 10001, и так далее. Такие полиномы должны существовать - полином с единичными битами в позициях 15, 14 и 1, который не может быть делителем ни одно числа меньше 1...1, где «...» 32767 нулей.
Ошибки с нечетным количеством бит. Может перехватить любые повреждения, когда E имеет нечетное число бит, выбрав полином G таким, чтобы он имел четное количество бит. 1) CRC умножение является простой операцией XOR постоянного регистрового значения с различными смещениями; 2) XOR – это всего-навсего операция переключения битов; и 3) если применяется в регистре операция XOR к величине с четным числом битов, четность количества единичные битов в регистре останется неизменной. На пример, начнем с E=111 и попытаемся сбросить все 3 бита в "0" последовательным выполнением операции XOR с величиной 11 и одним из 2 вариантов сдвигов (то есть, "E=E XOR 011" и "E=E XOR 110"). Это аналогично задаче о перевертывании стаканов, когда за одно действие можно перевернуть одновременно любые два стакана. Большинство популярных CRC полиномов содержат четное количество единичных битов.
Пакетные ошибки. Пакетная ошибка выглядит как E=000...000111...11110000...00, то есть E состоит из нулей за исключением группы единиц где то в середине. Эту величину можно преобразовать в E=(10000...00)(1111111...111), где имеется z нулей в левой части и n единиц в правой. Для выявления этих ошибок необходимо установить младший бит G в 1. При этом необходимо, чтобы левая часть не была множителем G. При этом всегда, пока G шире правой части, ошибка всегда будет распознана.
Вот несколько популярных полиномов:
16 битные: (16,12,5,0) [стандарт «X25»]
(16,15,2,0) ["CRC 16"]
32 битные: (32,26,23,22,16,12,11,10,8,7,5,4,2,1,0) [Ethernet]
1.3 Код Хэмминга
Предположим, что слово состоит из m битов данных, к которым прибавляем г дополнительных битов (контрольных разрядов). Пусть общая длина слова будет n (то есть n-m+г). п-битную единицу, содержащую m битов данных и г контрольных разрядов, часто называют кодированным словом. Для любых двух кодированных слов, например 10001001 и 10110001, можно определить, сколько соответствующих битов в них различается. В данном примере таких бита три. Чтобы определить количество различающихся битов, нужно над двумя кодированными словами произвести логическую операцию ИСКЛЮЧАЮЩЕЕ ИЛИ и сосчитать число битов со значением 1 в полученном результате. Число битовых позиций, по которым различаются два слова, называется интервалом Хэмминга. Если интервал Хэмминга для двух слов равен d, это значит, что достаточно d битовых ошибок, чтобы превратить одно слово в другое. Например, интервал Хэмминга кодированных слов 11110001 и 00110000 равен 3, поскольку для превращения первого слова во второе достаточно 3 ошибок в битах. Память состоит из m-битных слов, и следовательно, существует 2m вариантов сочетания битов. Кодированные слова состоят из n битов, но из-за способа подсчета контрольных разрядов допустимы только 2т из 2" кодированных слов. Если в памяти обнаруживается недопустимое кодированное слово, компьютер знает, что произошла ошибка. При наличии алгоритма для подсчета контрольных разрядов можно составить полный список допустимых кодированных слов и из этого списка найти два слова, для которых интервал Хэмминга будет минимальным. Это интервал Хэмминга полного кода. Свойства проверки и исправления ошибок определенного кода зависят от его интервала Хэмминга. .Чтобы обнаружить d ошибок в битах, необходим код с интервалом d+1, поскольку d ошибок не могут изменить одно допустимое кодированное слово на другое допустимое кодированное слово. Соответственно, чтобы исправить d ошибок в битах, необходим код с интервалом 2d+l, поскольку в этом случае допустимые кодированные слова так сильно отличаются друг от друга, что даже если произойдет d изменений, изначальное кодированное слово будет ближе к ошибочному, чем любое другое кодированное слово, поэтому его без труда можно будет определить.
В качестве простого примера кода с обнаружением ошибок рассмотрим код, в котором к данным присоединяется один бит четности. Бит четности выбирается таким образом, что число битов со значением 1 в кодированном слове четное (или нечетное). Интервал этого кода равен 2, поскольку любая ошибка в битах приводит к кодированному слову с неправильной четностью. Другими словами, достаточно двух ошибок в битах для перехода от одного допустимого кодированного слова к другому допустимому слову. Такой код может использоваться для обнаружения одиночных ошибок. Если из памяти считывается слово, содержащее неверную четность, поступает сигнал об ошибке. Программа не сможет продолжаться, но зато не будет неверных результатов.
В качестве простого примера кода с исправлением ошибок рассмотрим код с четырьмя допустимыми кодированными словами:
0000000000, 0000011111, 1111100000 и 1111111111
Интервал этого кода равен 5. Это значит, что он может исправлять двойные ошибки. Если появляется кодированное слово 0000000111, компьютер знает, что изначальное слово должно быть 0000011111 (если произошло не более двух ошибок). При наличии трех ошибок, если, например, слово 0000000000 изменилось на 0000000111, этот метод недопустим. Представим, что хотим разработать код с m битами данных и г контрольных разрядов, который позволил бы исправлять все ошибки в битах. Каждое из 2r допустимых слов имеет n недопустимых кодированных слов, которые отличаются от допустимого одним битом. Они образуются инвертированием каждого из n битов в n-битном кодированном слове. Следовательно, каждое из 2r допустимых слов требует п+1 возможных сочетаний битов, приписываемых этому слову (п возможных ошибочных вариантов и один правильный). Поскольку общее число различных сочетаний битов равно 2n, то (n+l)2m<2n.
Так как n=m+r, следовательно, (m+r+1)<2г. Эта формула дает нижний предел числа контрольных разрядов, необходимых для исправления одиночных ошибок. В табл. 1.1 показано необходимое количество контрольных разрядов для слов разного размера.
Табл.1.1 — Размерность кода
| Размер слова | Кол-во контроль разрядов | Общий размер | % увеличения длины слова |
| 8 16 32 64 128 256 512 | 4 5 6 7 8 9 10 | 12 21 38 71 136 265 522 | 50 31 19 11 6 4 2 |
Этого теоретического нижнего предела можно достичь, используя метод Ричарда Хэмминга. В коде Хэмминга к слову, состоящему из m битов, добавляется r битов четности, при этом образуется слово длиной m+r битов. Биты нумеруются с единицы (а не с нуля), причем первым считается крайний левый. Все биты, номера которых — степени двойки, являются битами четности; остальные используются для данных. Например, к 16-битному слову нужно добавить 5 битов четности. Биты с номерами 1, 2, 4, 8 и 16 — биты четности, а все остальные — биты данных. Всего слово содержит 21 бит (16 битов данных и 5 битов четности). В рассматриваемом примере будем использовать положительную четность (выбор произвольный). Каждый бит четности проверяет определенные битовые позиции. Общее число битов со значением 1 в проверяемых позициях должно быть четным. Ниже указаны позиции проверки для каждого бита четности:
Бит 1 проверяет биты 1,3,5,7,9,11,13,15,17,19,21.
Бит 2 проверяет биты 2,3,6,7,10, 11, 14,15,18,19.
Бит 4 проверяет биты 4,5,6,7,12,13,14,15,20,21.
Бит 8 проверяет биты 8,9, 10, 11,12,13,14,15.
Бит 16 проверяет биты 16,17,18,19,20,21.
В общем случае бит b проверяется битами b1, b2,..., bj, такими что b1+b2+...+bj=b.
Например, бит 5 проверяется битами 1 и 4, поскольку 1+4-5. Бит 6 проверяется битами 2 и 4, поскольку 2+4=6 и т. д.
На рис. 1.3 показано построение кода Хэмминга для 16-битного слова 1111000010101110. Соответствующим 21-битным кодированным словом является 001011 100000101101110. Чтобы увидеть, как происходит исправление ошибок, рассмотрим, что произойдет, если бит 5 изменит значение из-за резкого скачка напряжения на линии электропередачи. В результате вместо кодированного слова 001011100000101101110 получится 001001100000101101110. Будут проверены 5 битов четности. Вот результаты проверки:
Бит четности 1 неправильный (биты 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 содержат пять единиц).
Бит четности 2 правильный (биты 2,3,6,7,10,11,14,15,18,19 содержат шесть единиц).
Бит четности 4 неправильный (биты 4,5,6,7,12,13,14,15,20,21 содержат пять единиц).
Бит четности 8 правильный (биты 8,9,10,11,12,13,14,15 содержат две единицы).
Бит четности 16 правильный (биты 16,17,18,19,20,21 содержат четыре единицы).
Общее число единиц в битах 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 и 21 должно быть четным, поскольку в данном случае используется положительная четность. Неправильным должен быть один из битов, проверяемых битом четности 1 (а именно 1,3,5,7,9,11,13,15,17,19 и 21). Бит четности 4 тоже неправильный. Это значит, что изменил значение один из следующих битов: 4,5,6,7,12,13,14,15,20,21. Ошибка должна быть в бите, который содержится в обоих списках. В данном случае общими являются биты 5,7,13,15 и 21. Поскольку бит четности 2 правильный, биты 7 и 15 исключаются. Правильность бита четности 8 исключает наличие ошибки в бите 13. Наконец, бит 21 также исключается, поскольку бит четности 16 правильный. В итоге остается бит 5, в котором и содержится ошибка. Поскольку этот бит имеет значение 1, он должен принять значение 0. Именно таким образом исправляются ошибки.
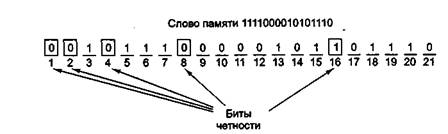
Рис. 1.3 — Построение кода Хэмминга для слова 1111000010101110с помощью добавления 5 контрольных разрядов к битам данных
Чтобы найти неправильный бит, сначала нужно подсчитать все биты четности. Если они правильные, ошибки нет (или есть, но больше одной). Если обнаружились неправильные биты четности, то нужно сложить их номера. Сумма, полученная в результате, даст номер позиции неправильного бита. Например, если биты четности 1 и 4 неправильные, а 2, 8 и 16 правильные, то ошибка произошла в бите 5 (1+4)
Похожие работы
... , работавших в области электротехники, заинтересовалась возможностью создания технологии хранения данных, обеспечивающей более экономное расходование пространства. Одним из них был Клод Элвуд Шеннон, основоположник современной теории информации. Из разработок того времени позже практическое применение нашли алгоритмы сжатия Хаффмана и Шеннона-Фано. А в 1977 г. математики Якоб Зив и Абрахам Лемпел ...
... за которым следует устройство дискретизации (рисунок 4.2), подастся известный сигнал s(t) плюс шум AWGN n(t). 4.4 Межсимвольная интерференция На рисунке 4.3 а) представлены фильтрующие элементы типичной системы цифровой связи. В системе - передатчике, приемнике и канале - используется множество разнообразных фильтров (и реактивных элементов, таких как емкость и индуктивность). В передатчике ...
... ? 8. Какими программами можно воспользоваться для устранения проблем и ошибок, обнаруженных программой Sandra? Раздел 3. Автономная и комплексная проверка функционирования и диагностика СВТ, АПС и АПК Некоторые из достаточно интеллектуальных средств вычислительной техники, такие как принтеры, плоттеры, могут иметь режимы автономного тестировании. Так, автономный тест принтера запускается без ...
... и сеть Internet. АПЗ.38.098424.003 ПЗ Изм Лит № докум Подпись Дата МНОГОФУНКЦИОНАЛЬНЫЙ КОНТРОЛЛЕР ВЗУ Пояснительная записка Лит Лист Листов Разраб Борщ С. К 2 20 Провер Скороделов В. ...



0 комментариев